【机器人-基础知识】标定 - IMU（Inertial Measurement Unit, 惯性测量单元）

1. IMU的输出内容

IMU（惯性测量单元）的输出主要包括以下几类信号：

• 加速度数据
  三轴加速度计输出沿 X、Y、Z 轴方向的线性加速度，这些数据反映了物体受到的重力及运动加速度。

• 角速度数据
  三轴陀螺仪输出绕 X、Y、Z 轴的角速度，描述了物体的旋转情况。

• 磁场数据（视具体型号而定）
  如果IMU内集成了磁力计，则还会输出三轴磁场数据，用于辅助判断绝对方向和校正姿态漂移。

• 温度数据（部分型号）
  某些IMU会提供内部温度信息，以便进行温度补偿和噪声分析。

此外，经过传感器融合算法处理后，部分系统还可以直接输出估计的姿态信息，但这些是基于原始传感器数据进一步计算得到的结果.

2. 主要组成部件

1. 加速度计
   测量物体在三个正交轴上的线性加速度。内部通常有一个微小的“惯性块”（proof mass），当设备受到加速度作用时，该惯性块相对于外壳产生位移，通过检测这种位移来计算加速度。

2. 陀螺仪
   测量物体绕各轴的角速度。现代IMU大多采用MEMS陀螺仪，利用科氏效应（Coriolis Effect）：当一个振动元件在旋转系统中运动时，科氏力会使其振动方向发生偏转，通过检测这种偏转就能计算出旋转速度。

3. 磁力计（有时集成）
   用于测量地磁场方向，辅助确定设备的绝对朝向，尤其在GPS信号弱或无GPS时提供方位参考。

3. IMU组成部件工作原理

3.1. 加速度计

1. 加速度计的底层工作原理

加速度计的底层原理还是牛顿第二定律：物体的加速度与施加到该物体上的力成正比，即 $F=ma$.

2. 加速度计的常见类型

加速度计类型	主要特点	工作原理	应用场景/优缺点
MEMS加速度计	小型、低功耗、成本低	利用微机械结构中悬挂的惯性块在受加速度作用下发生位移，导致电容变化，转换为电压信号	广泛用于智能手机、无人机、机器人等消费级和工业级IMU；静态和动态测量均适用
压电加速度计	高频响应快，适合动态测量	利用压电材料在受力时产生电荷信号，通过电荷放大后输出与加速度成比例的信号	适用于高频振动和冲击测量，但对直流（静态）加速度不敏感
压阻加速度计	结构简单、制造成熟	基于半导体应变片受力时电阻发生变化，通过惠斯登电桥检测电阻变化转换为电压信号	精度要求适中，但温度敏感；在一些特殊场合也有应用

3.2. 陀螺仪

1. 陀螺仪的底层原理

陀螺仪的底层原理主要依赖于两个核心物理效应：

1. 角动量守恒原理（传统机械陀螺仪）：
   在传统机械陀螺仪中，一个高速旋转的转子具有很大的角动量。根据角动量守恒定律，这个转子在没有外力矩作用下会保持其旋转轴方向不变。当陀螺仪本体发生旋转时，由于转子倾向于维持原有的旋转状态，其偏离会产生“进动”现象，通过检测这种进动现象，就可以推断出旋转的角速度和方向。

2. 科氏效应（MEMS陀螺仪）：
   现代多数IMU采用的MEMS陀螺仪，其工作原理基于科氏效应。MEMS陀螺仪中通常有一个振动的微机械结构，当设备发生旋转时，振动体在运动过程中会受到一个垂直于原始振动方向的科氏力，该力的大小与旋转角速度成正比。通过检测这种由科氏力引起的微小振动（通常通过电容、压阻或其他传感方式感知），便能计算出设备的角速度。

2. 进动现象

a. 进动现象 (旋进现象)原理

进动：当陀螺仪本体受到外部力矩时，转子因其较大的角动量倾向于维持原来的自旋状态，结果并不是直接沿力矩方向转动，而是在垂直于自旋轴和外力矩方向上发生缓慢的转动。

当转子自旋角动量 $\vec{L}$ 很大时，外力矩主要改变的是 $\vec{L}$ 的方向而非大小，从而产生进动。进动角速度 ${\vec{\Omega }}_p$ 满足：

$${\vec{\Omega }}_p\times \vec{L}=\vec{M}$$

取模后得：

$${\Omega }_p=\frac{M}{|\vec{L}|}$$

其中，转子的角动量 $|\vec{L}|$ 通常由转子转动惯量 $I$ 与自旋角速度 ${\omega }_s$ 决定，即：

$$|\vec{L}|=I{\omega }_s$$

代入上式可得：

$${\Omega }_p=\frac{M}{|\vec{L}|}=\frac{M}{I{\omega }_s}$$

• 在外部力矩 $M$ 和转子转动惯量 $I$ 固定的情况下，进动角速度 ${\Omega }_p$ 与自转角速度 ${\omega }_s$ 成反比关系。
• 即当自转角速度增大时，进动角速度会减小；反之，当自转角速度减小时，进动角速度增大。

---

b. 推导陀螺仪本体的旋转角速度

• 预先使转子以稳定且较高的自旋角速度旋转，这通常由电机控制，并且该自旋角速度 ${\omega }_s$ 被设计为一个已知且恒定的值。

• 当陀螺仪本体（安装在外壳上）发生旋转时，外部施加的旋转角速度 $\vec{\omega }$ 会在转子上产生一个力矩，转子受到的力矩为
  $$\vec{M}=\vec{\omega }\times \vec{L}$$

• 等效力矩
  当陀螺仪的外壳以角速度 $\vec{\omega }$ 旋转时，虽然没有施加传统意义上的“力”，但转子却处于一个非惯性（旋转）参考系中。
  在这种情况下，角动量向量 $\vec{L}$ 会因为参考系的旋转而发生改变，数学上描述为：
  $$\frac{d\vec{L}}{dt}=\vec{\omega }\times \vec{L}$$
  这个方程说明，即使在没有“真实”外力矩的情况下，旋转参考系会引入一个等效的时间变化率，从而表现出一个等效的力矩 ${\vec{\tau }}_{\text{eff}}$：
  $${\vec{\tau }}_{\text{eff}}=\vec{\omega }\times \vec{L}=\vec{M}$$

• 等效力矩的物理意义
  当陀螺仪的外壳旋转时，转子由于其较大的角动量倾向于保持原来的方向（这就是转子“抗拒”改变方向的性质）。而外部旋转则试图改变这种方向，结果在转子上产生了一个反映为进动的现象，这个现象实际上就是上述等效力矩的体现。

• 旋进角速度计算
  将等效力矩代入上式可得：
  $${\Omega }_p=\frac{M}{|\vec{L}|}=\frac{|\vec{\omega }\times \vec{L}|}{I{\omega }_s}$$

• 极端情况分析：如果外壳旋转轴（$\vec{\omega }$的旋转轴）与自旋轴垂直（$\vec{L}$的方向）（最敏感情况），则有 :

$${\Omega }_p=\frac{\omega I{\omega }_s}{I{\omega }_s}=\omega$$
在一般情况下，通过测量进动的分量（利用传感器检测转子因进动产生的偏转），并已知 ${\omega }_s$ 和 $I$，就可以通过上述关系反推外部旋转角速度 $\vec{\omega }$ 的各分量。

• 分解进动分量
  在三轴机械陀螺仪中，通常会通过机械结构或附加传感器（如电位计、光电传感器等）检测转子因进动在设备固定坐标系中的偏转。设检测到的进动角速度在该坐标系中的分量为 ${\Omega }_{px},{\Omega }_{py},{\Omega }_{pz}$。

3. 科氏效应原理解析

a. 理论概述

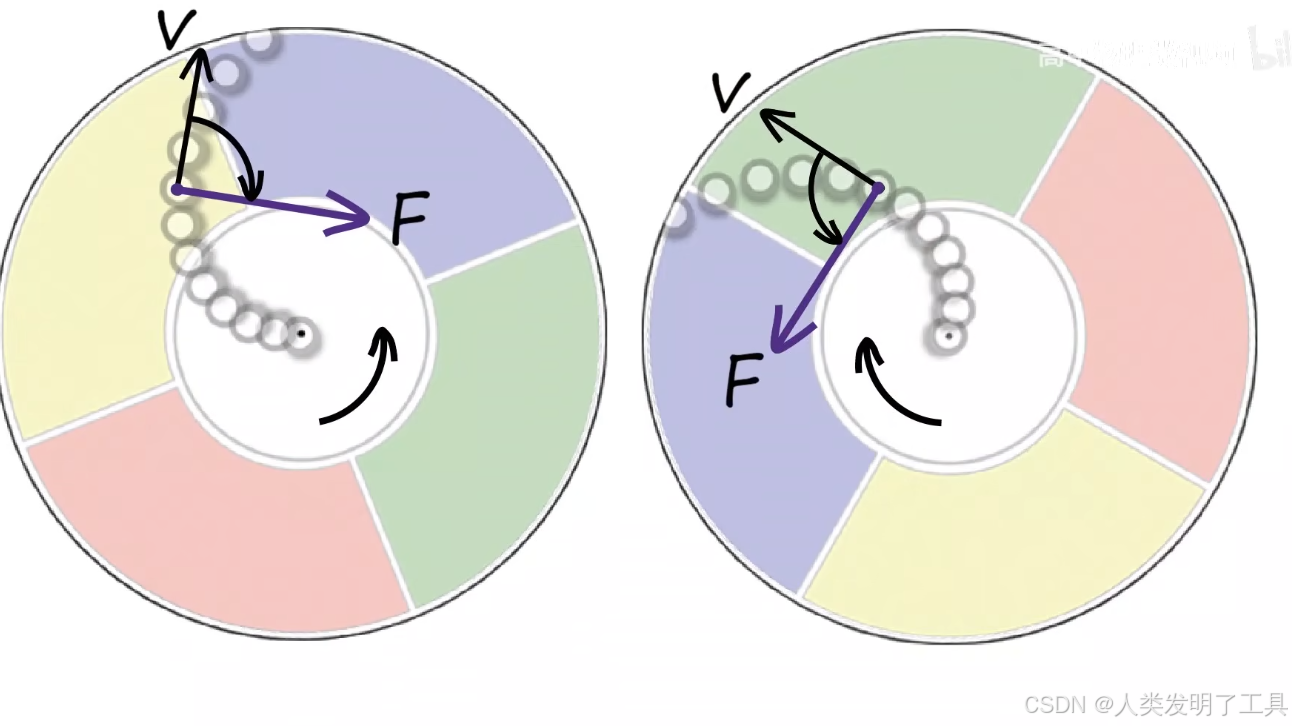
• 旋转参考系中的虚拟力
  当我们处在一个非惯性（旋转）参考系中时，由于参考系自身在旋转，物体的运动轨迹会看起来偏离直线，这种偏离可以用一个虚拟力来解释，这就是科氏力（科里奥利力）。

• 科氏力的物理意义
  科氏力实际上并非真实存在的力，而是由于旋转参考系的加速度所引入的一种惯性效应。它使得在旋转系统内运动的物体，其运动轨迹相对于静止观察者来说发生偏转。

b. 数学描述与公式

在旋转参考系中，假设旋转角速度为 $\vec{\Omega }$，物体质量为 $m$，在该参考系内的速度为 $\vec{v}$。科氏力 ${\vec{F}}_C$ 的公式为：

$${\vec{F}}_C=-2m\vec{\Omega }\times \vec{v}$$

• 符号说明

  • $\vec{\Omega }$：旋转参考系的角速度向量，其方向由右手定则确定。
  • $\vec{v}$：物体在旋转参考系中的速度向量。
  • “$\times$” 表示叉乘，说明科氏力总是垂直于 $\vec{\Omega }$ 和 $\vec{v}$ 两个向量所在的平面。
  • 负号表示科氏力的方向与旋转参考系运动的惯性效应相反。

• 效果
  由于科氏力与物体的运动速度和旋转角速度有关，其大小为：

$$F_C=2m\Omega v\sin \theta$$

其中 $\theta$ 为 $\vec{\Omega }$ 与 $\vec{v}$ 之间的夹角。当 $\vec{\Omega }$ 与 $\vec{v}$ 垂直时，$\sin \theta =1$，科氏力达到最大值。

---

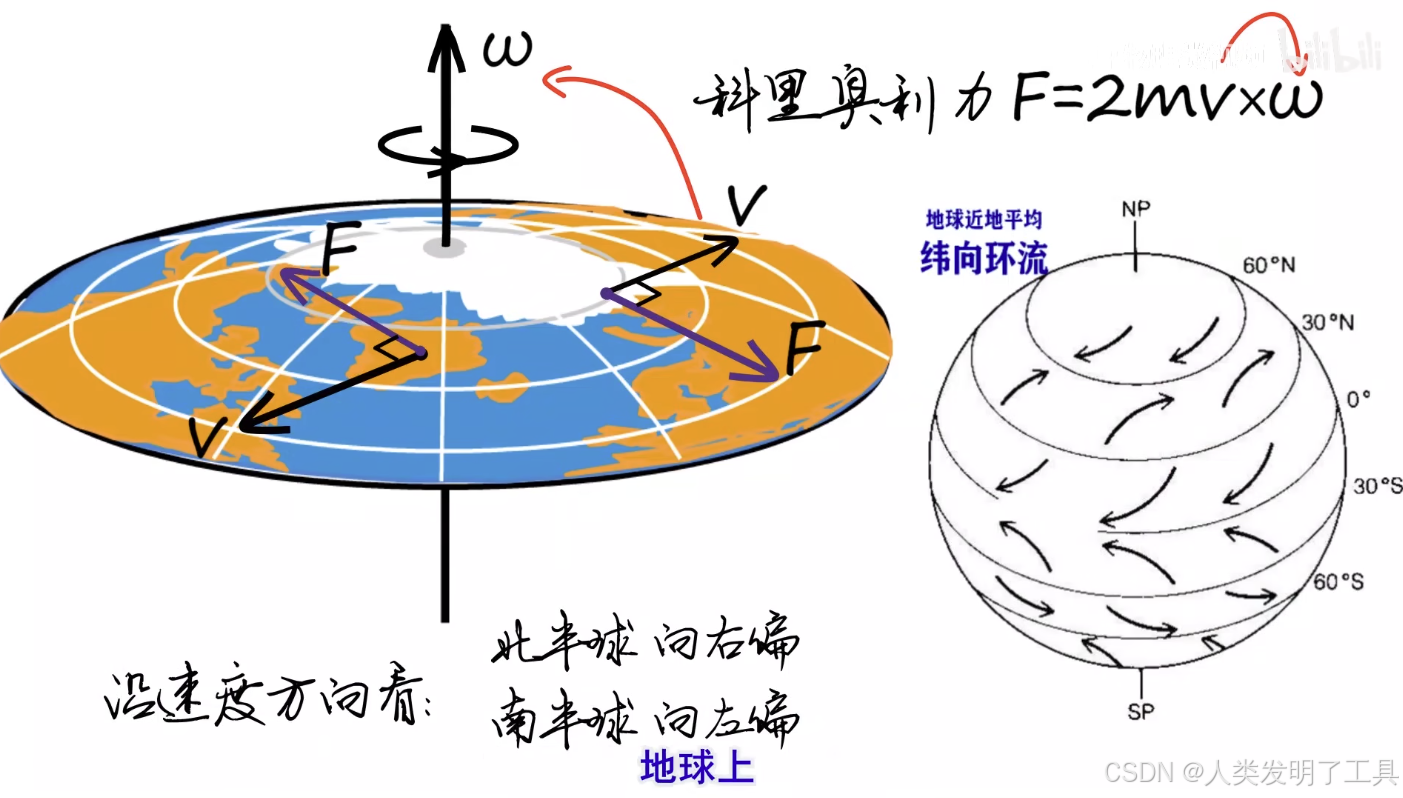
地球上，沿着速度方向看，北半球向右偏，南半球向左偏

c. 示例说明

示例：
设想一个简单的场景：

• 在一个以 $\Omega =1\text{rad/s}$ 旋转的圆盘上，一个质量为 $m=1\text{kg}$ 的物体以 $v=2\text{m/s}$ 在圆盘上沿径向（与旋转轴垂直）运动。
• 因为径向运动与旋转轴正交，所以 $\theta =90^{\circ }$，$\sin \theta =1$。

根据公式，科氏力大小为：

$$F_C=2\times 1\text{kg}\times 1\text{rad/s}\times 2\text{m/s}=4\text{N}$$

4. 陀螺仪的常见类型

陀螺仪类型	主要特点	工作原理	应用场景/优缺点
MEMS陀螺仪	小型、低功耗、成本低、易于集成	利用微机电结构中振动元件的科氏效应检测旋转，输出角速度信号	广泛应用于消费电子、无人机、便携设备；精度受限，存在漂移和噪声问题
光纤陀螺仪（FOG）	高精度、无活动部件、响应快	利用光纤内光束传播的干涉原理，测量旋转引起的光程差产生的相位变化	常用于航空航天、船舶导航等高精度要求场合；成本较高，对环境要求较严格
环形激光陀螺仪（RLG）	精度高、稳定性好	利用激光在封闭环腔内多次反射，通过检测旋转产生的频率差来获得角速率	应用于军用、航空及高端导航系统；体积较大、功耗高、制造成本较高
振动陀螺仪	结构简单、易于制造，介于MEMS和高端陀螺仪之间	利用振动结构（如微振动梁）在旋转时受到科氏力作用，导致振动模式发生变化，从而检测角速度	可用于中高端导航和稳定性要求的场合；精度和稳定性介于MEMS与FOG/RLG之间，可根据设计做适当权衡

5. MEMS陀螺仪工作原理

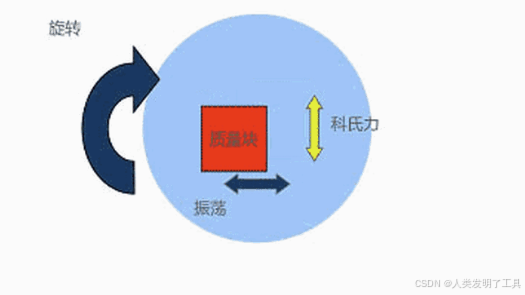
1. 工作原理

在MEMS陀螺仪中，一个微小的振动元件（也称为“检测质量块”）被激励在某一方向（例如 x 轴）振动。当设备绕垂直于该振动方向的轴（例如 z 轴）旋转时，振动质量块会受到一个科氏力的作用，该力的方向与振动方向正交，且与旋转角速度成正比。通过检测这种因科氏力引起的微小位移或应变变化，就可以推算出旋转角速度。

---

2. 基本公式

在旋转情况下，质量块受到的科氏力 ${\vec{F}}_C$ 可由下式描述：

$${\vec{F}}_C=-2m(\vec{\Omega }\times \vec{v})$$

其中：

• $m$ 为质量块的质量
• $\vec{\Omega }$ 为陀螺仪的旋转角速度向量
• $\vec{v}$ 为质量块在检测方向（例如 x 轴）的振动速度
• “$\times$” 表示向量叉乘，负号表示力的方向遵循右手定则（与旋转参考系有关）

如果假设振动仅沿 x 轴进行，且陀螺仪绕 z 轴旋转（角速度为 ${\Omega }_z$），则科氏力在 y 轴上的分量为：
$$F_{C,y}=2m{\Omega }_z{v}_x$$
即
$${\Omega }_z=\frac{F_{C,y}}{2m{v}_x}$$

该力会使质量块在 y 方向产生微小位移，通常通过微电容器或其他敏感元件检测这种位移变化，并转换为电信号输出，与旋转角速度 ${\Omega }_z$ 成正比。

---

3. 示例

假设条件：

• 质量块质量：$m=1\times 10^{-6}\text{kg}$
• 振动速度：$v_x=1\text{m/s}$（这是振动元件在激励状态下的峰值速度）
• 测试旋转角速度：${\Omega }_z=100\text{rad/s}$
• 信号检测科氏力
  当器件绕垂直于振动方向（例如 z 轴）旋转时，科氏力在垂直于振动和旋转轴的方向（例如 y 轴）产生微小位移。这种微小位移通过检测电容变化等方式转换成电信号。
  检测到的科氏力对应的信号转换后相当于 $F_{C,y}=2\times 10^{-4}\text{N}$

信号校准与处理
利用公式
$${\Omega }_z=\frac{F_{C,y}}{2m{v}_x}$$

则旋转角速度计算为：

$${\Omega }_z=\frac{2\times 10^{-4}\text{N}}{2\times 1\times 10^{-6}\text{kg}\times 1\text{m/s}}=100\text{rad/s}$$

检测到的科氏力引起的位移或应变与旋转角速度成正比，经过信号处理后即可输出反映实际旋转角速度的电信号。这个原理使得MEMS陀螺仪能够体积小、功耗低且适合批量生产，广泛应用于惯性导航、姿态控制、消费电子等领域。

4. IMU标定内参和外参

4.1. 标定内容

MEMS 陀螺仪由于制造工艺和环境因素的影响，其输出信号往往包含以下几个误差分量，需要通过标定进行补偿：

• 零偏（Bias）
  静止状态下陀螺仪应输出零角速度，但实际会存在一个固定的偏置。标定时需要测量并去除这种零偏。

• 刻度因数（Scale Factor）
  表示输出信号与实际旋转角速度之间的比例关系。因工艺误差，不同轴的灵敏度可能不一致，需求得准确的比例系数。

• 非正交性（Cross-axis sensitivity / Misalignment）
  理论上三个敏感轴应互相正交，但实际中可能存在一定的夹角误差，导致某一轴受到其他轴信号的干扰。

• 温度效应
  温度变化会引起零偏和刻度因数的漂移，标定时通常需要考虑温度补偿或在恒温条件下进行。

• 噪声特性
  包括角速率随机游走（ARW）、偏置不稳定性等，通过 Allan 方差分析等方法可以对噪声模型进行估计，为后续滤波提供依据。

4.2. 标定方法

1. 内参标定

a. 静态标定

• 原理
  在静止状态下（无外部旋转），理论上陀螺仪输出应为零。通过长时间采集静态数据，可以统计出零偏，并对噪声特性进行分析（例如利用 Allan 方差方法）。

• 步骤

  1. 将陀螺仪放置在静止平台上，在不同温度下分别采集数据。
  2. 对采集数据进行均值计算，得到各轴的静态零偏。
  3. 利用数据方差、Allan 方差等方法分析噪声特性，建立噪声模型。

b. 动态标定

• 原理
  动态标定通常利用已知角速度（如转台旋转、地球自转等参考）来标定刻度因数和非正交性。通过提供一个标准旋转输入，再与陀螺仪输出进行比对，利用优化算法求解各个参数。

• 步骤

  1. 利用转台等装置，在已知角速度下对陀螺仪进行旋转测试。
  2. 收集输出数据，并构建数学模型，如：
     $${\omega }_{\text{meas}}=S\cdot {\omega }_{\text{true}}+b+n,$$
     其中 $S$ 是刻度因数及非正交矩阵，$b$ 是零偏，$n$ 为噪声。
  3. 采用非线性最小二乘法或其他优化算法，最小化测量值与标准角速度之间的误差，从而求解 $S$ 和 $b$。

c. 示例说明

假设：

• 在动态标定中，已知转台旋转角速度为 ${\omega }_{\text{true}}=50\text{rad/s}$
• 采集到的陀螺仪输出为 ${\omega }_{\text{meas}}=[51.2,48.8,50.5]\text{rad/s}$（假设三轴存在零偏和刻度因数误差）

模型构建：
我们假设输出模型为：
$${\omega }_{\text{meas}}=S\cdot {\omega }_{\text{true}}+b$$
其中：

• $S$ 为对角或非对角矩阵（考虑非正交性）
• $b$ 为零偏向量

标定过程：

1. 通过多次旋转测试，收集多组 $\left({\omega }_{\text{true}},{\omega }_{\text{meas}}\right)$ 数据。
2. 构建优化问题，使得误差项
   $$\underset{S,b}{\min }\sum _i\Vert {\omega }_{\text{meas},i}-(S\cdot {\omega }_{\text{true},i}+b){\Vert }^2$$
   达到最小。
3. 求解后，可以得到各轴的刻度因数和零偏，从而将实际测量数据进行补偿，输出准确的旋转角速度。

2. 外参标定

1. 基本原理

IMU 与相机分别建立在不同的坐标系下工作，IMU 测量角速度和加速度，而相机采集图像，通过图像处理可以恢复出相机的位姿（即旋转和平移）。标定问题的目标就是求出二者坐标系之间的刚性变换关系，该关系通常可以表示为一个旋转矩阵 $R$ 和一个平移向量 $\mathbf{t}$。也就是说，对于一个点在 IMU 坐标系中的坐标 ${\mathbf{p}}_{\text{IMU}}$ 与其在相机坐标系中的坐标 ${\mathbf{p}}_{\text{cam}}$，它们满足关系：

$${\mathbf{p}}_{\text{cam}}=R{\mathbf{p}}_{\text{IMU}}+\mathbf{t}$$

2. 公式推导

假设有两个坐标系：

• IMU 坐标系：记为 $I$
• 相机坐标系：记为 $C$

二者之间的刚性变换可写成齐次变换矩阵形式：

$$X=\left[\begin{array}{cc}{R}_{CI}& {\mathbf{t}}_{CI}\\ 0^T& 1\end{array}\right]$$

其中，$R_{CI}$ 表示从 IMU 坐标系到相机坐标系的旋转，${\mathbf{t}}_{CI}$ 表示平移。

对于某个在 IMU 坐标系下的点 ${\mathbf{p}}_I$（在齐次坐标下为 $\left[\begin{array}{c}{\mathbf{p}}_I\\ 1\end{array}\right]$），其在相机坐标系中的表达为：

$$\left[\begin{array}{c}{\mathbf{p}}_C\\ 1\end{array}\right]=X\left[\begin{array}{c}{\mathbf{p}}_I\\ 1\end{array}\right]=\left[\begin{array}{c}{R}_{CI}{\mathbf{p}}_I+{\mathbf{t}}_{CI}\\ 1\end{array}\right]$$

• 基于运动对求解标定参数

在实际标定中，可以利用多个时刻的观测数据来构造方程。假设系统经历了两组运动，对应的 IMU 和相机相对运动分别记为 $B_i$ 和 $A_i$，那么有经典的 Hand-eye 校准模型：

$$A_{i}X=X{B}_i,i=1,2,\dots ,n$$

其中：

• $A_i$ 为相机测量的相对变换（由图像位姿计算得到），形式为：

  $$A_i=\left[\begin{array}{cc}{A}_{iR}& {\mathbf{A}}_{it}\\ 0^T& 1\end{array}\right]$$

• $B_i$ 为 IMU 测量的相对变换（通过积分获得），形式为：

  $$B_i=\left[\begin{array}{cc}{B}_{iR}& {\mathbf{B}}_{it}\\ 0^T& 1\end{array}\right]$$

• $X$ 为从 IMU 到相机的未知变换，即：

  $$X=\left[\begin{array}{cc}{X}_R& X_t\\ 0^T& 1\end{array}\right]$$

该式可以拆分为旋转部分和平移部分：

1. 旋转部分：

   $$A_{iR}{X}_R=X_R{B}_{iR}$$

2. 平移部分：

   $$A_{iR}{X}_t+{\mathbf{A}}_{it}=X_R{\mathbf{B}}_{it}+X_t$$

利用多个运动对，可以使用最小二乘法或其他优化方法来分别求解 $X_R$ 与 $X_t$。

---

3. 分步骤解析

1. 步骤 1：数据采集

• 图像数据：采集一系列图像，通过棋盘格等标定板计算出相机的位姿变化，得到相机相对运动 $A_i$。
• IMU 数据：同时采集 IMU 的加速度与角速度数据，经过积分得到 IMU 相对运动 $B_i$。

2. 步骤 2：数据配对

• 对于每一次运动，提取相机和 IMU 对应时刻的相对变换 $A_i$ 与 $B_i$，要求二者的时间戳同步或者经过时间校准。

3. 步骤 3：旋转矩阵求解

• 利用公式 $A_{iR}{X}_R=X_R{B}_{iR}$ 对所有运动对构建方程组。
• 采用 SVD 分解或其他迭代优化方法求解 $X_R$。

4. 步骤 4：平移向量求解

• 在已知 $X_R$ 的情况下，将平移部分方程

  $$A_{iR}{X}_t+{\mathbf{A}}_{it}=X_R{\mathbf{B}}_{it}+X_t$$

  转化为关于 $X_t$ 的线性方程组，利用最小二乘方法求解。

5. 步骤 5：优化与验证

• 构造整体误差函数（如重投影误差或变换误差），对 $X_R$ 与 $X_t$ 进行全局优化。

• 利用部分数据进行交叉验证，检查求解的标定参数是否满足实际需求。

• 一种构造误差函数的方式是衡量每一对运动对下的残差，即
  $$e_i=A_{i}X-X{B}_i.$$
  由于 $e_i$ 是一个矩阵，我们常用其 Frobenius 范数来衡量误差的大小，整体误差函数可以定义为
  $$E(X)=\sum _{i=1}^n\Vert A_{i}X-X{B}_i{\Vert }_F^2.$$
  最优的 $X$ 应使得 $E(X)$ 尽可能接近零，这表明所求的标定参数能够较好地描述 IMU 与相机之间的转换关系。

---

4. 示例

假设在实验中采集到一组运动数据，得到了以下变换矩阵（为便于理解，此处示例数值简化处理）：

相机的运动变换矩阵 $A_1$

$$A_1=\left[\begin{array}{cccc}0.99& -0.05& 0.10& 0.20\\ 0.06& 0.98& -0.15& 0.10\\ -0.10& 0.16& 0.98& 0.30\\ 0& 0& 0& 1\end{array}\right]$$

IMU 的运动变换矩阵 $B_1$

$$B_1=\left[\begin{array}{cccc}0.98& -0.06& 0.15& 0.18\\ 0.07& 0.97& -0.20& 0.12\\ -0.15& 0.18& 0.96& 0.35\\ 0& 0& 0& 1\end{array}\right]$$

利用多个运动数据构建 $A_{i}X=X{B}_i$ 方程后，通过 SVD 求解得到 IMU 到相机的旋转矩阵和位移向量，例如：

求得的旋转矩阵 $X_R$

$$X_R=\left[\begin{array}{ccc}0.995& -0.030& 0.100\\ 0.040& 0.998& -0.050\\ -0.100& 0.060& 0.993\end{array}\right]$$

求得的平移向量 $X_t$

$$X_t=\left[\begin{array}{c}0.05\\ 0.02\\ 0.10\end{array}\right]$$

因此，IMU 到相机的整体刚性变换矩阵 $X$ 为：

$$X=\left[\begin{array}{cccc}0.995& -0.030& 0.100& 0.05\\ 0.040& 0.998& -0.050& 0.02\\ -0.100& 0.060& 0.993& 0.10\\ 0& 0& 0& 1\end{array}\right]$$

这表示任意一个在 IMU 坐标系下的点 ${\mathbf{p}}_{\text{IMU}}$ 都可以通过

$${\mathbf{p}}_{\text{cam}}=X_R{\mathbf{p}}_{\text{IMU}}+X_t$$

转换到相机坐标系中。