机器学习 单变量线性回归 (2)梯度下降法

一、前言

根据上一篇文章《机器学习 单变量线性回归 (1)背景介绍》中的推理，单元线性回归问题变成了求$w_0$、$w_1$两个变量的值，使得代价函数$J(w_0,w_1)$最小。

梯度下降是一个用来求函数最小值的算法，我们将使用梯度下降算法来求出代价函数$J(w_0,w_1)$的最小值。

二、算法思想

• 存在函数$J(w_0,w_1,\dots ,w_n)$
• 确定$w_0,w_1,\dots ,w_n$的值，使得函数$J$最小

流程：

• 初始化$w_0,w_1,\dots ,w_n$，取任意值即可，如$w_0=0,w_1=0,\dots ,w_n=0$
• 不断改变$w_0,w_1,\dots ,w_n$的值，降低$J(w_0,w_1,\dots ,w_n)$，直到我们找到$J$的全局最小值或局部最小值

为了更加容易理解，我们取n=1，即$J(w_0,w_1)$。$J(w_0,w_1)$函数有两个变量，故此函数图是三维的。假设如下图所示，想象成你站在山上的某个位置（$w_0,w_1$初始值决定的位置），想要尽快走下山（尽快找到$J$的最小值）。

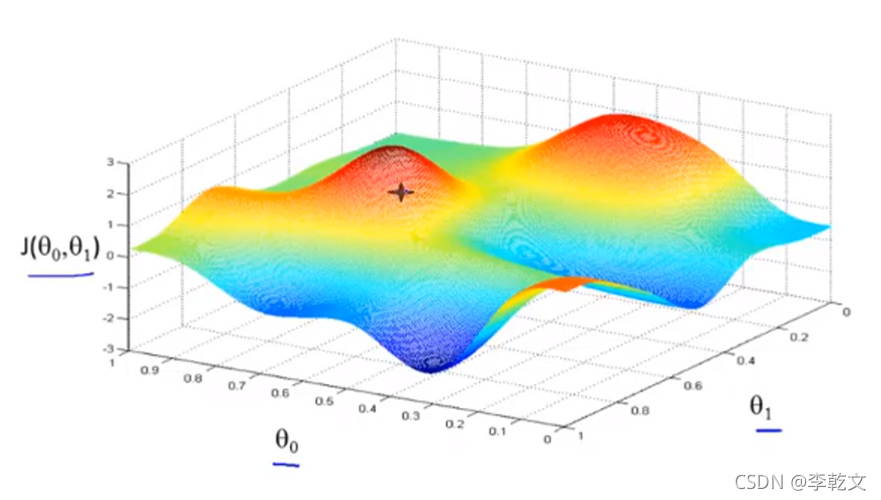
那么你首先会360°观察四周，哪个方向的坡度最陡，然后往前走一段，停下再360°观察四周往最陡的方向走去。。。直到来到一个最低点，四周的坡度都是朝上的了。

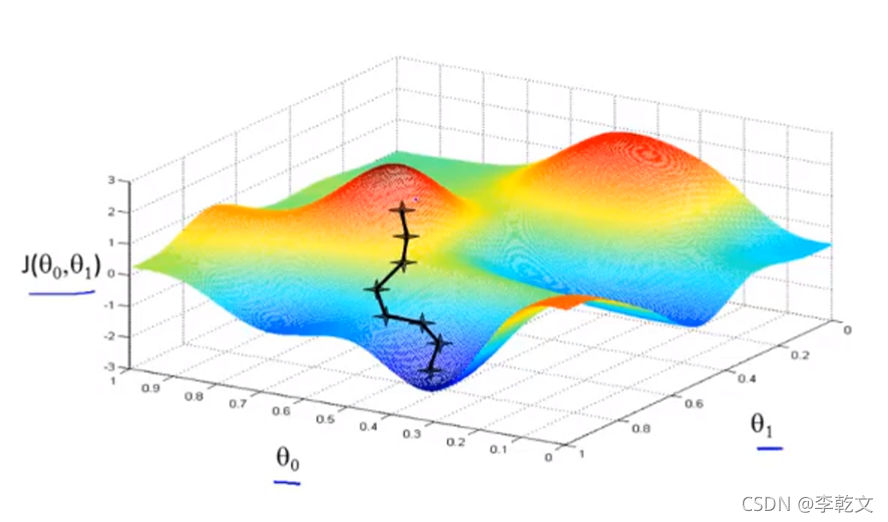
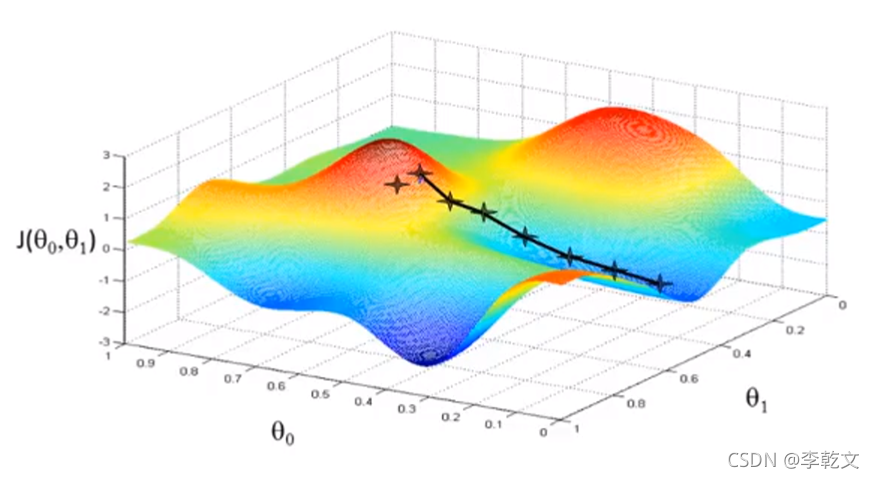
如果初始位置是另一个点，还有可能来到局部最低点，如下图所示：

三、算法实现

对$J(w_0,w_1)$中的$w_0,w_1$分别求偏导，求导相关知识可参考《导数与偏导》。
重复以下计算：
$w_0=w_0-\eta \ast \frac{\partial }{\partial w_0}J(w_0,w_1)=w_0-\eta \ast \frac{\partial }{\partial w_0}\frac{1}{2m}{\sum }_{i=1}^m[w_0+w_1{x}^{(i)}-y^{(i)}{]}^2=w_0-\eta \ast \frac{1}{m}{\sum }_{i=1}^m(w_0+w_1{x}^{(i)}-y^{(i)})$

$w_1=w_1-\eta \ast \frac{\partial }{\partial w_1}J(w_0,w_1)=w_1-\eta \ast \frac{\partial }{\partial w_1}\frac{1}{2m}{\sum }_{i=1}^m[w_0+w_1{x}^{(i)}-y^{(i)}{]}^2=w_1-\eta \ast \frac{1}{m}{\sum }_{i=1}^m(w_0+w_1{x}^{(i)}-y^{(i)})x^{(i)}$

$\eta$称之为学习率，控制梯度下降时每一段走的距离。
一直迭代计算，直到$w_0,w_1$变化很小为止，代表已经达到最小值或者局部最小值了，此时$w_0,w_1$确定下来。

上文中的$h(x)=w_0+w_{1}x$也可确定，输入房子面积，即可输出预测房价。

四、参考资料

• Machine Learning-Gradient descent ——Andrew Ng

• 梯度下降算法原理讲解

• 梯度向量与梯度下降法

• Vector Calculus: Understanding the Gradient