梯度向量与梯度下降法

    最近非常热门的“深度学习”领域，用到了一种名为“梯度下降法”的算法。梯度下降法是机器学习中常用的一种方法，它主要用于快速找到“最小误差”（the minimum error）。要掌握“梯度下降法”，就需要先搞清楚什么是“梯度”，本文将从这些基本概念：方向导数（directional derivative）与偏导数、梯度（gradient）、梯度向量（gradient vector）等出发，带您领略“深度学习”中的“最小二乘法”、“梯度下降法”和“线性回归”。

• 偏导数（Partial derivate）
• 方向导数（Directional derivate）
• 梯度（Gradient）
• 线性回归（linear regression）
• 梯度下降（Gradient descent）

一、方向导数

1，偏导数
  先回顾一下一元导数和偏导数，一元导数表征的是：一元函数 $f(x)$ 与自变量 $x$ 在某点附近变化的比率（变化率），如下：

$$f'(x_0) = \frac{\mathrm{d}f(x)}{\mathrm{d}x} \mid_{x=x_0} = \lim_{\Delta x \to 0}\frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x}$$
  而二元函数的偏导数表征的是：函数 $F(x,y)$ 与自变量 $x$ （或 $y$） 在某点附近变化的比率（变化率），如下：

Fx(x0,y0)=∂F∂x∣x=x0,y=y0=limΔx→0F(x0+Δx,y0)−F(x0,y0)Δx F x ( x 0 , y 0 ) = ∂ F ∂ x ∣ x = x 0 , y = y 0 = lim Δ x → 0 F ( x 0 + Δ x , y 0 ) − F ( x 0 , y 0 ) Δ x

$$F_x(x_0, y_0) = \frac{\partial F}{\partial x} \mid_{x=x_0,y=y_0} = \lim_{\Delta x \to 0}\frac{F(x_0 + \Delta x, y_0) - F(x_0, y_0)}{\Delta x}$$
  以长方形的面积 $z = F(x,y)$ 为例，如下图：

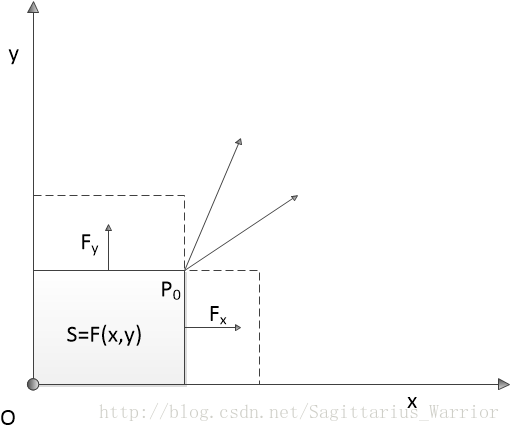
如果说 $z = F(x,y) = x \cdot y$ 表示以 P(x,y) 点和原点为对角点的矩形的面积，那么 $z = F(x,y)$ 在 $P_0$ 点对x 的偏导数表示 $P_0$ 点沿平行于 x 轴正向移动，矩形的面积变化量与 $P_0$ 点在 x方向的移动距离的比值

Fx(x0,y0)=∂F∂x=limΔx→0ΔSΔx F x ( x 0 , y 0 ) = ∂ F ∂ x = lim Δ x → 0 Δ S Δ x

$$F_x(x_0, y_0) = \frac{\partial F}{\partial x} = \lim_{\Delta x \to 0}\frac{\Delta S}{\Delta x}$$
同样地，可得
$$F_y(x_0, y_0) = \frac{\partial F}{\partial y} = \lim_{\Delta y \to 0}\frac{\Delta S}{\Delta y}$$
需要注意的是：
  矩形面积的这个例子有时候也很容易让人混淆，上图中无论 x 还是 y ，都是输入变量，输出变量 S 并没有用坐标轴的形式画出来。也就是说，这个例子实际上是一个三维空间的函数关系，而不是二维平面的函数关系。
  
向量角度看偏导数：
  偏导数向量 $\begin{bmatrix}F_x\\ F_y\end{bmatrix}$是坐标向量（原向量） [xy