Boosted Tree原理详解

简述

boosted Tree算法简要描述：

不断地添加树，不断地进行特征分裂来生长一棵树。每次添加一个树，其实是学习一个新函数，去拟合上次预测的残差。一个树在生长的过程中，挑选一个最佳特征的最佳分裂点，来进行特征分裂。

训练后会得到的模型是多棵树，每棵树有若干叶子节点，每个叶子节点对一个分数，假如来了一个样本，根据这个样本的特征，在每棵树上会落到对应一个叶子节点，总分数就是把落到的叶子节点的分数加起来，作为预测值。

理论推导

决策树

决策树的基础就不再赘述了。下面是一个推测一个人是否喜欢玩游戏的树的例子，结构如下：

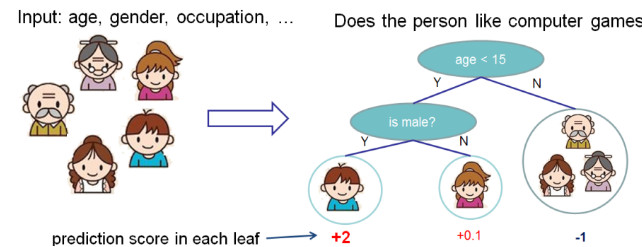
但一棵树的决策能力通常是不够强的，我们就使用多棵树预测值的和做最后的决策。

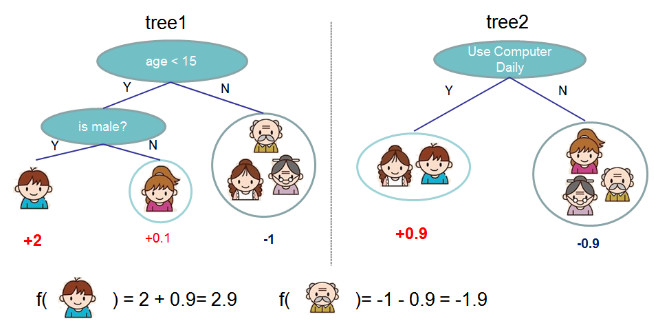
这就可以看出多个决策树 complement 的模型和目标函数了。

模型和目标函数

模型：
$$\widehat{y_i}=\sum _{k=1}^K{f}_k(x_i),f_k\in \mathcal{F}$$
其中 K 为 树的个数，$ \mathcal{F}$ 是 所有可能的 classification and regression trees (CART)集合。

目标函数：
$$Obj=\sum _{i=1}^{n}l(y_i,\widehat{y_i})+\sum _{k=1}^K\Omega (f_k)$$
其中，目标函数的第一项为训练损失，第二项为 树的复杂度（complexity of the Trees）

我们的模型是要学习 K 棵树，每次去拟合上一次的学习的残差。跟传统的有监督算法一样，目标函数有损失函数和正则项组成。与传统决策树不同的是，传统的决策树每次决策时 Heuristic （启发式） 的，比如 信息增益；而对于 boosted tree，每次决策都是 Objective 目标性质的，即与目标函数有关。

Additive Training

首先，我们要知道树的参数是什么？ 我们可以发现需要学习函数 $f_k$ ，它包含一棵树的结构和叶子的分数。学习树的结构是很复杂的，不像那些简单的优化问题可以很容易地得到梯度。一次性求解所有树是不可能的。因此我们使用“增加”策略：从一个预测常数开始，每次增加一个新函数。
$$\begin{gathered} {\widehat{y_i}}^{(0)}=0 \\ {\widehat{y_i}}^{(1)}=f_1(x_i)={\widehat{y_i}}^{(0)}+f_1(x_i) \\ {\widehat{y_i}}^{(2)}=f_1(x_i)+f_2(x_i)={\widehat{y_i}}^{(1)}+f_2(x_i) \\ ... \\ {\widehat{y_i}}^{(t)}=\sum _{k=1}^t{f}_k(x_i)={\widehat{y_i}}^{(t-1)}+f_t(x_i) \end{gathered}$$
可以看到，每一轮新的预测，都是上一次的预测值 + 本次学习的函数。

把最新的一次预测拆分为 上次预测值 + 本次学习的函数，即$\hat{y_i} ^{(t)} = \hat{y_i} ^{(t-1)} + f_t (x_i) $ ，则目标函数为：
$$\begin{gathered} Obj=\sum _{i=1}^{n}l(y_i,\widehat{y_i})+\sum _{k=1}^K\Omega (f_k) \\ =\sum _{i=1}^{n}l[y_i,{\widehat{y_i}}^{(t-1)}+f_t(x_i)]+\Omega (f_t)+constant \end{gathered}$$
目标函数中，目标值和上次预测值都是已知的，那么唯一要求的是新的函数 $f_t$ ，使目标函数最小，即${\sum }_{i=1}^{n}l[y_i,{\widehat{y_i}}^{(t-1)}+f_t(x_i)]+\Omega (f_t)$ 最小。

如果我们使用均方误差（MSE）作为损失函数，那么目标函数可以写为：
KaTeX parse error: No such environment: split at position 8: \begin{̲s̲p̲l̲i̲t̲}̲\text{obj}^{(t)…
MSE作为损失函数是很友好的，它包含一次项（通常称为残差 residual）和二次项。我们通常对目标函数进行泰勒展开，取到二次项

根据泰勒展开对目标函数进行变形，并取前两项：
$${\text{obj}}^{(t)}=\sum _{i=1}^n[l(y_i,{\hat{y}}_i^{(t-1)})+g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t^2(x_i)]+\Omega (f_t)+\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{t}$$
其中
KaTeX parse error: No such environment: split at position 8: \begin{̲s̲p̲l̲i̲t̲}̲g_i &= \partial…
可以看到，现在的目标函数的已知部分是：

• 上次预测的损失函数对应函数值
• 上次预测的损失函数的一级偏导数对应函数值
• 上次预测的损失函数的二级偏导数对应函数值

去掉已知项，目标函数变为：
$$\sum _{i=1}^n[g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t^2(x_i)]+\Omega (f_t)$$

这一些值根据上次预测结果可以求出来，唯一未知的就是新函数。而我们这里，是用一个棵树表示一个函数，每个叶子节点的输出值就是函数值，可枚举的。我们的目标就是把这些叶子节点的输出值求出来，使得目标最优。

模型的正则项

到此，我们还有一个重要的工作，即加上正则项，即定义树的复杂度 $\Omega (f)$ ，为此，我们细化树的定义为：
f t ( x ) = w q ( x ) , w ∈ R T , q : R d → { 1 , 2 , ⋯   , T } . f_t(x) = w_{q(x)}, w \in R^T, q:R^d\rightarrow \{1,2,\cdots,T\} . ft​(x)=wq(x)​,w∈RT,q:Rd→{1,2,⋯,T}.
这里 $w$ 是叶子上的分数向量，$q$ 是将每个数据点分配给相应叶子的函数， $T$ 是叶子的总数。XGBoost中，第一正则项为：
$$\Omega (f)=\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{w}_j^2$$
有不止一种的正则项定义方式，但上述这种 work 很好。

模型完整体

KaTeX parse error: No such environment: split at position 8: \begin{̲s̲p̲l̲i̲t̲}̲\text{obj}^{(t)…

这里 I j = { i ∣ q ( x i ) = j } I_j = \{i | q(x_i) = j \} Ij​={i∣q(xi​)=j} 是分配给第j个叶子的数据点索引集 ，注意公式第二行，我们家欢乐求和索引，这是因为所有数据点在同一个叶子上的分数相同。再引入 $G_j={\sum }_{i\in I_j}{g}_i$ 和 $H_j={\sum }_{i\in I_j}{h}_i$ ，目标函数可写为：
$${\text{obj}}^{(t)}=\sum _{j=1}^T[G_j{w}_j+\frac{1}{2}(H_j+\lambda )w_j^2]+\gamma T$$
这个公式中，$w_j$ 是相互独立的，且目标函数的形式是二次的，对于一个给定的结构，最好的 $w_j$ 和 最小的损失为：
KaTeX parse error: No such environment: split at position 8: \begin{̲s̲p̲l̲i̲t̲}̲w_j^\ast &= -\f…
第二个公式用于评估树结构 $q(x)$ 的好坏。

这些听起来有点复杂，让我们通过一个例子看看如何计算得分。 基本上，对于给定的树结构，我们将统计数据$g_i$ 和 $h_i$ 推送到它们所属的叶子，将统计数据加在一起，并使用公式计算树的有效性。 这个分数就像决策树中的杂质度量，除了它还考虑了模型的复杂性。如下：

参考链接

https://xgboost.readthedocs.io/en/latest/tutorials/model.html