关于提升思想,核心内容是将若干个弱可学习分类器线性组合成为一个强可学习分类器。其中,Adaboost 属于一种前向学习的二分类学习方法,且基本分类器可以不基于树,可用的范围更广。至于Boost Tree, Gradient Boost Tree 和 XGBoost 中基本的分类器是树结构的,包括二叉分类树和二叉回归树。
1、Adaboost
2、Boost Tree
3、Gradient Boost Tree
4、XGBoost
Adaboost
假设目前有M个基本分类器,N个样本,则一共需要循环M轮,每一轮循环要遍历所有的样本。其实说白了就是每一个弱分类器对所有样本都进行一次分类,在这过程中更新每一个样本和每一个分类器的权重,最后将这些弱分类器线性组合。具体思路为:
1、初始化每个样本的权重为 
2、从 m = 1:M
利用第m个分类器对每一个样本进行分类,根据分类结果计算该分类器的误差率  =
= 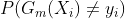
根据误差率计算该分类器的权重: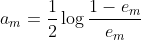
根据该分类器的权重更新每一个样本的权重: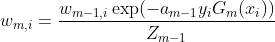
其中,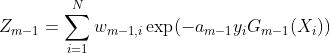 是一个规范化因子,用来保证所有样本的新权重在0到1之间。
是一个规范化因子,用来保证所有样本的新权重在0到1之间。
3、将训练完成的所有弱分类器线性组合成为一个强分类器:
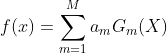
观察更新分类器和样本权重的方法,算法的出发点可以理解为:将容易分错的样本权重加大,也就是让这些样本成为衡量分类器性能的“试金石”,在此基础上,如果有哪些分类器可以将这些容易分错的样本分类正确的话,最终的错误率会相应地降低 ,从而分类器的权重会增加,也就是在最后M个分类器的结果中,我们更“看重”那些可以将容易分错的样本分对的分类器所得到的结果。
好,现在我们明白了Adaboost的算法思想,那么这样的思想是如何产生的呢?或者说这样的思想是否有据可查呢?其实,Adaboost是一种前向学习的二分类学习算法。而前向学习的思想是:将单个分类器逐一加入到最终的分类器中,也是一种 boosting 的思想。具体算法如下:
1、初始化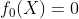
2、对于m = 1: M
(1)、得到损失函数,参数包括对当前分类器要赋予的权重和分类器中的参数:
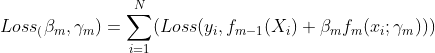
(2)、更新最终的分类器:
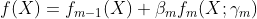
3、得到加法模型,也就是最终的分类器:
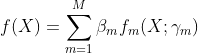
那么,Adaboost 和前向学习算法联系在哪里呢?不知道大家有没有好奇我们定义分类器权重的方法:
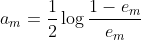
其实,在定义该权重的时候,我们已经使用了前向学习算法中计算分类器权重的思想:
在 Adaboost 中,假设我们已经得到了m-1个分类器的权重,也就是到了这一步:
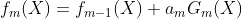
此时, 未知,但当前分类器的错误率
未知,但当前分类器的错误率 已知,当前损失函数为:
已知,当前损失函数为:
![Loss(a_m,G_m(X)) = \sum_{i = 1}^{N} \exp[-y_{i}(f_{m-1}(x_i) + a_m G_m(x_i)]](https://i-blog.csdnimg.cn/blog_migrate/566d9f2d1336e33aa1dcd7f3dcb9cc1d.gif)
一样是指数损失函数,将公式整理得到:
![Loss(a_m,G_m(X)) = \sum_{i = 1}^{N} \bar{w_{m,i}}\exp[-y_{i} a_m G_m(x_i)]](https://i-blog.csdnimg.cn/blog_migrate/05221debedf0bd93c23d053f66982a6e.gif)
其中,![\bar{w_{m,i}} = \exp[-y_i f_{m-1}(x_i)]](https://i-blog.csdnimg.cn/blog_migrate/9cda5d5a5c81722e553da34ed12fe24a.gif) ,该项在当前为常数,但当本次迭代结束而进入下一轮迭代时,会发生变化。
,该项在当前为常数,但当本次迭代结束而进入下一轮迭代时,会发生变化。
很容易看出,最小化损失函数与最小化以下函数是等价的:
![Loss(a_m,G_m(X)) = \sum_{i = 1}^{N} \bar{w_{m,i}}\exp[-y_{i} a_m G_m(x_i)]](https://i-blog.csdnimg.cn/blog_migrate/05221debedf0bd93c23d053f66982a6e.gif)
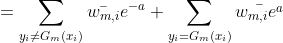
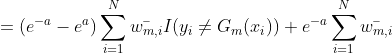
将该损失函数对 求导并使导数等于0,得到:
求导并使导数等于0,得到: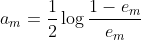 ,其中,
,其中,,证毕。
此时,模型更新成为了
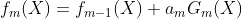
若进入下一轮迭代,即计算 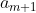 和
和 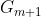 时,
时,![\bar{w_{m+1}} = \exp[-y_i f_m(x_i)]](https://i-blog.csdnimg.cn/blog_migrate/f29b784501454c16d2904a44ba7284ab.gif) ,又
,又 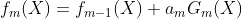 ,故:
,故:
![\bar{w_{m+1,i}} = \bar{w_{m,i}}\exp[-y_{i} a_m G_m{x_i}]](https://i-blog.csdnimg.cn/blog_migrate/e414f26548e2156615f29b98b6c40609.gif) ,也就是更新了下一轮迭代时每一个样本的权重,至此,本轮迭代结束。
,也就是更新了下一轮迭代时每一个样本的权重,至此,本轮迭代结束。
对于一个成熟的算法,我们可以得到它的泛化误差下界,Adaboost 也是一样。那么,它的误差范围是如何计算的呢?
根据指数损失的性质,不难得到:

而由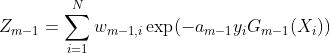 和
和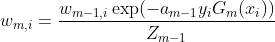 我们得到:
我们得到:
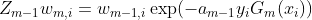 ,所以有:
,所以有:
 ,又因为:
,又因为: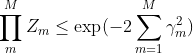 ,其中,
,其中,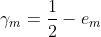 。故Adaboost算法是有误差下界的,而且该误差以指数速率下降。
。故Adaboost算法是有误差下界的,而且该误差以指数速率下降。
Boost Tree
前面所讲的 Adaboost 算法中,基函数可以是任何基础的分类器,但在 boost tree 算法中,是以决策树为基函数的。思想与前向学习一致,也是逐步地将单个树加入到最终的分类器中。boost tree的思想是这样的:假设目前已经加入了m-1颗树组成现有的分类器,那么对于每一个样本来说,当前的分类器对其都有一个预测值,那么这个预测值与样本真实的标签会产生一个残差。对于这个残差,我们可以理解为是当前分类器的“差强人意之处”,那么对于接下来要加入的新树来说,其使命就是消除掉这种“差强人意之处”,所以新加入的树对每个样本的预测值需要尽可能地拟合上述残差,这样一来,在加入后重新对样本进行预测的时候,得到的残差会更小。也就是说,在常见的分类问题中,基函数都是拟合训练集标签,而在以决策树为基函数的提升树算法中,是以拟合残差来作为目标。算法流程如下:
初始化,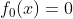
加入树,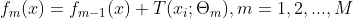
得到最终分类器:
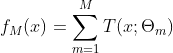
在计算新树时间,我们需要先计算当前分类器对每个样本的残差:
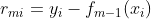
然后通过拟合残差得到需要加入的树。在寻找一颗新树的时候,我们需要对各个切分点所对应的残差进行衡量,最终选择残差最小的树加入到分类器中。
Gradient Boost
Gradient Boost 的思想与 Boost Tree 的思想一致,只是残差项由损失函数对当前模型的负梯度代替,这是因为当损失函数并非简单的平方损失和指数损失时,计算损失会很复杂。残差项表示如下:
![r_{m,i} = -[\frac{\partial L(y_i,f(x_i))}{\partial f(x_i)}]_{f(x) = f_{m-1}(x)}](https://i-blog.csdnimg.cn/blog_migrate/dfb63c99a264f362a0de174f799452d7.gif)
XGBoost
如果说boost tree 和 gradient boost 算法思想是在本次模型优化过程中,尽量拟合残差或者残差的代表项,那么 XGBoot 算法的思想就是在当前模型的优化过程中,最小化损失函数与自身有关的项。其中,与自身有关的项由损失函数的二阶泰勒展开得到,例如:
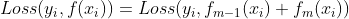
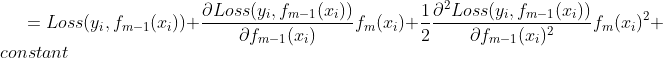
令
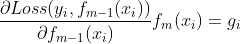 ,
,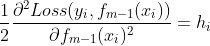 ,
,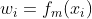 ,则有:
,则有:
其中,与当前模型有关的项为:
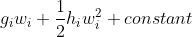 ,也就是说,我们需要最小化的项为:
,也就是说,我们需要最小化的项为:
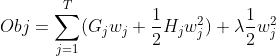 ,其中,T为叶子节点数,
,其中,T为叶子节点数,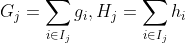 ,
,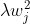 是对每个样本权重的一个限制项。
是对每个样本权重的一个限制项。
在此基础上,我们还需要加一个对模型复杂度的正则项,即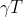 ,得到最终的目标函数:
,得到最终的目标函数:
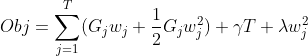 ,求该函数对
,求该函数对 的导数并令其等于0,我们得到:
的导数并令其等于0,我们得到: ,代入原式,有:
,代入原式,有:
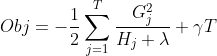 。至此,我们已经得到了衡量一颗新树性能的标准。那么,如何来划分叶子区间得到一颗新树呢?
。至此,我们已经得到了衡量一颗新树性能的标准。那么,如何来划分叶子区间得到一颗新树呢?
我们认为,只要分裂后比之前增益满足要求即可分裂:
![Gain = \frac{1}{2}[\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}]-\gamma](https://i-blog.csdnimg.cn/blog_migrate/88e054966181d9b3ee5182922c8f703e.gif) 。因为该算法是基于树的,所以在分裂节点的时候还涉及到特征的排序,故该算法也可以用作特征选择。
。因为该算法是基于树的,所以在分裂节点的时候还涉及到特征的排序,故该算法也可以用作特征选择。
总的来说,提升算法的思想就是多个弱分类器结果的线性相加为一个强分类器。其中,除Adaboost算法可以针对各种类型的分类器作为基本分类器外,其余的算法都是以决策树为基函数,因为都涉及到树的分裂。boost tree 和 gradient boost 算法在优化时,目标函数为对于所有样本,新模型的预测值与需要拟合的残差值的总和;而 XGBoost 的目标函数为对于每一个样本,定义的损失函数中与新模型的预测值有关的项的总和。其实说白了,就是优化时的目标函数定义不同。








 本文深入解析Adaboost、BoostTree、GradientBoostTree及XGBoost四大提升算法,阐述其核心思想与实现细节,强调线性组合弱分类器生成强分类器的原理。
本文深入解析Adaboost、BoostTree、GradientBoostTree及XGBoost四大提升算法,阐述其核心思想与实现细节,强调线性组合弱分类器生成强分类器的原理。
















 4182
4182

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








