【灵茶山艾府题单】基础算法精讲 高频面试题（9~16 二叉树 回溯）

灵茶山艾府 - 基础算法精讲 高频面试题
上一篇： 【灵茶山艾府题单】基础算法精讲 高频面试题（1~8 数组 链表）

09 二叉树

• 不要一上来就陷入细节，而是思考整棵树与左右子树的关系
  如104题，观察后可以发现整棵树的最大深度 = max(左子树的最大深度，右子树的最大深度) + 1，此时我们可以把原问题（计算整棵树的最大深度）分解成子问题（计算左/右子树的最大深度）的组合，且子问题与原问题是相似的，这意味着可以使用同样的代码处理它们。
• 当相似的问题之间具有嵌套关系，上一级问题需要子问题的计算结果，适合使用递归
  循环也是在用同一份代码处理相似问题。但是当相似的问题之间具有嵌套关系，上一级问题需要子问题的计算结果，更适合使用递归。
• 由于子问题的规模比原问题小，最小的子问题的的特征就是递归的边界条件
• 递：从原问题到达最小的子问题的过程；归：从最小的子问题开始，一路返回答案，直到原问题
• 计算机是靠栈保存结点，以此确定子问题的值应该返回给哪个结点的，因此空间复杂度O(n)
  演示网站：https://pythontutor.com/

104.二叉树的最大深度

题目 题解
整棵树的最大深度 = max(左子树的最大深度，右子树的最大深度) + 1
【方法一：在归的过程中计算结果】

class Solution {
public:
    int maxDepth(TreeNode *root) {
        if (root == nullptr) return 0;
        int l_depth = maxDepth(root->left);
        int r_depth = maxDepth(root->right);
        return max(l_depth, r_depth) + 1;
    }
};

【方法二：在递的过程中计算结果，配合全局变量】

class Solution {
public:
    int ans = 0;
    void dfs(TreeNode* root, int now_depth) {
        if(root == nullptr) return;
        now_depth++;
        ans = max(ans,now_depth);
        dfs(root->left,now_depth);
        dfs(root->right,now_depth);
    }
    int maxDepth(TreeNode* root) {
        dfs(root,0);
        return ans;
    }
};

10 二叉树

100.相同的树

题目 题解
两棵树是否相同 = 当前结点值是否相等 && 两棵左子树是否相同 && 两棵右子树是否相同
边界条件：两棵树都为空，返回true；一棵空一棵不空，返回false；
灵神此处边界条件的写法是相当天才的：if(!p || !q) return p == q;

101.对称二叉树

题目 题解
把树从中间分成两棵二叉树。与上一题相比，只是把比较对象换成了（左子树的左子结点，右子树的右子结点）和（左子树的右子结点，右子树的左子结点）。
边界条件：两棵树都为空，返回true；一棵空一棵不空，返回false；

110.平衡二叉树

题目 题解
一种普通的想法是仿照前面几题，整棵二叉树平衡 = 当前结点左右子树深度差不大于1 && 左子树平衡 && 右子树平衡。但是计算树的深度同样需要递归，这就导致递归套递归，造成了重复的计算。我们可以把判断是否平衡的过程融入到计算深度中。如果树是平衡的，我们就正常计算它的深度，如果不平衡，它的深度就记为-1；最后，只需要判断根结点的深度是不是-1，就能知道整棵树是否平衡了。

199.二叉树的右视图

题目 题解
灵神真的天才想法：先遍历右子树，再遍历左子树。同时，在遍历时记录当前结点的深度，如果这个深度是首次遇到，就说明当前结点在右视图可见，在代表答案的全局变量ans中添加该值。而这个深度是不是首次遇到，可以通过判断当前结点的深度和当前ans的长度是否一致来得到。
更通用的，也可以层序遍历二叉树，记录同一深度的最后一个结点。

11 二叉搜索树

有效的二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

98.验证二叉搜索树

ps. 在写递归的时候我经常遇到一个问题，就是想不清楚变量应该作为参数传入递归，还是作为一个全局变量写在外部。现在我总结出了一点经验：如果变量只在“递”的过程中更新，就要作为参数传入；如果变量在“归”的过程中更新，就要写成全局变量，或者作为函数返回值携带。

【方法一：前序遍历 - 由父及子更新边界】

要注意，对二叉搜索树的定义是子树的所有结点的值均大于/小于根结点的值，因此一个结点要知道它路径上之前所有结点的信息，才能确定边界。为每个结点传入它的边界，该边界由之前路径上的结点值更新得到。如果结点值在边界外，说明不是二叉搜索树。
在这个方法中，每个结点的边界在递的过程中确定，所以作为参数传入。

【方法二：中序遍历 - 判断结点值是否递增】
利用二叉搜索树的性质：中序遍历二叉搜索树，结点值为严格的递增序列。
这就产生了一个新问题，怎么记录结点值？一种想法是用一个全局数组记录中序遍历时访问过的结点值，然后递归结束后看数组是否递增……然而这会产生额外的空间和时间。实际上，我们可以在外部用一个变量记录上一个结点的值，只要比较当前结点的值是否大于上一个结点的值就可以了。如果<=上一个结点的值，就直接return false，否则就把变量更新为当前结点的值，作为下一个结点的比较对象。
在这个方法中，根结点的上一个结点是它的左子结点，上一个结点的值只能在递归左子结点返回时得到，所以写成全局变量。

【方法三：后序遍历 - 由子及父更新边界】

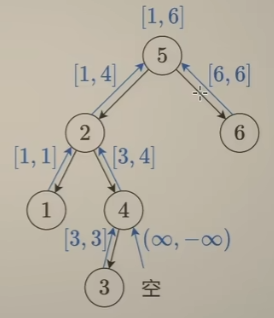
个人认为这个方法思路难想+实现方法复杂+细节很多，实用意义不大，可以作为练习了解下思路。
对于二叉搜索树中的结点来说，它的值应该大于左子树的最大值、小于右子树的最小值。所以我们可以由子及父的构建一个边界，分别记录目前遇到的最大值和最小值。为了将空结点纳入考虑范围，我们可以定义空结点的边界为（LLONG_MAX, LLONG_MIN）。
在这个方法中，边界显然是在递的过程中确定的，因此作为返回值携带。之所以没有用全局变量来写，大概是因为需要知道边界来自于左子树还是右子树，才能够正确地更新边界，因此作为返回值写更加直观。但是修改返回值也引入了新的问题，比如如何表示空结点、如何表示false等，需要仔细考虑。

12 二叉树

236.二叉树的最近公共祖先

题目 题解
公共祖先类的题真的好难想……感觉只能先半理解半背诵了。递归函数对二叉树进行了遍历，在归的过程中用返回值是否为空标记返回路径上是否包含p或q，若非空，其值可能为p结点、q结点或最近公共祖先结点（LCA)。在递的过程中，如果当前结点是空/p/q，就终止递归，并返回当前结点。这是因为，对于空结点，说明该路径递归到头还没有找到p或q，应该返回空；对于p或q结点，不管另一个结点在哪里，二者的公共祖先都不会在当前结点的子结点中，所以也应该终止该路径上的递归。

class Solution {
public:
    TreeNode *lowestCommonAncestor(TreeNode *root, TreeNode *p, TreeNode *q) {
        if (root == nullptr || root == p || root == q) {
            return root;
        }
        TreeNode *left = lowestCommonAncestor(root->left, p, q);
        TreeNode *right = lowestCommonAncestor(root->right, p, q);
        if (left && right) {
            return root;
        }
        return left ? left : right;
    }
};

235.二叉搜索树的最近公共祖先

题目 题解
这题比上一题好理解，因为可以借助二叉搜索树的性质判断p和q在当前结点的哪一边。
当前结点无需判断是否空的原因是，题目保证了有解，而我们每次只挑选同时包括p、q的一侧子树递归，递归到公共祖先就返回，因此不会遇到空结点。

13 二叉树

使用队列保存二叉树结点，每次处理队首结点，并把其子结点放入队尾。此时处理完了一层二叉树结点后，队列中为下一层全部的结点。常见结构为while(!q.empty){ for(int i=0;i<q.size();i++){ } }。

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        if(!root) return {};
        vector<vector<int>> ans;
        queue<TreeNode*> q;
        q.push(root);
        while(!q.empty()){
            vector<int> level;//每一层的遍历结果
            int n = q.size(); //每一层的结点数
            for(int i=0;i<n;i++){
                TreeNode* node = q.front();
                q.pop();
                level.push_back(node->val);
                if(node->left) q.push(node->left);
                if(node->right) q.push(node->right);
            }
            ans.push_back(level);
        }
        return ans;
    }
};

102.二叉树的层序遍历

题目 题解
使用队列保存二叉树结点，每次处理队首结点，并把其子结点放入队尾。此时处理完了一层二叉树结点后，队列中为下一层全部的结点。

103.二叉树的锯齿形层序遍历

题目 题解
与上一题基本一样。要实现每隔一层反转遍历方向，我们再需要反转的层可以：1.仍旧从左至右遍历，把遍历结果反转：if(ans.size()%2 == 1)，则把该层遍历结果反转后再添加。2.将队列改为双端队列deque，在上一层将子结点从队列头部插入，那么在下一层从头部pop时就是从右至左遍历了。

513.找树左下角的值

题目 题解
模板做法：每层从左到右遍历，记录每层第一个结点值，遍历结束后即为最后一行最左侧元素。
灵神做法：每层从右往左遍历，最后一个结点即为所求。

14 回溯 子集型

做题前请先看代码随想录：回溯算法理论基础
回溯部分的题目和题解虽然还是按照灵神的题单整理，但是我自己写的时候其实是参考代码随想录写的，所以有些思路与代码随想录更一致。代码随想录的回溯代码写得比较符合模板，比较适合新手学习。

vector<vector<int>> ans;//总的结果
vector<int> path;//每条路径的结果
void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}
vector<vector<int>> main_f() {
	backtracking(参数);
	return ans;
}

17.电话号码的字母组合

题目 题解
这题并不是子集型回溯，而是组合型回溯，放在这里大概是为了引出回溯的解题方法。如图所示，回溯的过程实际上是对树的深度优先遍历，每一条路径对应着一个可行的组合，我们只需要在路径结束时收集结果即可。组合型回溯的特点就是只需要收集叶子结点的结果。树的深度对应集合的数量，也就是digits的长度，每个结点的子结点数对应于下一个集合的长度。

78.子集

题目 题解
子集型回溯，在每个结点处收集答案。且为了避免重复（如取了元素1之后，子结点就只能从2、3中取），子结点应该从当前数字之后的数字中取，因此需要使用标记符startIndex标记位置

除了这种标准的回溯模板外，灵神还给出了一种站在输出角度的解题思路。子集的本质就是对于集合中的每个数，有取或不取两种操作。那么我们可以对每个数根据取或不取分类，构造一棵二叉树。最终，在叶子结点处收集答案即可。

131.分割回文子串

题目 题解

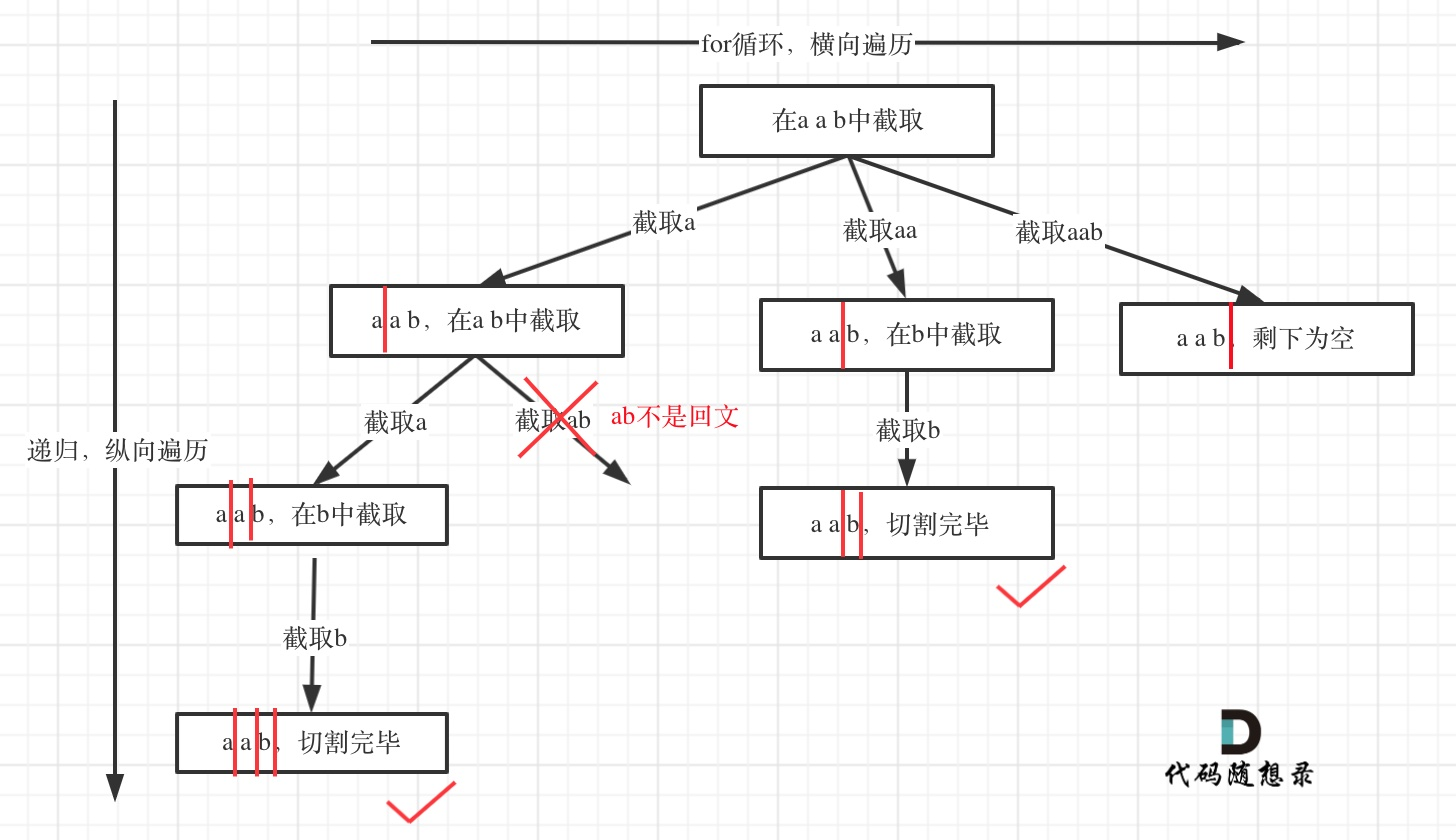
切割问题类似于组合问题，用startIndex标记最后一个切割线的位置，进行回溯。当切割线移动到字符串末尾，说明路径终止。在for循环横向遍历时，只对判断为是回文子串的子结点进行递归。

15 回溯 组合型

对于组合型回溯，我们通常可以进行一些剪枝处理，来提高效率。

77.组合

题目 题解

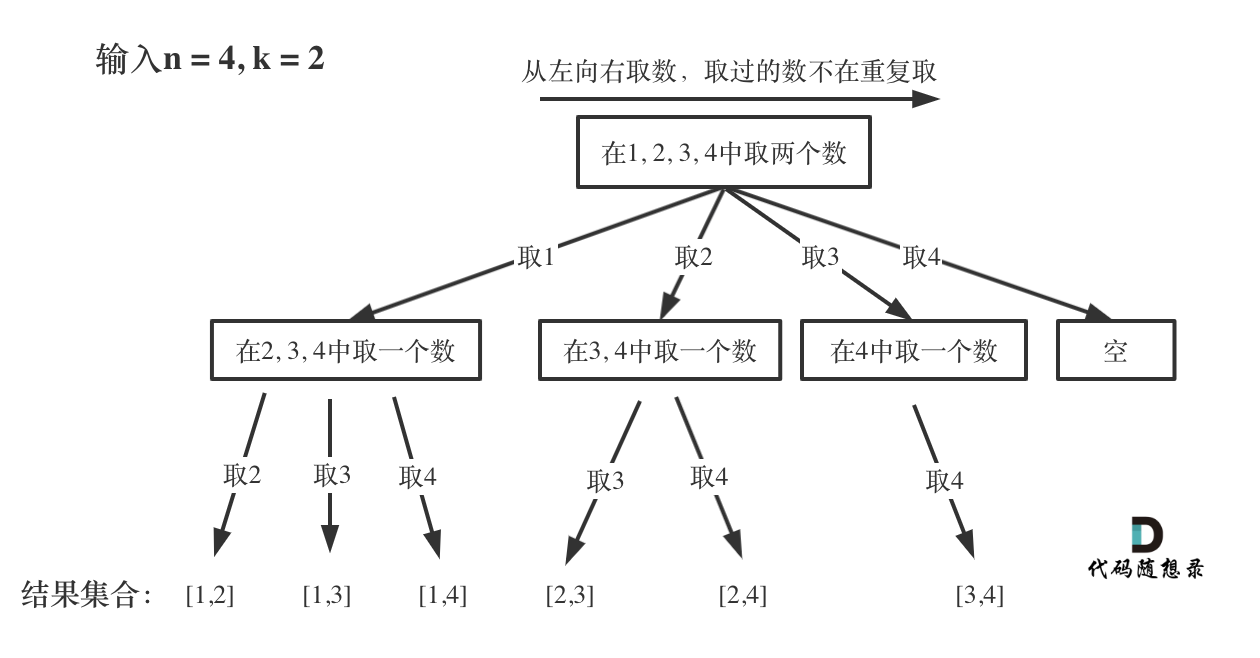
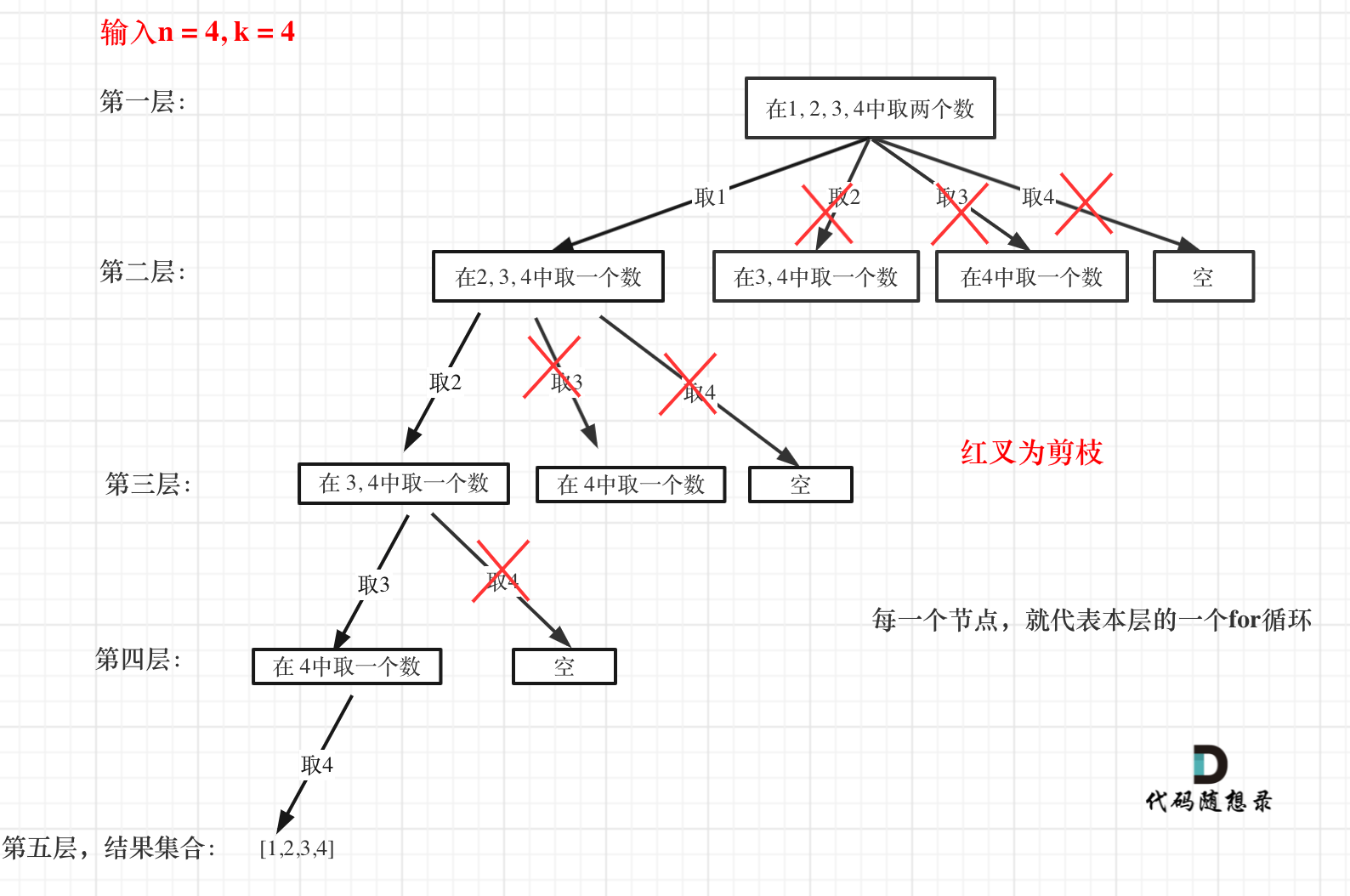
对于组合型回溯，我们可以进行剪枝。比如下图，对于n=4，k=4这种情况，我们在第一次取2的时候就可以终止该路径的递归，因为2之后只有3和4，我们最多只能取（2，3，4），不可能到4个数。所以，可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了，那么就没有必要搜索了。
列表中剩余元素（n-i） >= 所需需要的元素个数（k - path.size() 即 i <= n - (k - path.size()) + 1

216.组合总和III

题目 题解

两处剪枝：当前和已经大于目标和，剪枝；for循环中当前位置后的元素个数不足需要的元素个数，剪枝

22.括号生成

题目 题解
使用全局变量ans数组记录总结果，cur字符串记录每一个可能的组合
辅助函数void backtrack(int l,int r,int n); //已使用的左括号数l，已使用的右括号数r，括号总对数n
剪枝条件：l<r || l>n
存放结果条件：cur.size() == 2*n
每个结点有两个叶子结点，分别为增加左括号和增加右括号。

16 回溯 排列型

排列是有序的，也就是说 [1,2] 和 [2,1] 是两个集合，这和之前分析的子集以及组合所不同的地方。
对于排列问题，往往每层都是从0开始搜索而不是startIndex，并且需要used数组记录path里都放了哪些元素。

46.全排列

题目 题解

51.N皇后

题目 题解