斯特林公式(Stirling's approximation)取对数

最新推荐文章于 2020-02-21 15:03:43 发布

LostSpeed

最新推荐文章于 2020-02-21 15:03:43 发布

阅读量5.5k

点赞数

本文介绍斯特林公式及其在估算n!近似值的应用，并通过C++实现了一个实用的经验公式，用于估算n!结果所需的十进制字符数。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

斯特林公式用途

斯特林公式(Stirling's approximation) 用来求n!的近似值.

对斯特林公式取对数，可以估算结果位数.

e.g. pow(10, 2) = 100, log10(100) = 2

说明只需要(2+1)个字符就可以装下pow(10,2)的结果.

e.g. 用计算器算一下, fact(10) = 3628800, log10(3628800.0f); ///< 6.5597630328767940

说明只需要(6+1)个字符就可以装下fact(10)的结果.

斯特林公式资料

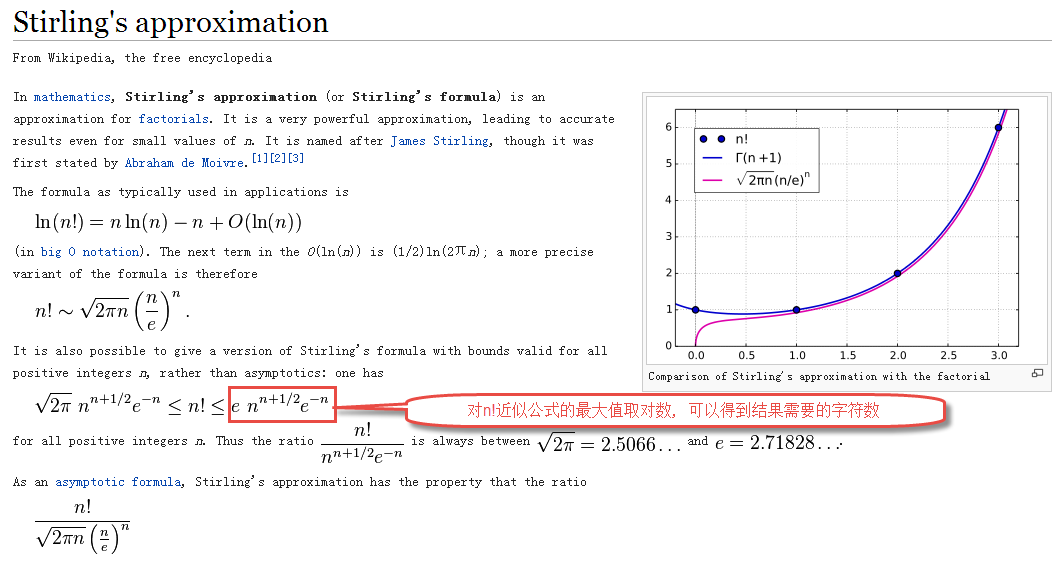
https://en.wikipedia.org/wiki/Stirling%27s_approximation

斯特林公式取对数的c++表达式推导

* 要推导的斯特林公式最大值公式

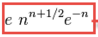
* 将上述公式写成c++表达式

#define E 2.71828

E * pow(n, (n+1)/2) * pow(E, -n);

* 对上述表达式取对数(log10), 可以得到用10进制字符表示n!需要几个字符

log10(E * pow(n, (n+1)/2) * pow(E, -n));

* 根据下面的对数公式将c++表达式化简

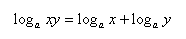
log10(E * pow(n, (n+1)/2) * pow(E, -n));

log10(E) + log10(pow(n, (n+1)/2)) + log10(pow(E, -n));

* 根据下面的对数公式将c++表达式化简

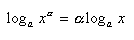
log10(E) + log10(pow(n, (n+1)/2)) + log10(pow(E, -n));

log10(E) + ((n+1)/2) * log10(n) - n * log10(E);

(1 - n) * log10(E) + ((n+1)/2) * log10(n) ;

((n+1)/2) * log10(n) + (1 - n) * log10(E) ;

表达式推导完成

log(n!) = ((n+1)/2) * log10(n) + (1 - n) * log10(E) ;

用于估算n!占用10进制字符位数的公式

估算的字符数要再加上1

log(n!) + 1= ((n+1)/2) * log10(n) + (1 - n) * log10(E) + 1;

估算n!结果字符串占用的10进制字符数 = ((n+1)/2) * log10(n) + (1 - n) * log10(E) + 1;

经验公式

用 ((n+1)/2) * log10(n) + (1 - n) * log10(E) + 1; 来估算n!占用的10进制字符个数，与实际情况相去甚远.

经过试验(用Windows计算器)，得出以下的经验公式, 基本符合n!结果所占用的10进制字符个数^_^

n * (log10(n) - log10(E)) + 4;

测试程序

/// @file \src_StirlingFormulaDerivation\main.c
/// @brief 估算大数n!需要字节数时, 搞一个简单好记的公式

#include <stdlib.h>
#include <stdio.h>
#include <math.h>

size_t fnLog10FactN(double n) {
    const double E = 2.71828;
    double dblCharCnt = 0;

    if (n <= 0)
        n = 1;

    /// 斯特林公式取对数
    // dblRc = ((n+1)/2) * log10(n)  + (1 - n) * log10(E) + 1;

    /// 由于斯特林公式取对数和用计算器算出的字符占用数相去甚远
    /// 修正一下公式, 基本符合实际情况
    dblCharCnt = n * (log10(n) - log10(E)) + 4;

    return (size_t)dblCharCnt;
}

void fnTestLogFactN() {
    size_t nIndex = 0;
    size_t nCharCnt = 0;

    /// Windows计算器能算出的最大阶乘为 fact(3248)
    for (nIndex = 0; nIndex <= 3248;) {
        nCharCnt = fnLog10FactN((double)nIndex);
        printf("Fact(%u)'s dblCharCnt = %u\n", nIndex, nCharCnt);

        if ((nIndex >= 0) && (nIndex < 10))
            nIndex ++;
        else if ((nIndex >= 10) && (nIndex < 100))
            nIndex += 10;
        else if ((nIndex >= 100) && (nIndex < 3200))
            nIndex += 100;
        else if ((nIndex >= 3200) && (nIndex < 3240))
            nIndex += 10;
        else
            nIndex ++;
    }
}

int main() {
    fnTestLogFactN();

    /** run result
    Fact(0)'s dblCharCnt = 3
    Fact(1)'s dblCharCnt = 3
    Fact(2)'s dblCharCnt = 3
    Fact(3)'s dblCharCnt = 4
    Fact(4)'s dblCharCnt = 4
    Fact(5)'s dblCharCnt = 5
    Fact(6)'s dblCharCnt = 6
    Fact(7)'s dblCharCnt = 6
    Fact(8)'s dblCharCnt = 7
    Fact(9)'s dblCharCnt = 8
    Fact(10)'s dblCharCnt = 9
    Fact(20)'s dblCharCnt = 21
    Fact(30)'s dblCharCnt = 35
    Fact(40)'s dblCharCnt = 50
    Fact(50)'s dblCharCnt = 67
    Fact(60)'s dblCharCnt = 84
    Fact(70)'s dblCharCnt = 102
    Fact(80)'s dblCharCnt = 121
    Fact(90)'s dblCharCnt = 140
    Fact(100)'s dblCharCnt = 160
    Fact(200)'s dblCharCnt = 377
    Fact(300)'s dblCharCnt = 616
    Fact(400)'s dblCharCnt = 871
    Fact(500)'s dblCharCnt = 1136
    Fact(600)'s dblCharCnt = 1410
    Fact(700)'s dblCharCnt = 1691
    Fact(800)'s dblCharCnt = 1979
    Fact(900)'s dblCharCnt = 2271
    Fact(1000)'s dblCharCnt = 2569
    Fact(1100)'s dblCharCnt = 2871
    Fact(1200)'s dblCharCnt = 3177
    Fact(1300)'s dblCharCnt = 3487
    Fact(1400)'s dblCharCnt = 3800
    Fact(1500)'s dblCharCnt = 4116
    Fact(1600)'s dblCharCnt = 4435
    Fact(1700)'s dblCharCnt = 4757
    Fact(1800)'s dblCharCnt = 5081
    Fact(1900)'s dblCharCnt = 5408
    Fact(2000)'s dblCharCnt = 5737
    Fact(2100)'s dblCharCnt = 6068
    Fact(2200)'s dblCharCnt = 6401
    Fact(2300)'s dblCharCnt = 6737
    Fact(2400)'s dblCharCnt = 7074
    Fact(2500)'s dblCharCnt = 7413
    Fact(2600)'s dblCharCnt = 7753
    Fact(2700)'s dblCharCnt = 8096
    Fact(2800)'s dblCharCnt = 8440
    Fact(2900)'s dblCharCnt = 8785
    Fact(3000)'s dblCharCnt = 9132
    Fact(3100)'s dblCharCnt = 9480
    Fact(3200)'s dblCharCnt = 9830
    Fact(3210)'s dblCharCnt = 9865
    Fact(3220)'s dblCharCnt = 9900
    Fact(3230)'s dblCharCnt = 9935
    Fact(3240)'s dblCharCnt = 9971
    Fact(3241)'s dblCharCnt = 9974
    Fact(3242)'s dblCharCnt = 9978
    Fact(3243)'s dblCharCnt = 9981
    Fact(3244)'s dblCharCnt = 9985
    Fact(3245)'s dblCharCnt = 9988
    Fact(3246)'s dblCharCnt = 9992
    Fact(3247)'s dblCharCnt = 9995
    Fact(3248)'s dblCharCnt = 9999
    */

    return 0;
}