学习率对线性回归模型的影响（基于梯度下降法）

        在机器学习领域，线性回归是一种基础且广泛使用的预测模型，用于建立输入特征和连续输出变量之间的线性关系。而，学习率，是一关键参数，解析来我们探讨学习率对梯度下降法在线性回归模型中的影响。

线性回归与梯度下降法

这里对线性回归和梯度下降不做过多解释。

线性回归模型通常采用以下形式：

梯度下降法通过迭代地调整模型参数来最小化代价函数，即均方误差（MSE）： 

梯度下降算法的目标是通过最小化代价函数 ，J(θ) 来找到参数 J(θ) 的最佳值。梯度下降的更新规则如下：

对于线性回归模型，参数 J(θ) 的梯度更新公式可以具体表示为：

        梯度下降算法通过重复应用上述更新规则来逐步调整参数，直到找到一个使代价函数最小化的参数集合。

        我们可以发现，学习率，就控制着每次更新的步长，学习率越大，步长越大，反之也成立，

但是不同的学习率，对我们的影响也是不同的，接下来，我们看一看不同学习率对结果的影响。

不同学习率的影响

        我们的最终目的是找到梯度更新公式的收敛部分，当我们设置合适的学习率时，看到的图片如下：

        看到，在迭代次数到100左右是，函数已经收敛了，这是一个好的结果，但是当我们设值不好的学习率时，就会出现不好的结果

        例如，学习率设置的过大：

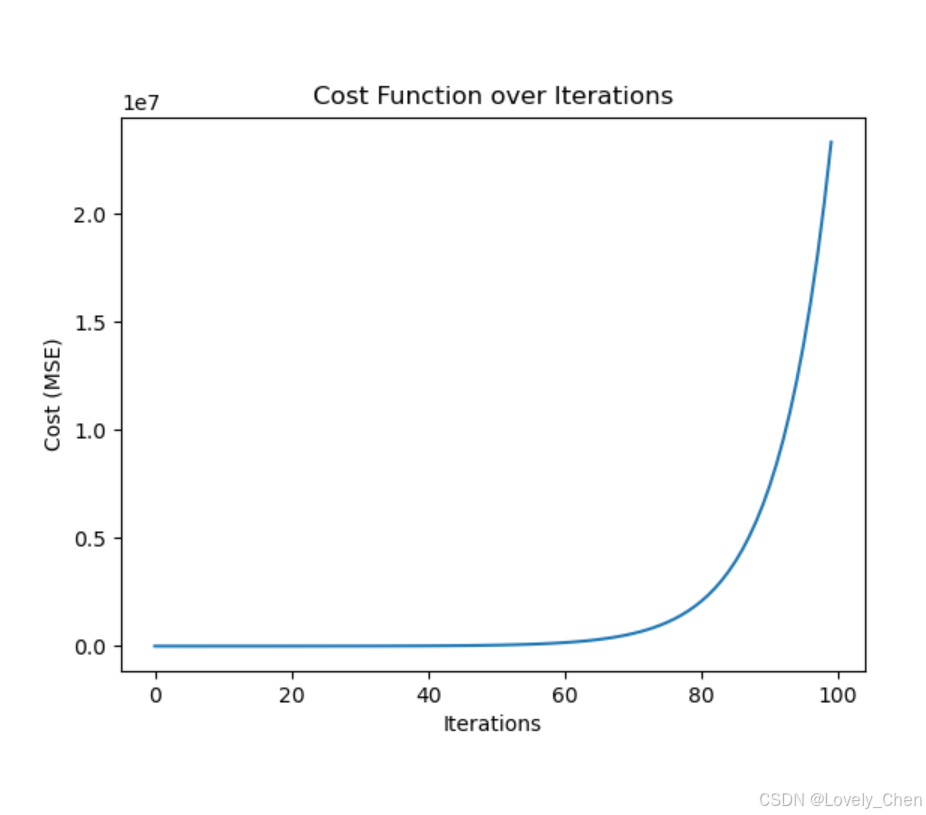
        很明显，这是一个错误的结果，但是为何回这样？那是因为，当我们设置的步长过大，反而会错过收敛点，这种情况下，只会越来越错。

        当然，也不是学习率越小越好，当我们设置的学习率过小的时候，它的步长就会很小，会迭代好多次才可以找到，其次，也会导致训练的成本和时间增长。

        所以设置一个合适的学习率，是一个重要的环节。

        最后放上我用python模拟的代码：

import numpy as np
import matplotlib.pyplot as plt

# 设置随机种子以获得可重复的结果
np.random.seed(0)

# 生成随机数据点
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)


# 定义线性模型
def predict(X, w, b):
    return np.dot(X, w) + b


# 定义均方误差代价函数
def compute_mse(y_pred, y_true):
    return ((y_pred - y_true) ** 2).mean()


# 梯度下降法
def gradient_descent(X, y, w, b, learning_rate, iterations):
    cost_history = []
    for i in range(iterations):
        y_pred = predict(X, w, b)
        cost = compute_mse(y_pred, y)
        cost_history.append(cost)

        # 计算梯度
        dw = (2 / len(X)) * np.dot(X.T, (y_pred - y))
        db = (2 / len(X)) * np.sum(y_pred - y)

        # 更新参数
        w -= learning_rate * dw
        b -= learning_rate * db

    return w, b, cost_history


# 初始化参数
w = np.random.randn()
b = np.random.randn()

# 梯度下降参数
learning_rate =0.001
iterations = 100

# 执行梯度下降
w, b, cost_history = gradient_descent(X, y, w, b, learning_rate, iterations)

# 绘制代价函数图像
plt.plot(cost_history)
plt.title('Cost Function over Iterations')
plt.xlabel('Iterations')
plt.ylabel('Cost (MSE)')
plt.show()