数据结构实验之最小生成树的2种算法实现【附流程图&代码】

一、实验目的

1）理解并熟练掌握最小生成树的两种算法实现（Kruskal算法【加边】 && prim算法【加点】）及其应用。
2）熟练掌握带权图的存储结构。
3）熟练掌握，学会运用“贪心”这一思想。

二、实验环境

1）自备计算机，windows操作系统以及相关的编译器（如Devc++）。

三、实验要求

1）完成带权图的存储和两种算法对应的最小生成树的生成。
2）灵活地把最小生成树应用于解决生活实际问题。

四、实验原理

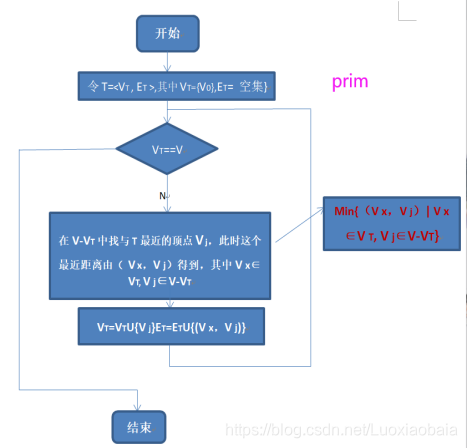
五、实验内容

代码如下：
1.用Kruskal算法实现：

#include <stdio.h>
#define VER_LEN (101)
#define EDGE_LEN (10001)
typedef struct {
    int u,v,cost;
}edge;

edge Edge[EDGE_LEN];
int Parent[VER_LEN];
int Size[VER_LEN];
int Flag[VER_LEN];

// 排序，按照边的权重，从小到大排序
void sort(int edge_num){
    int i,j;
    int temp_u, temp_v, temp_cost;

    for(i = 1; i < edge_num; i++) {
        for(j = 1; j <= edge_num - i; j++) {
            if(Edge[j].cost > Edge[j+1].cost) {
                temp_u = Edge[j].u;
                temp_v = Edge[j].v;
                temp_cost = Edge[j].cost;
                Edge[j].u = Edge[j+1].u;
                Edge[j].v = Edge[j+1].v;
                Edge[j].cost = Edge[j+1].cost;
                Edge[j+1].u = temp_u;
                Edge[j+1].v = temp_v;
                Edge[j+1].cost = temp_cost;
            }
        }
    }
}

void init(int ver_num) {
    int i;
    for(i=1; i<=ver_num; i++) {
        Parent[i]=i;// 将parent初始化为自身
        Size[i]=1;/*将size初始化为1，用于按秩压缩（
		如果不需要进行按秩压缩，不需要这个数组信息）*/
    }
}

int find(int vertex) {
    if(vertex != Parent[vertex]) {
        Parent[vertex]=find(Parent[vertex]);//路径压缩
    }
    return Parent[vertex];
}

int union_set(int i) {
    int parent_u = find(Edge[i].u);
    int parent_v = find(Edge[i].v);
    
    // 节点u和v已经在同一颗树上了
    if(parent_u == parent_v)     return 0;
    
    // 按秩压缩，将秩小一些的树加入到秩大一些的树
    if(Size[parent_u] > Size[parent_v]) {
        Parent[parent_v] = parent_u;
        Size[parent_u] += Size[parent_v];
    } else {
        Parent[parent_u] = parent_v;
        Size[parent_v] += Size[parent_u];
    }
    return 1;
}

void Kruskal(int ver_num, int edge_num) {
    int i,counter;

    // 排序，按照边的权重，从小到大排序
    sort(edge_num);

    // 进行初始化
    init(ver_num);

    counter = 0;
    // 按照边的权重，从小到大遍历所有的边
    // 直到编译完所有边，或者生成了最小生成树为止
    for(i = 1; i <= edge_num && counter < ver_num-1; i++) {
        // 当新加入的边会形成环时，需要舍弃
        if(union_set(i) == 0)    continue;
        
        // 将新加入的边的编号保存在Flag数组中，以便输入
        counter++;
        Flag[counter] = i;
    }
}

int main() {
    int i,ver_num, edge_num;
    printf("输入顶点数和边数：\n");
    scanf("%d %d", &ver_num, &edge_num);
    printf("输入图的信息：\n");
    for(i = 1; i <= edge_num; i++)
        scanf("%d %d %d", &Edge[i].u, &Edge[i].v, &Edge[i].cost);
        
    Kruskal(ver_num, edge_num);
    printf("Kruskal算法输出最小生成树：\n");
    for(i = 1; i < ver_num; i++)
        printf("%d to %d\n", Edge[Flag[i]].u, Edge[Flag[i]].v);
    return 0;
}

2.用prim算法实现：

#include <stdio.h>
#define MAXINT (0X7FFF7FFF)
#define VER_LEN (101)
typedef struct {
    int cost;
    int flag;
    int pre;
} vertex;

int Graph[VER_LEN][VER_LEN];
vertex Vertex[VER_LEN];

// 初始化图的数据，初始化为两点之间互不连接
void init_graph(int length) {
    int i, j;
    for(i = 1; i <= length; i++)
      for(j = 1; j <= length; j++)
        Graph[i][j] = MAXINT;
}

void prim(int start, int length) {
    int i,j;
    int min_cost, min_v;

    // 根据初始顶点start，初始为各顶点的相关信息
    // cost表示权重，flag表示是否已经加入最小生成树，pre表示其parent节点
    for(i = 1; i <= length; i++) {
        Vertex[i].cost = Graph[start][i];
        Vertex[i].flag = 0;
        Vertex[i].pre = start;
    }

    // 将初始顶点加入到最小生成树中
    Vertex[start].cost = 0;
    Vertex[start].flag = 1;

    for(i = 2; i <= length; i++) {
        min_cost = MAXINT;
        // 找出cost最小的边
        for(j = 1; j <= length; j++) {
            if(Vertex[j].flag == 0 && Vertex[j].cost < min_cost) {
                min_cost = Vertex[j].cost;
                min_v = j;
            }
        }

        // 将上面找出来的cost最小的边的顶点加入到最小生成树中
        Vertex[min_v].flag = 1;

        // 根据上面新加入到最小生成树的顶点调整各顶点的cost值
        for(j = 1; j <= length; j++) {
            if(Vertex[j].flag == 0 && Vertex[j].cost > Graph[min_v][j]) {
                Vertex[j].cost = Graph[min_v][j];
                Vertex[j].pre = min_v;
            }
        }
    }
}

int main() {
    int i;
    int ver_num, edge_num;
    int edge_u, edge_v, cost;

    printf("输入顶点数和边数：\n");
    scanf("%d %d", &ver_num, &edge_num);
    init_graph(ver_num);
    
    printf("输入图的信息：\n");
    for(i = 1; i <= edge_num; i++) {
        scanf("%d %d %d", &edge_u, &edge_v, &cost);
        Graph[edge_u][edge_v] = cost;
        Graph[edge_v][edge_u] = cost;
    }

    prim(1, ver_num);
    printf("prim算法输出最小生成树：\n");
    for(i = 2; i <= ver_num; i++)
        printf("%d to %d, the cost is %d\n", Vertex[i].pre, i, Vertex[i].cost);
    return 0;
}

六、运行结果

七、实验总结

通过这一实验，我更加深入地理解了“贪心”的思想，熟练掌握了最小生成树的两种算法（Kruskal【加边】和prim【加点】）和图的存储结构，并且能够用它们来解决生活中的一些实际问题。