地理哈希网格 Geohash Grid

Lyh1gguyg

于 2024-10-04 19:03:08 发布

阅读量240

点赞数 5

文章标签：哈希算法

本文链接：https://blog.csdn.net/Lyh1gguyg/article/details/142706157

版权

题目描述

“地理哈希”是一个将二维平面坐标编码为整数的过程，这将为数据库中地理数据的存储和查询带来方便。在这个问题中，一个地图是一个建立在标准二维笛卡尔坐标系上的2^n行2^n列的矩形网格，越往右x坐标越大，越往上y坐标越大。一个地图格子是一个单位正方形，满足其左下角的点的坐标为(x,y)，其中0<=x,y<2^n。

在2^n行2^n列的地图上一共有2^(2n)个格子。对于一个格子c，它的地理哈希值h(c)是一个2n位的非负二进制整数。从最高位开始考虑整个地图，然后重复下面两个步骤n次，即可得到c的地理哈希值h(c)：

1.把地图分成左右两个面积相等的区域，如果格子c在左半边，那么这一位是0，否则是1。然后将考虑范围缩小到c所在的那半边地图。

2.把地图分成上下两个面积相等的区域，如果格子c在下半边，那么这一位是0，否则是1。然后将考虑范围缩小到c所在的那半边地图。

一个“地理哈希区间”[a,b]表示所有哈希值在[a,b]之间的格子。通常应用中，我们会用一些地理哈希区间去近似表示地图。给定一个格子集合C，以及一个正整数t，那么C的最优t近似是指使用不超过t个地理哈希区间，覆盖住所有C中的格子（覆盖其它格子是允许的），同时满足覆盖住的区域的面积最小。

给定一个地图以及一个格子集合C，C用一个边平行于坐标轴的简单多边形来表示。然后给定q个询问t_1,t_2,...,t_q，对于每个询问t_k，你需要求出C的最优t_k近似覆盖住的区域的面积。

输入格式

第一行包含一个正整数n(1<=n<=30)，表示地图的尺寸的以2为底的对数。

第二行包含一个正整数m(4<=m<=200)，表示多边形顶点的个数。

接下来m行，每行两个整数x_i,y_i(0<=x_i,y_i<=2^n)，按逆时针依次表示多边形每个顶点的坐标。

输入数据保证多边形不自交，边平行于坐标轴，且不存在相邻两条边是平行的。

接下来一行包含一个正整数q(1<=q<=100000)，表示询问的个数。

接下来q行，每行一个正整数t_1,t_2,...,t_q(1<=t_i<=10^9)，依次表示每个询问。

输出格式

输出q行，每行一个正整数，依次回答每个询问。

输入输出样例

输入 #1复制

输出 #1复制

说明/提示

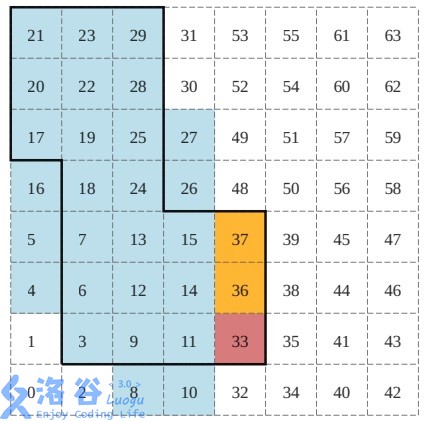
区间[3,29]、[33,33]和[36,37]组成最优3近似，其覆盖住的总面积为30。

题解

首先考虑暴力，判断每个格子是否在多边形内部，找到其编号最小和编号最大的格子，设其编号为 l,rl,r。

显然 l \sim rl∼r 中的格子不一定都是多边形内部，里面有一些间隔。

那么如果查询 11，则肯定返回 r-l+1r−l+1。

否则查询 kk，找到 l \sim rl∼r 中长度前 k-1k−1 大的间隔，设其长度和为 lenlen，那么答案为 r-l+1-lenr−l+1−len。

因为用 kk 个区间表示此多边形，最优策略就是将其前 k-1k−1 大的间隔去掉。

因此找到多边形在 [l,r][l,r] 中的所有间隔，按照长度排序，前缀和预处理即可。

所以接下来的问题是找到间隔长度以及个数。

题目中出现了 2^n2n，考虑用分治解决。

使用类似线段树的分治思想求出所有间隔。设分治到区间 [l,r][l,r]，分治的任务是找出 [l,r][l,r] 内部的间隔，返回 [l,r][l,r] 中最小/最大的内部格子。

虽然格子数量非常多，但多边形的顶点数量是比较少的。如果一个分治区间对应的矩形内有顶点，称为特殊区间。特殊区间的数量只有 O(nm)O(nm) 个，可以直接往下递归处理。

非特殊区间对应的矩形内没有顶点，有两种情况：

没有边经过矩形，判断其在多边形内部还是外部，直接返回。
有边经过矩形，要么全是竖线，要么全是横线。如果全是竖线的矩形分成上下两部分，那这两部分是完全相同的，只需要递归上半边，上半边找到的间隔都要乘以 22，可以在递归时传一个系数，遇到这种情况系数乘上 22。

判断一个格子在内部还是外部可以看从格子中心出发的射线和边的相交次数。

这样分治会有一堆区间不会访问，分析下复杂度。

非特殊区间一开始都是由特殊区间分裂产生的，这样的情况最多发生 O(nm)O(nm) 次。然后由特殊区间产生的非特殊区间继续递归，继续产生最多 O(nm)O(nm) 个非特殊区间，所以总状态 O(n^2m^2)O(n2m2) 个。每个区间在处理的时候枚举多边形的每条边，判断下内部是否有顶点，是否全是竖线/横线，以及如果为空，是在多边形内部还是外部。复杂度 O(n^2m^3)O(n2m3)。

另：这题将多边形的边也分治下去，可以把复杂度降至 O(n^2m^2)O(n2m2)。

大概吧。

感觉我的时间复杂度分析在胡扯。

代码：

#include<bits/stdc++.h>
using namespace std;
#define vi vector<int>
#define mp make_pair
#define ll long long
const int M=205,MAXM=1e6+5;
int n,m;
int ax[M],ay[M];// 多边形转折点

map<ll,int> Hash;// 空隙长度对应编号。
int tot;// 不同空隙数量。
ll val[MAXM],cnt[MAXM];// val: 空隙长度; cnt: 相同空隙数量。
int p[MAXM];// p: 排序用数组。
ll pre[MAXM],valpre[MAXM];// pre: 前缀的空隙数量; valpre: 前缀的空隙长度和。
bool cmp(int x,int y) {return val[x]>val[y];}

bool check(int x,int y) {// 查看 (x,y) 在是否多边形内部。
    int fg=0;            // 从 (x,y) 到 (0,y) 的射线，判断有几个交点。
    for(int i=1;i<=m;i++) {
        if(ay[i]==ay[i+1]) continue;
        if(ax[i]>x) continue;
        if((ay[i]<=y&&ay[i+1]>y)||(ay[i]>y&&ay[i+1]<=y)) fg^=1;
    }
    return fg;
}

int calc(int lx,int ly,int rx,int ry,const vi &e) {// 0: 区间内没有边. 1: 区间内全竖边. 2: 区间内全横边. 3: 区间内有点（横边竖边都有）。
    int fg=0;
    for(auto i:e) {
        if(ax[i]==ax[i+1]) { // 竖边
            if(ax[i]<=lx||ax[i]>rx) continue;

            if(ay[i]>ly&&ay[i]<=ry) fg=3;
            else if(ay[i+1]>ly&&ay[i+1]<=ry) fg=3;
            else if(ay[i]<=ly&&ay[i+1]<=ly) continue;
            else if(ay[i]>ry&&ay[i+1]>ry) continue;
            else fg|=1;
        }
        else {// 横边
            if(ay[i]<=ly||ay[i]>ry) continue;

            if(ax[i]>lx&&ax[i]<=rx) fg=3;
            else if(ax[i+1]>lx&&ax[i+1]<=rx) fg=3;
            else if(ax[i]<=lx&&ax[i+1]<=lx) continue;
            else if(ax[i]>rx&&ax[i+1]>rx) continue;
            else fg|=2;
        }
    }
    return fg;
}

void add(ll x,ll sz) {// 将每个空隙加入 Hash 表里。
    if(!x) return;
    if(Hash.count(x)==0) {
        tot++;Hash[x]=tot;
        val[tot]=x;
    }
    cnt[Hash[x]]+=sz;
    return;
}

pair<ll,ll> solve(ll l,ll r,int lx,int ly,int rx,int ry,int cut,int len,ll mul,const vi &e) {// l,r: 分治的左右端点; lx,ly,rx,ry: 左右端点的坐标值。
                                                                                  // cut: 0沿竖边向左右分治. 1沿横边向上下分治; len: 长边（竖边）的长度为 2^(len+1); mul: 携带的系数。
                                                                                  // 返回值: 多边形在区间内的最小 / 最大编号。
                                                                                  // e: 多边形的边。
    if(l>r) return mp(0,0);
    ll mid=(l+r)/2;
    int tg=calc(lx,ly,rx,ry,e);// 0: 区间内没有边. 1: 区间内全竖边. 2: 区间内全横边. 3: 区间内有点（横边竖边都有）。
    if(tg==0) {
        tg=check(lx,ly);// 0: 区间在多边形外面. 1: 区间在多边形内部。
        if(tg) return mp(l,r);
        return mp(-1,-1);
    }

    if((cut==0&&tg==2)||(cut==1&&tg==1)) {// 两边多边形相同，系数乘 2。
        pair<ll,ll> x;
        if(!cut) x=solve(l,mid,
                         lx,ly,rx-(1<<len),ry,
                         1,len,mul*2,e);

        else     x=solve(l,mid,
                         lx,ly,rx,ry-(1<<len),
                         0,len-1,mul*2,e);

        ll front=x.first,back=x.second;
        if(front==-1) return x;

        add(front+(mid-l+1)-back-1,mul);
        return mp(front,back+(mid-l+1));
    }

    vi e1,e2;e1.clear();e2.clear();
    pair<ll,ll> x,y;
    if(!cut) {
        for(auto i:e) {
            if(ax[i]==ax[i+1]) { // 竖边
                if(ax[i]<=rx-(1<<len)) e1.push_back(i);
                else e2.push_back(i);
            }
            else { // 横边
                int mn=min(ax[i],ax[i+1]),mx=max(ax[i],ax[i+1]);
                if(mn<=rx-(1<<len)) e1.push_back(i);
                if(mx>rx-(1<<len)) e2.push_back(i);
            }
        }

        x=solve(l,mid,
                lx,ly,rx-(1<<len),ry,
                1,len,mul,e1);

        y=solve(mid+1,r,
                lx+(1<<len),ly,rx,ry,
                1,len,mul,e2);
    }
    else {
        for(auto i:e) {
            if(ay[i]==ay[i+1]) { // 横边
                if(ay[i]<=ry-(1<<len)) e1.push_back(i);
                else e2.push_back(i);
            }
            else { // 竖边
                int mn=min(ay[i],ay[i+1]),mx=max(ay[i],ay[i+1]);
                if(mn<=ry-(1<<len)) e1.push_back(i);
                if(mx>ry-(1<<len)) e2.push_back(i);
            }
        }

        x=solve(l,mid,
                lx,ly,rx,ry-(1<<len),
                0,len-1,mul,e1);
        y=solve(mid+1,r,
                lx,ly+(1<<len),rx,ry,
                0,len-1,mul,e2);
    }

    ll front=x.second,back=y.first;
    ll k=back-front-1;
    if((front!=-1)&&(back!=-1)) add(k,mul);

    if(front==-1) return y;
    if(back==-1) return x;
    return mp(x.first,y.second);
}
int main() {
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++) scanf("%d%d",&ax[i],&ay[i]);
    ax[m+1]=ax[1],ay[m+1]=ay[1];

    vi Nora;Nora.clear();for(int i=1;i<=m;i++) Nora.push_back(i);
    pair<ll,ll> Koishi=solve(0,(1ll<<(n*2))-1,
                               0,0,(1<<n)-1,(1<<n)-1,
                               0,n-1,1,Nora);

    ll all=Koishi.second-Koishi.first+1;

    for(int i=1;i<=tot;i++) p[i]=i;
    sort(p+1,p+tot+1,cmp);
    for(int i=1;i<=tot;i++) {// 计算前缀和
        int x=p[i];
        pre[i]=pre[i-1]+cnt[x];
        valpre[i]=valpre[i-1]+1ll*cnt[x]*val[x];
    }

    int T;
    scanf("%d",&T);
    while(T--) {
        int x;scanf("%d",&x);x--;
        if(x>pre[tot]) {printf("%lld\n",all-valpre[tot]);continue;}

        int l=0,r=tot,mid,k=0;
        while(l<=r) {// 二分找到最小的 k 使得 x<=pre[k]。
            mid=(l+r)>>1;
            if(pre[mid]>=x) k=mid,r=mid-1;
            else l=mid+1;
        }

        ll num=0;// num: 前 x 大间隙长度和。
        if(k) num=valpre[k-1];
        num+=1ll*(x-pre[k-1])*val[p[k]];

        printf("%lld\n",all-num);
    }
    return 0;
}