对于部分全同态密码的总结

1.第二代全同态

1.1BGV

1.1.1算法构造

（1）.密钥生成

（2）.加密

这里的明文

（3）.解密

1.1.2同态运算

同态乘法

这里的reduce level是指判断噪声是否过大，若是，则进行ModulusSwitch操作，减小噪声

1.2BFV

1.2.1算法构造

（1）.密钥生成

（2）.加密

（3）.解密

1.2.2同态运算

同态乘法

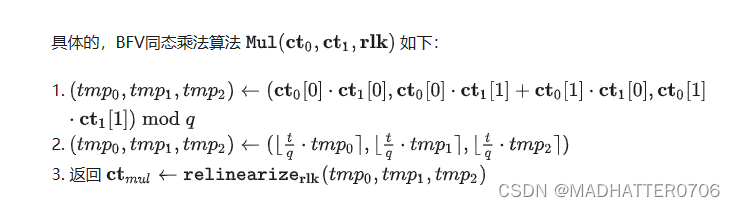
其中第二步进行Scale Invariant操作，即让密文乘上，在四舍五入求取整数，通过这种方式减小密文中原有的噪声，但同时也会产生新的噪声，详见下面的分析。

1.3 CKKS

1.3.1算法构造

（1）.密钥生成

（2）.加密

密文也可以写作如下格式

其中由于待加密的消息是复数，因此编码后所得到的多项式系数可能为浮点数，为了将其移至整环上，通过△实现，这里的△也体现了精度。

（3）.解密

1.3.2同态运算

同态乘法

这里的P实际上时Powerof操作，P^-1是指decompose操作，后面在说明

1.4二代同态密码算法的特点

1.4.1SIMD编码

编码的目的是为了将多条数据打包成一个明文，对明文的一次操作可以对应多条数据的分别操作。

第二代FHE，包括BGV，BFV，CKKS，目前在整体计算性能（不考虑bootstrapping自举操作）上是最优的。

其中一个关键性技术就是SIMD (Single Instruction Multiple Data)。通过SIMD, 可以将一个定义在上的向量编码成 上的一个多项式。换句话说，SIMD使得FHE可以直接操作一组向量。依据中国剩余定理的同构性质， 上多项式的加法和乘法等价于向量的对应元素加法（point-wise addition）和对应元素乘法（point-wise multiplication），因此，SIMD编码使得并行化同态加法和同态乘法成为可能。FHE的系统参数设定导致SIMD编码的向量维度较大，典型值为65536。因此第二代FHE运算的并行度很高，比较适合真实场景中对同态计算速度要求高的情形。

编码并非仅仅将向量中的数值直接填入多项式系数中，那样就不满足同态乘法的性质了。

可以看出，我们可以利用向量值以及其位置关系，构造点值多项式，由此，考虑到消息可以直接作为点值多项式中的点，在根据消息构建明文多项式时可以使用FFT或者NTT。

CKKS的编码：

考虑到消息为复数域上的元素组成，我们利用FFT构建CKKS的明文多项式

取共轭是因为代入m的自变量实际上也是两两共轭（1与5，3与7），因此，结果的共轭性是由自变量而来的，构建的多项式系数就为实数；

加入精度是为了减小多项式系数取整时产生的误差，由于CKKS属于近似计算，所以其结果的近似程度主要由△决定，在应用中，△可以取到。

BGV与BFV的编码类似，只是由于两者的消息均为整数，因此，直接使用NTT即可

1.4.2重线性化

重线性化即密钥替换，它主要被用于二代算法中同态乘法的部分，将同态乘后的密文恢复为RLWE密文的形式，从而便于进一步的同态计算或者解密操作。

假设存在两个密文,进行一次乘法计算后，得到密文(可以将两个密文视为两个多项式相乘）

可以看到使用重线性化可以将密文的形式转变为RLWE的密文形式，但同时也增大了噪声（）。对于这一点可以使用decompose对f进行分解，从而减小此处的误差增长.

但是对于密文其他部分也需要进行相应处理（例如密钥rlk中的要使用Pow处理）。

1.4.3噪声缩小问题

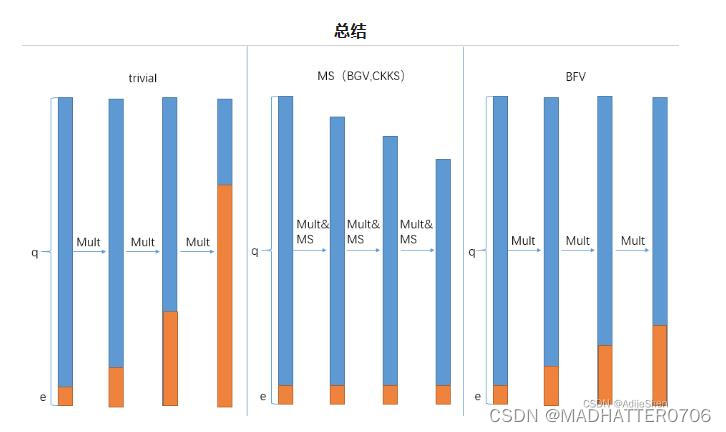
模数替换Modulus Switching（CKKS，BGV）

二代算法中，CKKS与BGV算法通过模数替换缩小噪声，二者都是通过缩小模数，进而缩小整个密文来实现减小噪声。

这里以BGV算法的模数替换为例，展示其缩小噪声的效果。

CKKS的模数缩减过程与BGV的相似，但考虑到CKKS近似计算的特点，模数缩减中产生的微小噪声还是会影响解密结果（CKKS的解密过程会保留噪声，直接将噪声项作为了解密后明文的一部分）。

Scale Invariant（BFV）

BFV算法不使用模数缩减来减小噪声，而是通过直接改变密文来实现的。

假设BFV经过同态乘法后的密文为,那么经过处理后的密文为,

其中BFV算法中对应的明文形式为，

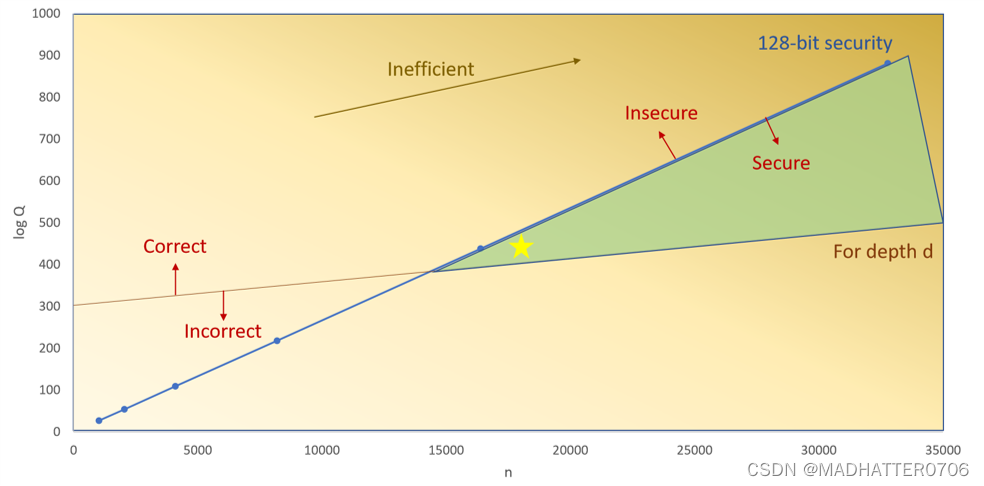
1.4.4参数与效率

下图为CKKS算法中，安全性以及效率与参数的关系图，其中n为多项式最大阶数，Q为模数。