2024年全国大学生数学建模D题-反潜航空深弹命中概率问题参考代码及思路

 ✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，代码获取、论文复现及科研仿真合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

🔥 内容介绍

应用深水炸弹（简称深弹）反潜，曾是二战时期反潜的重要手段，而随着现代军事技术的发展，鱼雷已成为现代反潜作战的主要武器。但是，在海峡或浅海等海底地形较为复杂的海域，由于价格低、抗干扰能力强，仍有一些国家在研究和发展深水炸弹反潜技术。反潜飞机攻击水下目标前，先由侦察飞机通过电子侦察设备发现水下潜艇目标的大致位置，然后召唤反潜飞机前来进行攻击。当潜艇发现被侦察飞机电子设备跟踪时，通常会立即关闭电子设备及发动机，采取静默方式就地隐蔽。本问题采用目标坐标系：潜艇中心位置的定位值在海平面上的投影为原点 𝑂，正东方向为 𝑋 轴正向，正南方向为 𝑌 轴正向，垂直于海平面向下方向为 𝑍 轴正向。正北方向顺时针旋转到潜艇航向的方位角记为 𝛽，假定在一定条件下反潜攻击方可获知该航向（见图 1）。

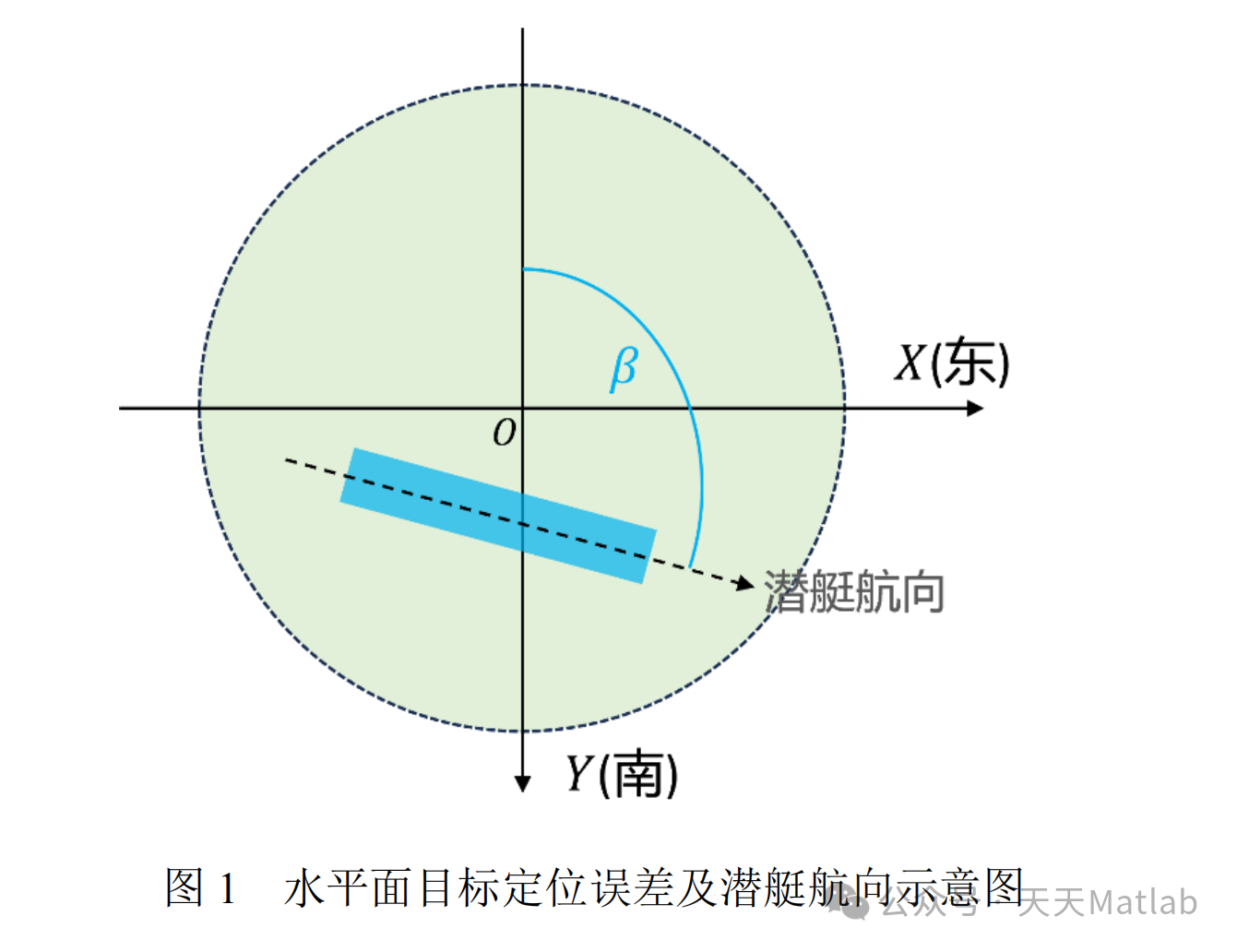
将潜艇主体部分简化为长方体，深弹在水中垂直下降。假定深弹采用双引信（触发引信 +定深引信）引爆，定深引信事先设定引爆深度，深弹在海水中的最大杀伤距离称为杀伤半径。深弹满足以下情形之一，视为命中潜艇：(1) 航空深弹落点在目标平面尺度范围内，且引爆深度位于潜艇上表面的下方，由触发引信引爆；

(2) 航空深弹落点在目标平面尺度范围内，且引爆深度位于潜艇上表面的上方，同时潜艇在深弹的杀伤范围内，由定深引信引爆；

(3) 航空深弹落点在目标平面尺度范围外，则到达引爆深度时，由定深引信引爆，且此时潜艇在深弹的杀伤范围内。请建立数学模型，解决以下问题：

问题 1 投射一枚深弹，潜艇中心位置的深度定位没有误差，两个水平坐标定位均服从正态分布。分析投弹最大命中概率与投弹落点平面坐标及定深引信引爆深度之间的关系，并给出使得投弹命中概率最大的投弹方案，及相应的最大命中概率表达式。针对以下参数值给出最大命中概率：潜艇长 100 m，宽 20 m，高 25 m，潜艇航向方位角为 90 ∘，深弹杀伤半径为 20 m，潜艇中心位置的水平定位标准差 𝜎 = 120 m，潜艇中心位置的深度定位值为 150 m.

问题 2 仍投射一枚深弹，潜艇中心位置各方向的定位均有误差。请给出投弹命中概率的表达式。

针对以下参数，设计定深引信引爆深度，使得投弹命中概率最大：潜艇中心位置的深度定位值为 150 m，标准差 𝜎𝑧 = 40 m，潜艇中心位置实际深度的最小值为 120 m，其他参数同问题 1。

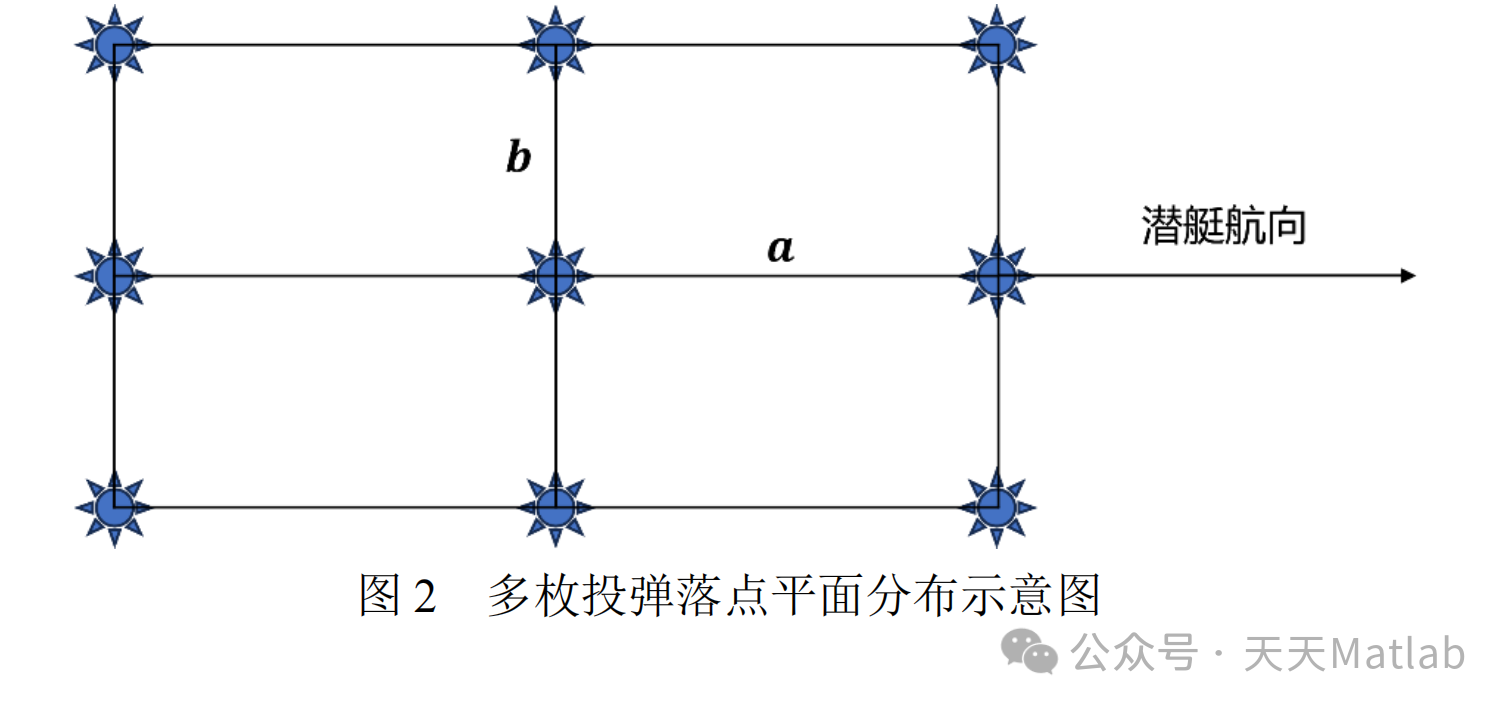
问题 3 由于单枚深弹命中率较低，为了增强杀伤效果，通常需要投掷多枚深弹。若一 架反潜飞机可携带 9 枚航空深弹，所有深弹的定深引信引爆深度均相同，投弹落点在平面上 呈阵列形状（见图 2）。在问题 2 的参数下，请设计投弹方案（包括定深引信引爆深度，以 及投弹落点之间的平面间隔），使得投弹命中（指至少一枚深弹命中潜艇）的概率最大。

📣 赛题分析

建立模型：

1. 假设潜艇中心位置的水平坐标 服从二维正态分布，均值为标准差为。

2. 深弹落点在目标平面尺度范围内，即落在以潜艇中心为圆心，半径为 （潜艇长度的一半）的圆内。

3. 根据深弹的引爆深度和潜艇的深度，计算命中概率。

解题步骤：

1. 确定深弹落点的概率密度函数。

2. 根据深弹的杀伤半径和潜艇的尺寸，确定触发引信和定深引信的引爆条件。

3. 利用积分计算在不同落点和引爆深度下的命中概率。

4. 通过优化方法（如梯度上升或计算机模拟）找到使命中概率最大的落点和引爆深度。

最大命中概率表达式：由于涉及到正态分布和几何概率，具体的表达式可能需要通过数值积分或模拟来得到。

投弹方案：找到使命中概率最大的投弹落点坐标 和定深引信引爆深度 𝑧0。

问题 2

建立模型：

1. 考虑潜艇中心位置在三个方向上都有定位误差，即 服从三维正态分布。

2. 根据深弹的杀伤半径和潜艇的尺寸，确定引爆条件。

解题步骤：

1. 确定三维正态分布的概率密度函数。

2. 计算在不同引爆深度下的命中概率。

3. 设计优化算法，找到使命中概率最大的引爆深度。

命中概率表达式：这个表达式会涉及到三维正态分布的积分，可能需要通过数值方法来计算。

定深引信引爆深度：找到使命中概率最大的引爆深度 𝑧0z0。

问题 3

建立模型：

1. 考虑多枚深弹的投掷，落点在平面上呈阵列形状。

2. 确定每枚深弹的定深引信引爆深度相同。

解题步骤：

1. 确定单枚深弹的命中概率。

2. 通过模拟或优化算法，设计投弹方案，包括引爆深度和落点之间的平面间隔。

3. 计算至少一枚深弹命中的概率。

投弹方案：找到使至少一枚深弹命中的概率最大的投弹方案，包括定深引信引爆深度和落点之间的平面间隔。

🔗 参考代码

智能优化算法       神经网络预测       雷达通信       无线传感器        电力系统

信号处理              图像处理               路径规划       元胞自动机        无人机 

物理应用        机器学习

🎈 部分理论引用网络文献，若有侵权联系博主删除