【数学】算术平均、几何平均、调和平均的区别与使用

算术平均（Arithmetic Mean）

算术平均是最常见的平均值计算方法。所有数据点的总和除以数据点的数量。

用途

算术平均适用于大多数普通的平均值计算场景，如测量数据、考试成绩等。它能很好地反映数据的中心趋势，特别是在数据分布较为均匀的情况下。 

优点:

• 简单直观，容易理解和计算。
• 在数据分布均匀时，能很好地代表整体情况。

缺点:

• 对极值（即非常大或非常小的值）非常敏感，可能导致失真。

几何平均 (Geometric Mean)

几何平均是通过计算所有数据点的乘积，然后取其n次方根得到的平均值。  

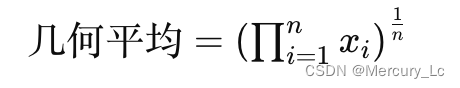
用途:

几何平均常用于计算增长率（如投资回报率、人口增长率等）和比例变化，因为它可以更好地处理乘法效应和相对变化。

优点:

• 能更准确地反映数据的相对变化。
• 对于处理成比例的数据或涉及乘法关系的数据特别有效。

缺点:

• 不能处理负数或零值，因为这些值会使乘积为负或为零，从而无法取根。
• 计算过程相对复杂。

调和平均 (Harmonic Mean) 

调和平均是数据点倒数的平均值的倒数。

用途:

调和平均在计算速度、密度等比率型数据时特别有用。例如，计算平均速度、平均每单位成本等。

优点:

• 对于处理速率、比率等数据特别有效。
• 能很好地处理数据集中某些小值的情况。

缺点:

• 对于极小值非常敏感，会被非常小的数据点拉低。
• 不能处理为零的数据点，因为零的倒数是无穷大。

总结

• 算术平均适用于一般情况，特别是在数据分布均匀且没有极端值时。
• 几何平均适用于计算比例变化和乘法关系的数据，例如 SPEC CPU 中多个 Benchmarks 的结果聚合成一个值，这里每一个数值本身是比例的关系。
• 调和平均适用于处理速率和比率型数据，如平均速度和每单位成本。