深入理解L1L2正则化

https://zhuanlan.zhihu.com/p/40563426（这是数据归一化的连接）

这篇文章是在知乎上看到的，讲解的相当精彩，在这里手动敲一遍，拟深刻理解正则化的数学原理，与君共勉。

Regularization：正则化

是机器学习中常用的一种技术，主要目的是：

控制模型复杂度，减小过拟合。

最基本的正则化方法是在原目标（代价）函数的基础上加上一个正则项，对复杂度高的模型进行“惩罚”，数学表达式为：

其中:

X：训练样本

Y：训练样本对应的标签

w：权重系数

J()：目标函数

：为惩罚项，可以理解为模型“规模”的一种度量

：控制正则化的强弱

不同的对不同的权重w有着不同的“偏好”，因而会产生不同的效果

最常用的有两种：L1范数和L2范数，带入之后得到：

L1正则化和L2正则化

我旨在深入理解L1L2正则化的背后的数学原理，并对L1正则化为何会产生稀疏性效果做出解释，接下来，welcome to match domin

---

一 L1、L2正则化来源推导

L1L2的推导可以从两个角度：

• 带约束条件的优化求解（拉格朗日乘子法）
• 最大后验概率

1.1 基于约束条件的最优化

对于模型权重系数w的求解释通过最小化目标函数实现的，也就是求解：

首先，模型的复杂度可以用VC来衡量。通常情况下，模型VC维与系数w的个数成线性关系：即：

w数量越多，VC越大，模型越复杂

为了限制模型的复杂度，我们要降低VC，自然的思路就是降低w的数量，即：

让w向量中的一些元素为0或者说限制w中非零元素的个数。我们可以在原优化问题上加入一些优化条件：

其中约束条件中的||w||0是指L0范数，表示的是向量w中非零元素的个数，让非零元素的个数小于某一个C，就能有效地控制模型中的非零元素的个数，但是这是一个NP问题，不好解，于是我们需要做一定的“松弛”。为了达到我们想要的效果（权重向量w中尽可能少的非零项），我们不再严格要求某些权重w为0，而是要求权重w向量中某些维度的非零参数尽可能接近于0，尽可能的小，这里我们可以使用L1L2范数来代替L0范数，即：

注意哈：这里使用L2范数的时候，为了后续处理（其实就是为了优化），可以对进行平方，只需要调整C的取值即可。

然后我们利用拉式乘子法求解：

其中这里的是拉格朗日系数，>0，我们假设的最优解为，对拉格朗日函数求最小化等价于：

上面和

等价。所以我们这里得到对L1L2正则化的第一种理解：

L1正则化  在原优化目标函数中增加约束条件

L2正则化  在原优化目标函数中增加约束条件

1.1 基于最大后验概率估计

在最大似然估计中，是假设权重w是未知的参数，从而求得对数似然函数（取了log）：

从上式子可以看出：假设的不同概率分布，就可以得到不同的模型。

若我们假设：

的高斯分布，我们就可以带入高斯分布的概率密度函数：

上面的C为常数项，常数项和系数不影响我们求解的解，所以我们可以令

我们就得到了Linear Regursion的代价函数。

在最大化后验概率估计中，我们将权重w看做随机变量，也具有某种分布，从而有：

同样取对数：

可以看出来后验概率函数为在似然函数的基础上增加了logP(w)，P（w）的意义是对权重系数w的概率分布的先验假设，在收集到训练样本{X，y}后，则可根据w在{X，y}下的后验概率对w进行修正，从而做出对w的更好地估计。

若假设的先验分布为0均值的高斯分布，即

则有：

可以看到，在高斯分布下

的效果等价于在代价函数中增加L2正则项。

若假设服从均值为0，参数为a的拉普拉斯分布，即：

则有：

可以看到，在拉普拉斯分布下logP(w)的效果等价在代价函数中增加L1正项。

故此，我们得到对于L1，L2正则化的第二种理解：

L1正则化可通过假设权重w的先验分布为拉普拉斯分布，由最大后验概率估计导出。

L2正则化可通过假设权重w的先验分布为高斯分布，由最大后验概率估计导出。

---

二 L1、L2正则化效果分析

 

为什么L1就能替代L0范数，其中的数学原理到底是啥？

what is 龙格现象？解决方法？

在数值分析领域中，龙格现象是在一组等间插值点上使用具有高次多项式的多项式插值时出现的区间边缘处的振荡问题。 它是由卡尔·龙格（Runge）在探索使用多项式插值逼近某些函数时的错误行为时发现的。[1]这一发现非常重要，因为它表明使用高次多项式插值并不总能提高准确性。 该现象与傅里叶级数近似中的吉布斯现象相似。

                                                                             

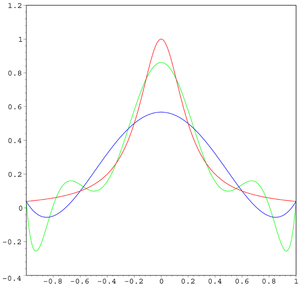
                                红色曲线是龙格函数，蓝色曲线是 5 阶多项式，绿色曲线是 9 阶多项式。随着阶次的增加，误差逐渐变大

解决方法

使用切比雪夫节点代替等距点可以减小震荡，在这种情况下，随着多项式阶次的增加最大误差逐渐减小。这个现象表明高阶多项式通常不适合用于插值。使用分段多项式样条可以避免这个问题。如果要减小插值误差，那么可以增加构成样条的多项式的数目，而不必是增加多项式的阶次。