计算机图形学6--讨论多边形

一、前言

多边形：数学上定义为由三个或更多个称为顶点的坐标位置描述的平面图形，这些顶点由称为多边形的边顺序连接；

根据定义，一个多边形的所有顶点必须在同一个平面上且所有的边之间无交叉，例如三角形、矩形、八边形和十六边形等。

有时，任意有封闭折线边界的平面图形暗指一个多边形，而若没有交叉边则称为标准多边形或简单多边形；

---

在计算机图形学的应用中，用于指定多边形的一组顶点并不严格在一个平面上。这可能由数值计算的舍入误差、对坐标位置的选择错误或更一般地由于使用一组多边形面片逼近曲面而引起。纠正该问题的一种方法是简单地将指定曲面网分割成三角形。但有时必须保留网格面片的原始形状，以便开发用平面图形逼近非平面多边形的方法。

---

二、多边形分类

凸多边形：如果一个多边形的所有内角均小于180°，则该多边形为凸多边形。凸多边形的一个等价定义是它的内部完全在它的任意一边及其延长线的一侧。
凹多边形：不是凸多边形的多边形就是凹多边形。

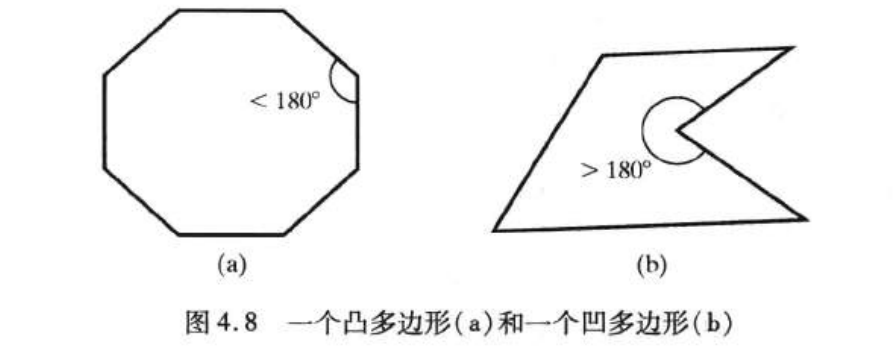
凹多边形的填充算法和其它图形子程序的实现比较复杂，因此在处理前常将凹多边形分割成一组凸多边形以便提高效率。和其它的多边形预处理算法一样，凹多边形的分割一般也不包括在图形函数库中。OpenGL等图形软件包要求所有的填充多边形为凸多边形。有些系统仅接受三角形填充区，这将大大简化许多显示算法。

---

三、识别凹多边形

我们可以将凹多边形的特征中的任意一个作为基础来设计识别算法：

• 凹多边形中至少有一个内角大于180°；
• 凹多边形某些边的延长线会与其它边相交，且有时一个内点之间的连线会与多边形边界相交；

如果为每一条变建立一个向量，则可以使用相邻边的叉积来测试凹凸性；

• 多边形的所有向量叉积均同号，则该多边形为凸多边形；
• 多边形的某些叉积取正值而另外一些取负值，则该多边形为凹多边形；如图4.9所示；

识别凹多边形的另一个方法是观察多边形顶点位置与每条边延长线的关系，如果有些顶点在某一边的延长线的一侧，而其它一些顶点在另一侧，则该多边形为凹多边形；

参考文章

---

四、分割凹多边形

4.1、向量法

对于分割凹多边形的向量方法，我们首先要形成边向量，多边形转换为向量：

• 选定一个合适的坐标系；
• 将各边依此标好箭头，表示向量方向；
• 将边的起点移动的原点，向量的坐标表示即为箭头端的坐标；

接着按多边形边界顺序计算连续的边向量的叉积。如果有些叉积的Z分量为正而另一些为负，则多边形为凹多边形；否则多边形为凸多边形。如果有一个叉积的Z分量为负值，那么多边形为凹，且可沿叉积中第一边分量的直线进行切割。
例如：图4.10给出了一个由6个顶点的凹多边形

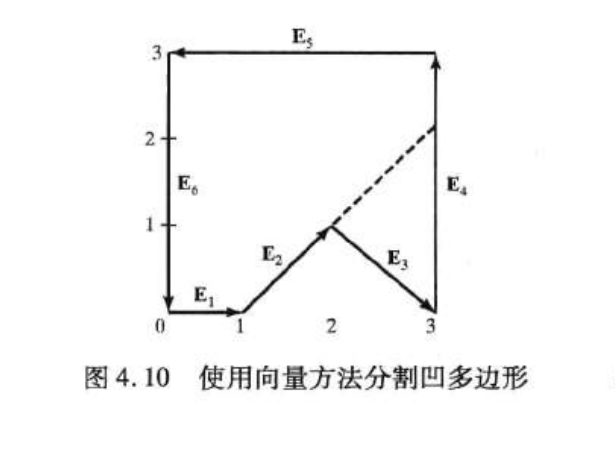
该多边形的边向量表示为：
E₁ = (1,0,0)
E₂ = (1,1,0)
E₃ = (1,-1,0)
E₄ = (0,3,0)
E₅ = (-3,0,0)
E₆ = (0,-3,0)
这里的Z分量均为0，因为所有边均在xy平面上。两个连续的边向量的叉积E_i x E_j是垂直于xy平面的向量，所以叉积的结果形式都为(0,0,x),其分量等于E_ixE_jy - E_iyE_jx，所以：
E₁ x E₂ = (0,0,1)
E₂ x E₃ = (0,0,-2)
E₃ x E₄ = (0,0,3)
E₄ x E₅ = (0,0,6)
E₅ x E₆ = (0,0,6)
E₆ x E₁ = (0,0,2)
因为叉积E₂ x E₃的Z分量为负，所以我们沿着向量E₂所在的直线分割多边形。 该边的直线方程中斜率为1而y轴截距为-1。然后我们可以确定该直线和其它边的交点来将多边形分割成两片。其它边叉积不为负，所以得到的两个多边形均为凸多边形。

---

4.2、旋转法

给多边形的顶点依此编号，依此将顶点V_k移到坐标系原点。然后顺时针旋转多边形，使下一个顶点V_k+1落在x轴上。

如果再下一个顶点V_k+2位于x轴下面，则多边形为凹。然后利用x轴将多边形分割成两个新多边形，并对这两个新多边形重复使用凹测试，知道多边形中所有顶点均经过测试。

---

五、凸多边形分割成三角形集

一旦有了一个凸多边形的顶点集，我们就可以将其变成一组三角形。

这通过将任意顺序的三个连续顶点定义为一个新多边形（三角形）来实现。然后将三角形的中间顶点从多边形原顶点队列中删除。接着使用相同的过程处理修改后的顶点队列来分出另一个三角形。这种分割一直进行到原多边形仅留下三个顶点，它们定义三角形集合中的最后一个。

凹多边形也可以使用这种方法分割为三角形集，但要求连接所选的第一、三顶点之间的线段不穿过多边形的凹区域，并且每次三顶点形成的内角小于180°（一个凸角）。

5.1、内-外测试

各种图形处理常需要鉴别对象的内部区域。识别简单对象如凸多边形、圆或椭圆的内部时常是一个很容易的事。但有时我们必须处理较复杂的对象。例如，我们可能描述一个图4.12所示的有相交边的复杂填充区。
在该形状中，xy平面上哪一部分为对象边界的“内部”、哪一部分为“外部”并不总是一目了然的。奇偶规则和非零环绕数规则是识别平面图形内部区域的两种常用方法。对于多边形和圆等简单对象，两种方法给出了相同的结果；但对于比较复杂的形状，两种方法可能会产生如图4.12所示的补贴的内部和外部区域。

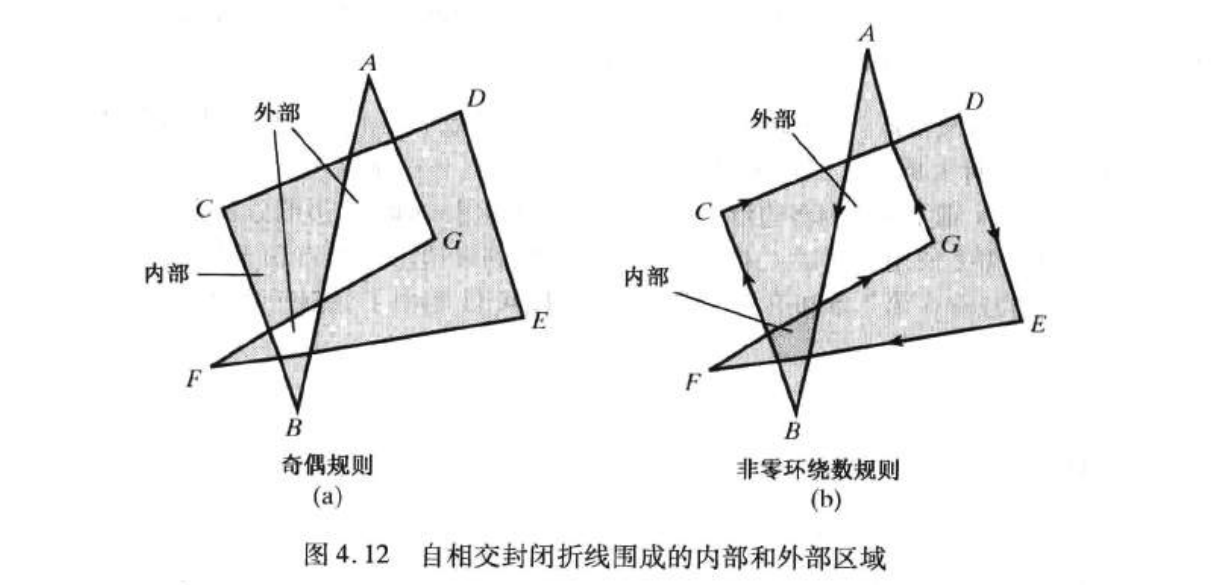
奇偶规则
该规则从任意位置P到对象坐标范围以外的远点画一条概念上的直线（射线），并统计沿该射线与各边的交点数目

• 假设与这条射线相交的多边形边上为奇数，则P是内部点；
• 假设与这条射线相交的多边形边上为偶数，则P是外部点；

为了得到精确的相交边数，必须确认所画的直线不与任何多边形顶点相交。图4.12（a）给出了奇偶规则得到的自相交封闭折线的内部和外部区域。

---

非零环绕数规则
该方法统计多边形以逆时针方向环绕某一特定点的次数。这个数称为环绕数，二维对象的内部点是那些具有非零值环绕数的点。

在对多边形应用非零环绕数规则时，将环绕数初始化为零。设想从任意位置P到对象坐标范围外的远处一点画一条射线。所选择的射线不能与多边形的任何顶点相交。当从P点沿射线方向移动时，统计穿过该射线的边的方向。每当多边形从右到左穿过射线时，边数加1；从左到右时，边数减1.在所有穿过的边都已计数后，环绕数的最终值决定了P的相对位置。假如环绕数为非零，则P将定义为内部点，否则P是外部点。图4.12（b）给出了非零环绕数规则得到的自相交封闭折线的内部和外部区域。