【随机过程-学习笔记】(1)–马尔科夫链的定义与转移概率与绝对概率
一、马尔科夫链
- 马尔科夫链的出现
具有马氏性,是指今天与昨天有关,但与前天无关(广义理解)。 p ( x t ∣ x t − 1 , x t − 2 , . . . x t − n ) = p ( x t ∣ x t − 1 ) p(x_t|x_{t-1},x_{t-2},...x_{t-n})=p(x_t|x_{t-1}) p(xt∣xt−1,xt−2,...xt−n)=p(xt∣xt−1), x t x_t xt为今天, x t − 1 x_{t-1} xt−1为昨天,因此, x t x_t xt只与昨天有关。
t 0 t_0 t0时刻所在的样本空间( Ω \Omega Ω),在马尔科夫中被称为状态空间,并且 t 0 t_0 t0中的各样本点 X t 0 X_{t_0} Xt0是随机变量,可以随机选取、也可以连续选取;

然后, t 0 t_0 t0与 t 1 t_1 t1之间,是时间空间,具体的时间间隔,可以随机选取、也可以连续选取;
因此,具体的选取过程如下:
① 状态空间=>离散,时间空间=>离散,称为马氏科夫链;↓

② 状态空间=>离散,时间空间=>连续,称为马尔科夫过程;↓
③ 状态空间=>连续,时间空间=>离散,称为马尔科夫列;
④ 状态空间=>连续,时间空间=>连续,称为扩散过程。 - 马氏科夫链
① 马氏科夫链的解释
任意取第 n + 1 {n+1} n+1步,如图:
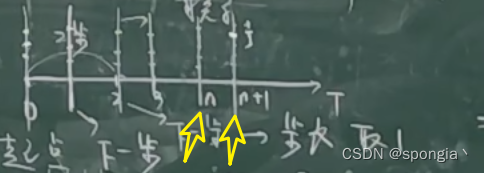
那么两步之间的联系可以被表示为:
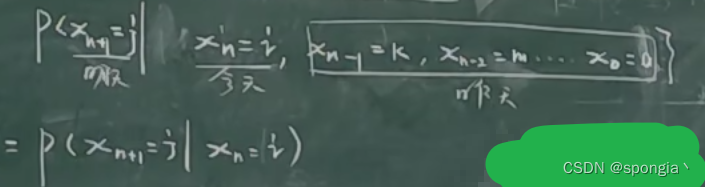
其中,时刻为 t n t_n tn和 t n + 1 t_{n+1} tn+1时,都取离散的随机变量,因此{ X n , n ∈ N X_n,n\in N Xn,n∈N}的过程被称为马尔科夫链,写法上,表示为
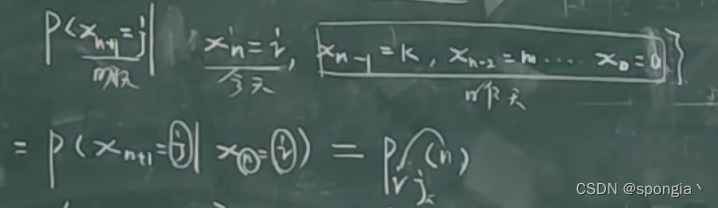
② 转移与转移概率

而,转移概率,则被表示为:

若知道,如果发生 p ( x n + 1 ) p(x_{n+1}) p(xn+1)的前提是已经发生 p ( x n ) p(x_{n}) p(xn),因此从状态 i i i转移到状态 j j j,就需要有 p ( x n ) p(x_{n}) p(xn)为基础,同时还要考虑转移概率 p ( x i j ( n ) ) p(x_{ij}(n)) p(xij(n)),才能够得到 p ( x n + 1 ) p(x_{n+1}) p(xn+1)。进一步的,可以得出:
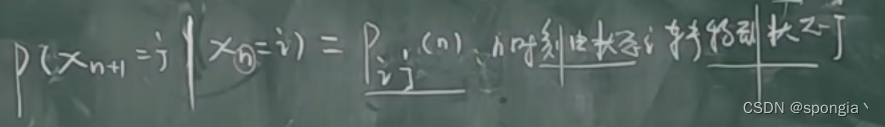
那么,状态转移概率 p ( x i j ( n ) ) p(x_{ij}(n)) p(xij(n))便理解为: n n n时刻由状态 i i i转移到状态 j j j。
③ 相对概率与绝对概率
需要注意,转移概率不是状态 i i i的概率,也不是状态 j j j的概率,反应出的是过程,是指走一步的动态。
而面对与时间无关(时齐)的情况下,即静止状态时,发生的概率,是指n时刻下取各个值的概率。因为静止时,各值是离散的,随机变量 X n X_n Xn的取值则包含若干的,例如包含1,2,3,共3个状态,那么这些状态的概率被表称为绝对概率,也是静止概率,表示为 π i ( n ) \pi _i(n) πi(n): n n n时刻 p ( X n = i ) p(X_n=i) p(Xn=i)。
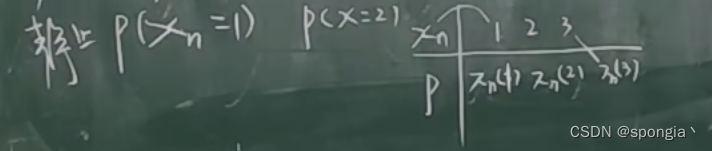
即 π n ( 1 ) \pi _n(1) πn(1)、 π n ( 2 ) \pi _n(2) πn(2)、 π n ( 3 ) \pi _n(3) πn(3)。指 n n n时刻包含的全部状态。

那么在静态下,由状态n到状态n+1,能够得出n+1状态下的转移概率矩阵。
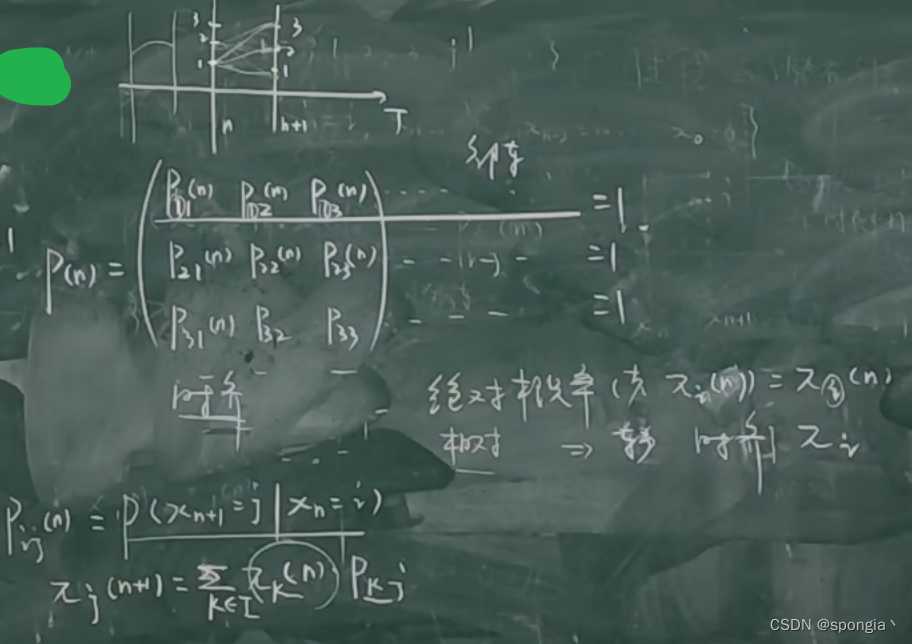
有时间参与时,需要加入 n n n,即绝对概率 P ( n ) P(n) P(n)。时齐时,没有 n n n的参与,为相对概率 P P P。
























 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










