图灵程序丛书 —《数据科学入门》— Ch8 梯度下降法

Ch8 梯度下降法

此系列记录《数据科学入门》学习笔记

8.2 梯度下降的思想

梯度下降法只能找到局部最优解，而不是全局最优解；

当有多个全局最优解时,可以通过多尝试一些初始点来重复搜索；

当一个函数没有最小点时，计算可能会陷入死循环。

8.2 估算梯度

def sum_of_squares(v):
    return sum(v_i ** 2 for v_i in v)

# 单变量函数的导数可通过差商来定义
def difference_quotient(f, x, h):
    return (f(x + h) - f(x)) / h

def square(x):
    return x * x

def derivative(x):
    return 2 * x


# python 无法直接运算极限，但可以通过计算一个很小的变动e的差商来估算微分
import matplotlib.pyplot as plt
from pylab import *
from functools import partial

# 固定f=x^2,h=0.00001
derivative_estimate = partial(difference_quotient, square, h=0.00001)
mpl.rcParams['axes.unicode_minus']=False
mpl.rcParams['font.sans-serif'] = ['SimHei']  
x = range(-10, 10)
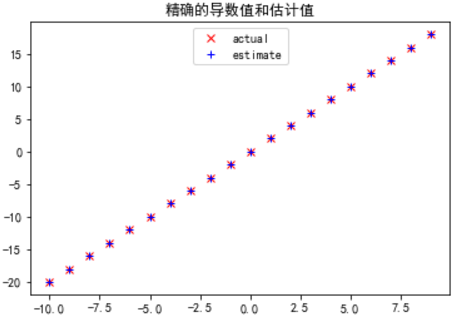
plt.title('精确的导数值和估计值')
plt.plot(x, list(map(derivative, x)), 'rx', label='actual')
plt.plot(x, list(map(derivative_estimate, x)), 'b+', label='estimate')
plt.legend(loc=9)
plt.show()

# 计算偏导数
# 把导数看成是其第i个变量的函数，其他变量保持不变，以此来计算他的第i个偏导数
def partial_difference_quotient(f, v, i, h):
    w = [v_j + (h if j == i else 0) for j, v_j in enumerate(v)]     #只对v的第i个元素加h
    return (f(w) - f(v)) / h

def estimate_gradient(f, v, h):
    return [partial_difference_quotient(f, v, i, h) for i, _ in enumerate(v)]

"""
‘差商估算法’的主要缺点是计算代价很大，如果v长度为n，那么estimate_gradient为了计算f需要2n个不同的输入变量。
如果需要反复计算题都，那需要做很多额外的工作
"""

8.3 使用梯度

# 用梯度方法可以从三维向量中找到最小值
# 可以先找出随机初始点，并在梯度的反方向以小步逐步前进，知道梯度变得非常小
"""下列程序总是止于一个非常接近[0， 0， 0]的v值，tolerance的值设定的越小， v的值就越接近[0， 0， 0]"""
import random
import numpy as np

def step(v, direction, step_size):
    return [v_i + step_size * direction_i for v_i, direction_i in zip(v, direction)]

# 平方函数的梯度
def sum_of_squares_gradient(v):
    return [2 * v_i for v_i in v]

def distance(v, w):
    return np.sqrt(sum((v_i - w_i) ** 2 for v_i, w_i in zip(v, w)))

# 随机选择三维向量的初始点
v = [random.randint(-10, 10) for i in range(3)]
tolerance = 0.0000001

while True:
    gradient = sum_of_squares_gradient(v)
    next_v = step(v, gradient, -0.01) 
    if distance(next_v, v) < tolerance:
        break
    v = next_v
print(v)
# [-3.688294692016085e-06, -2.868673649345841e-06, -1.6392420853404806e-06]

8.4 选择正确步长

选择合适的步长更像艺术而非科学，主流方法有：
1、使用固定步长；
2、随着时间增长逐步减小步长；
3、在每一步中通过最小化目标函数值来选择步长。此方法看上去不错，但是计算代价也最大。
可以尝试一系列步长，并选出使目标函数值最小的的那个步长来求其近似值：step_sizes = [100, 10, 1, 0.1, 0.01, 0.001, 0.0001, 0.00001]

# 某些步长可能会导致函数的输入无效，故需要创建一个对无效输入值返回无限制的‘安全应用’函数（即这个值永远不会成为任何函数的最小值）
def safe(f):
    """return a function that is the same as f, except that it outputs infinity whenever f produces an error"""
    def safe_f(*arg, **kwargs):
        try:
            return f(*args, **kwargs)
        except:
            return float('inf')  # python 里的‘无限值’
    return safe_f

8.5 综合

# 批量梯度下降法（batch gradient descend），因为在每一步梯度计算中，他都会搜索整个数据集（target_fn代表整个数据集的残差）

def minimize_batch(target_fn, gradient_fn, theta_0, tolerance=0.000001):
    """use gradient descent to find theta that minimizes target fuction"""
    
    step_sizes = [100, 10, 1, 0.1, 0.01, 0.001, 0.0001, 0.00001]
    
    theta = theta_0                     # 设定theta为初始值
    target_fn = safe(target_fn)         # target_fn的安全版
    value = target_fn(theta)            # 试图最小化的值
    
    while True:              # while true为死循环，需要用break来退出
        gradient = gradient_fn(theta)
        next_thetas = [step(theta, gradient, -step_size) for step_size in step_sizes]
    
    # 选择一个使残差函数最小的值
    next_theta = min(next_thetas, key=target_fn)
    next_value = target_fn(next_theta)
    
    # 当‘收敛’时停止
    if abs(value - next_value) < tolerance:
        return theta
    else:
        theta, value = next_theta, next_value


# 最大化某个函数值 = 最小化这个函数的负值

def negate(f):
    """return a function that for any input x returns -f(x)"""
    return lambda *args, **kwargs: -f(*args, **kwargs)

def negate_all(f):
    """the same when f returns a list of numbers"""
    return lambda *args, **kwargs: [-y for y in f(*args, **kwargs)]

def maximize_batch(target_fn, gradient_fn, theta-0, tolerance=0.000001):
    return minimize_batch(negate(target_fn), negate_all(gradient_fn), theta_0)

8.6 随机梯度下降法(stochastic gradient descent)¶

残差函数往往具有可加性，意味着整个数据集上的预测残差刚好是每个数据点预测残差之和。
每次仅计算一个点的梯度（并向前跨一步），反复计算直到到达停止点。
对于每一个数据点都会进行一步梯度计算，这种方法也许会在最小值附近一直循环下去，所以每当停止获得改进，我们都会减小步长并最终退出。

def in_random_order(data):
    """generator that returns the elements of data in random order"""
    indexes = [i for i, _ in enumerate(data)]      # 生成索引列表
    random.shuffle(indexes)                        # 随机打乱数据
    for i in indexes:                             # 返回序列中的数据
        yield data[i]

def minimize_stochastic(target-fn, gradient_fn, x, y, theta_0, alpha_0=0.01):
    
    def scalar_multipy(c, v):
        return [c * v_i for v_i in v]
    
    def vector_subtract(v, w):
        return [v_i - w_i for v_i, w_i in zip(v,w)]
        
    data = zip(x, y)
    theta = theta_0                               # 初始值设定
    alpha = alpha_0                               # 初始步长
    min_theta, min_value = None, float('inf')    # 迄今为止的最小值
    iterations_with_no_improvement = 0
    
    # 当循环超过100次仍然无改进，则停止循环
    while iterations_with_no_improvement < 100:
        value = sum(target_fn(x_i, y_i, theta) for x_i, y_i in data)
        
        if value < min_value:
            # 如果找到新的最小值，记住它，并返回到最初的步长
            min_theta, min_value = theta, value
            iterations_with_no_improvement =  0
            alpha = alpha_0
        else:
            # 尝试缩小步长，否则没有改进
            iterations_with_no_improvement += 1
            alpha *= 0.9
            
        # 在每个数据点上向梯度方向前进一步
        for x_i, y_i in in_random_order(data):
            gradient_i = gradient_fn(x_i, y_i, theta)
            theta = vector_substract(theta, scalar_multipy(alpha, gradient_i))
            
    return min_theta

def maximize_stochastic(target_fn, gradient_fn, x, y, theta_0, alpha_0=0.01):
    return minimize_stochastic(negate(target_fn), negate_all(gradient_fn), x, y, theta_0, alpha_0)

以上是Ch8的相关内容

2018.03.08   YR