机器学习入门教程——week 2

一、基础知识点

多元线性回归：

（1）给出一个多元参数的例子：

其中n表示特征的数量， 表示第i个训练样本， 表示第i个训练样本的第j个特征。假设公式hypothesis如下图所示：

（2）多元函数的代价函数为：

    

或者

（3）梯度下降

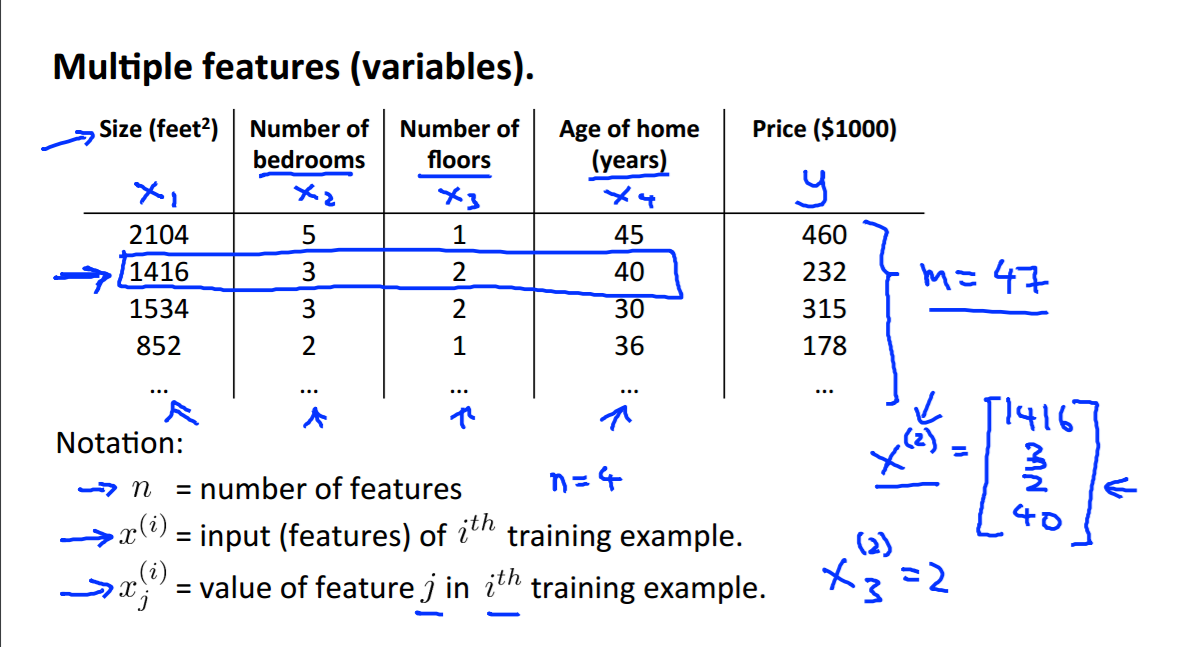
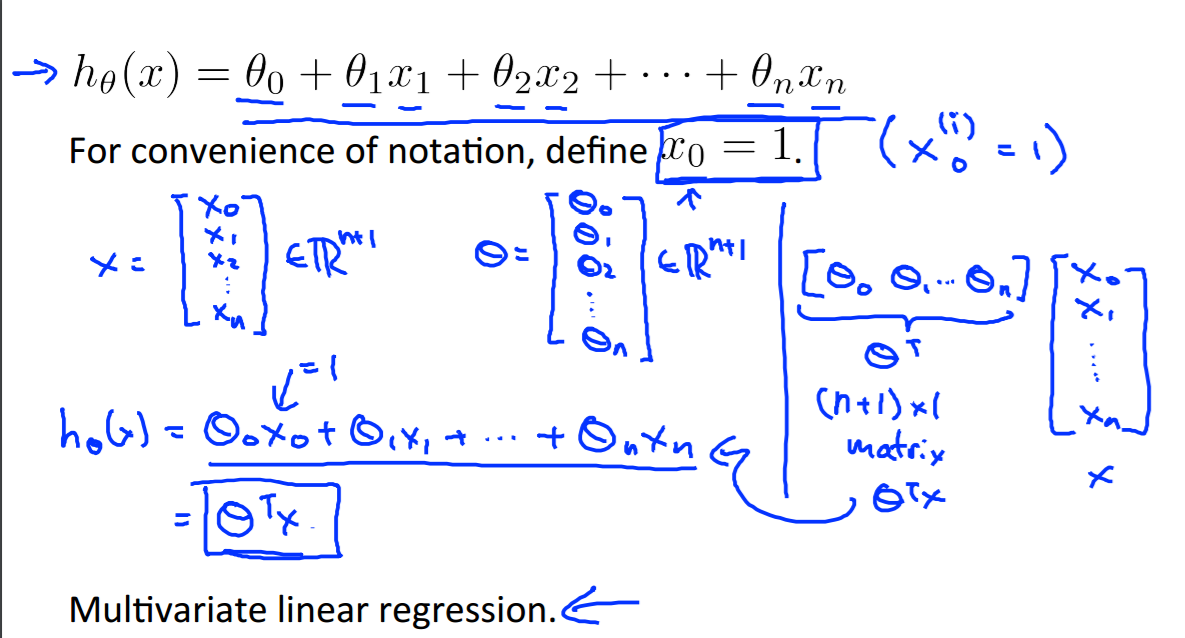
二、补充知识点

这两周主要是在做数据融合与智能分析的project，会去看一些有趣的机器学习方法，同时把它应用在实际问题中。

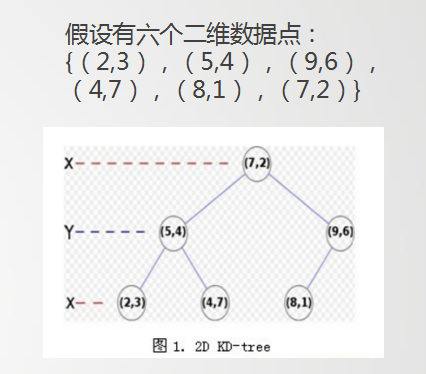
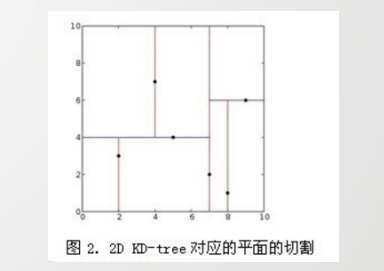
（1）近似最近邻算法：kd-tree

构建好一棵Kd-Tree后，下面给出利用Kd-Tree进行最近邻查找的算法：

举个简单的例子：

算法描述：

输入：Kd /* k-d tree类型*/
target /* 待查询数据点 */
输出 : nearest /* 最近邻数据结点 */
dist /* 最近邻和查询点的距离 */

1. 如果Kd是空的，则设dist为无穷大返回
2. 向下搜索直到叶子结点
pSearch = &Kd
while(pSearch != NULL)  {
pSearch加入到search_path中;
if(target[pSearch->split] <= pSearch->dom_elt[pSearch->split]) /* 如果小于就进入左子树 */
{
pSearch = pSearch->left;
}
else  {
pSearch = pSearch->right;
}
}
取出search_path最后一个赋给nearest
dist = Distance(nearest, target);
3. 回溯搜索路径
while(search_path不为空)  {
取出search_path最后一个结点赋给pBack
if(pBack->left为空 && pBack->right为空) /* 如果pBack为叶子结点 */
{
if( Distance(nearest, target) > Distance(pBack->dom_elt, target) )  {
nearest = pBack->dom_elt;
dist = Distance(pBack->dom_elt, target);
}
}
else {
s = pBack->split;
if( abs(pBack->dom_elt[s] - target[s]) < dist) /* 如果以target为中心的圆（球或超球），半径为dist的圆与分割超平面相交， 那么就要跳到另一边的子空间去搜索 */
{
if( Distance(nearest, target) > Distance(pBack->dom_elt, target) )  {
nearest = pBack->dom_elt;
dist = Distance(pBack->dom_elt, target);
}
if(target[s] <= pBack->dom_elt[s]) /* 如果target位于pBack的左子空间，那么就要跳到右子空间去搜索 */
pSearch = pBack->right;
else
pSearch = pBack->left; /* 如果target位于pBack的右子空间，那么就要跳到左子空间去搜索 */
if(pSearch != NULL)
pSearch加入到search_path中
}
}
}

假设数据集的维数为D，一般来说要求数据的规模N满足N»2^D，才能达到高效的搜索。所以这就引出了一系列对k-d树算法的改进：BBF算法

（2）kd树近邻搜索算法的改进：BBF算法

输入：以构造的kd树，目标点x；
输出：x 的最近邻
算法步骤如下：

1. 在kd树种找出包含目标点x的叶结点：从根结点出发，递归地向下搜索kd树。若目标点x当前维的坐标小于切分点的坐标，则移动到左子结点，否则移动到右子结点，直到子结点为叶结点为止。
2. 以此叶结点为“当前最近点”。
3. 递归的向上回溯，在每个结点进行以下操作：
   （a）如果该结点保存的实例点比当前最近点距离目标点更近，则更新“当前最近点”，也就是说以该实例点为“当前最近点”。
   （b）当前最近点一定存在于该结点一个子结点对应的区域，检查子结点的父结点的另一子结点对应的区域是否有更近的点。具体做法是，检查另一子结点对应的区域是否以目标点位球心，以目标点与“当前最近点”间的距离为半径的圆或超球体相交：
   如果相交，可能在另一个子结点对应的区域内存在距目标点更近的点，移动到另一个子结点，接着，继续递归地进行最近邻搜索；
   如果不相交，向上回溯。
4. 当回退到根结点时，搜索结束，最后的“当前最近点”即为x 的最近邻点。

    如果实例点是随机分布的，那么kd树搜索的平均计算复杂度是O（logN），这里的N是训练实例树。所以说，kd树更适用于训练实例数远大于空间维数时的k近邻搜索，当空间维数接近训练实例数时，它的效率会迅速下降，一降降到“解放前”：线性扫描的速度。

    也正因为上述k最近邻搜索算法的第4个步骤中的所述：“回退到根结点时，搜索结束”，每个最近邻点的查询比较完成过程最终都要回退到根结点而结束，而导致了许多不必要回溯访问和比较到的结点，这些多余的损耗在高维度数据查找的时候，搜索效率将变得相当之地下，那有什么办法可以改进这个原始的kd树最近邻搜索算法呢？

    从上述标准的kd树查询过程可以看出其搜索过程中的“回溯”是由“查询路径”决定的，并没有考虑查询路径上一些数据点本身的一些性质。一个简单的改进思路就是将“查询路径”上的结点进行排序，如按各自分割超平面（也称bin）与查询点的距离排序，也就是说，回溯检查总是从优先级最高（Best Bin）的树结点开始。

//KD树近邻搜索改进之BBF算法  
int kdtree_bbf_knn( struct kd_node* kd_root, struct feature* feat, int k,  
                    struct feature*** nbrs, int max_nn_chks )                  //2  
{                                               //200  
    struct kd_node* expl;  
    struct min_pq* min_pq;  
    struct feature* tree_feat, ** _nbrs;  
    struct bbf_data* bbf_data;  
    int i, t = 0, n = 0;  
  
    if( ! nbrs  ||  ! feat  ||  ! kd_root )  
    {  
        fprintf( stderr, "Warning: NULL pointer error, %s, line %d\n",  
                __FILE__, __LINE__ );  
        return -1;  
    }  
  
    _nbrs = (feature**)(calloc( k, sizeof( struct feature* ) )); //2  
    min_pq = minpq_init();   
    minpq_insert( min_pq, kd_root, 0 ); //把根节点加入搜索序列中  
  
    //队列有东西就继续搜，同时控制在t<200步内  
    while( min_pq->n > 0  &&  t < max_nn_chks )  
    {                   
        //刚进来时,从kd树根节点搜索,exp1是根节点   
        //后进来时,exp1是min_pq差值最小的未搜索节点入口  
        //同时按min_pq中父,子顺序依次检验,保证父节点的差值比子节点小.这样减少返回搜索时间  
        expl = (struct kd_node*)minpq_extract_min( min_pq );  
        if( ! expl )                                          
        {                                                     
            fprintf( stderr, "Warning: PQ unexpectedly empty, %s line %d\n",  
                    __FILE__, __LINE__ );                           
            goto fail;  
        }  
  
        //从根节点(或差值最小节点)搜索,根据目标点与节点模值的差值(小)  
        //确定在kd树的搜索路径,同时存储各个节点另一入口地址\同级搜索路径差值.  
        //存储时比较父节点的差值,如果子节点差值比父节点差值小,交换两者存储位置,  
        //使未搜索节点差值小的存储在min_pq的前面,减小返回搜索的时间.  
        expl = explore_to_leaf( expl, feat, min_pq );   
        if( ! expl )                                    
        {                                               
            fprintf( stderr, "Warning: PQ unexpectedly empty, %s line %d\n",  
                    __FILE__, __LINE__ );                     
            goto fail;                                    
        }                                               
  
        for( i = 0; i < expl->n; i++ )  
        {   
            //使用exp1->n原因:如果是叶节点,exp1->n=1,如果是伪叶节点,exp1->n=0.  
            tree_feat = &expl->features[i];  
            bbf_data = (struct bbf_data*)(malloc( sizeof( struct bbf_data ) ));  
            if( ! bbf_data )  
            {  
                fprintf( stderr, "Warning: unable to allocate memory,"  
                    " %s line %d\n", __FILE__, __LINE__ );  
                goto fail;  
            }  
            bbf_data->old_data = tree_feat->feature_data;  
            bbf_data->d = descr_dist_sq(feat, tree_feat); //计算两个关键点描述器差平方和  
            tree_feat->feature_data = bbf_data;  
  
            //取前k个  
            n += insert_into_nbr_array( tree_feat, _nbrs, n, k );//  
        }                                                  //2  
        t++;  
    }  
  
    minpq_release( &min_pq );  
    for( i = 0; i < n; i++ ) 
    {  
        bbf_data = (struct bbf_data*)(_nbrs[i]->feature_data);  
        _nbrs[i]->feature_data = bbf_data->old_data;  
        free( bbf_data );  
    }  
    *nbrs = _nbrs;  
    return n;  
  
fail:  
    minpq_release( &min_pq );  
    for( i = 0; i < n; i++ )  
    {  
        bbf_data = (struct bbf_data*)(_nbrs[i]->feature_data);  
        _nbrs[i]->feature_data = bbf_data->old_data;  
        free( bbf_data );  
    }  
    free( _nbrs );  
    *nbrs = NULL;  
    return -1;  
} 

三、学习收获

近两周对近似最近邻算法有了一定的了解，近似最近邻可以用于图像特征提取与匹配、海量数据最近邻查找、网页推荐系统等等，我是用来对二维位置数据点计算最近邻点，得到一条完整路径，与历史数据对比，分析出是否为异常路径。同时要求的octave编程也在进行，感觉对机器学习越来越有兴趣，因为应用非常的广泛，可以实现很多实际的事情。坚持下去~