关于小行星轨道问题解决方法的浅析（Matlab数学建模）

Etherious_Young

已于 2024-09-09 08:45:09 修改

阅读量2.2k

点赞数 26

分类专栏：数学建模文章标签：算法数学建模

于 2024-09-08 10:41:58 首次发布

本文链接：https://blog.csdn.net/NatsuD/article/details/142023157

版权

数学建模专栏收录该内容

4 篇文章

订阅专栏

摘要：天文学家要确定一颗小行星绕太阳运行的轨道，他在五个不同的时刻对这个星球进行了五次观测得出五组数据。基于此，他在轨道平面内建立了以太阳为原点的空间直角坐标系，现在根据其给出的数据，确定小行星轨道并画出，根据二次曲线理论，计算小行星椭圆轨道的重要参数，包括长半轴短半轴近日点距等，考虑合适的方法计算其近日点坐标，查阅二次曲线不变量的相关知识，尝试给出椭圆变换为最简方程形式的推导过程或证明。型最终运算结果较为准确，经核验结果可行性极高，图形结果直观简便，符合题目要求及现实情况。

关键词：小行星轨道问题近日点变换二次曲线不变量

1.问题重述

一天文学家要确定一颗小行星绕太阳运行的轨道，他在五个不同的时刻对这个星球进行了五次观测得出五组数据。基于此，他在轨道平面内建立了以太阳为原点的空间直角坐标系，现在根据其给出的数据，确定小行星轨道并画出，根据二次曲线理论，计算小行星椭圆轨道的重要参数，包括长半轴短半轴近日点距等，考虑合适的方法计算其近日点坐标，查阅二次曲线不变量的相关知识，尝试给出椭圆变换为最简方程形式的推导过程或证明。

2.模型假设

假设小行星符合开普勒第一定律
假设此天文学家观察准确，数据无异常
假设小行星可以视为质点
假设忽略其他行星对于此小行星的影响
假设其轨道为标准的椭圆形

3.问题分析

由开普勒第一定律我们可以知道，行星的轨道是一个椭圆，所以我们可以将数据带入Ax²+Bxy+Cy²+D+Ey+F=0，首先构成行星的轨道的轨迹方程，并将其画出。然后根据第二问提供条件，加上第一问我们已经得出椭圆方程，旋转平移不会影响椭圆的焦距之类性质，首先要做的是要把椭圆的二次曲线变成椭圆的标准方程，然后我们可以先借助第一问的已知条件去求解第二问里面的问题，借助那些不变的条件去推导那些变化的条件，然后将第二问要求的数据求出。在得出第二问里的数据之后，我们可以利用现在的椭圆方程，以及长短半轴长等数据，带入弧长近似公式把此轨道求出，然后因为我们是以太阳为原点建立的坐标系，所以求近日点远日点坐标其实就是求距离原点最近的点与最远的点，可以在得出图像之后观察或者运用几何知识将其求出，最后一问则是将得出的椭圆方程的矩阵求出，根据二次曲线的不变量得出其最简的方程式。

4.符号说明

x=[4.5596 5.0816 5.5546 5.9636 6.2756]'

y=[0.8145 1.3685 1.9895 2.6925 3.5265]'

X为椭圆方程各个参数的矩阵

A=[x.^2 2*x.*y y.^2 2*x 2*y];

b=-1*ones(5,1);

a为长半轴

b为短半轴

半焦距c

近日点距离h

椭圆周长为L

5.模型建立

%%
%AX=b ==> X=inv(A)*b

%建立坐标矩阵
x=[4.5596 5.0816 5.5546 5.9636 6.2756]';
y=[0.8145 1.3685 1.9895 2.6925 3.5265]';

%确定矩阵参数
A=[x.^2 2*x.*y y.^2 2*x 2*y];
b=-1*ones(5,1);

%根据矩阵求解
X=A\b
a1=X(1);a2=X(2);a3=X(3);a4=X(4);a5=X(5);

%绘图
subplot(2,2,1)
fimplicit(@(x,y)a1*x.^2+2*a2*x.*y+a3*y.^2+2*a4*x+2*a5*y+1,[-2,8])
title('小行星轨道')
xlabel('x轴')
ylabel("y轴")
hold on
plot(x,y,'bo')
plot(0,0,'r*')
hold off

%%
%求C行列式的值
C=[a1 a2;a2 a3];
detC=det(C); 

%求解C的特征值
[C1,C2]=eig(C);

%求解D的行列式值
D=[a1 a2 a4;a2 a3 a5;a4 a5 1];
detD=det(D);

%求椭圆长半轴a的值
A=det(D)./( 0.5502.*det(C));
a=sqrt(A)

%求椭圆短半轴b的值
B=det(D)./(0.1694.*det(C));
b=sqrt(B)

%求椭圆半焦距c的值
c=sqrt(B-A)

%%
%绘制标准椭圆二维图
t=0:0.1:(2*pi+0.1);
x=a*cos(t);
y=b*sin(t);
subplot(2,2,2)
plot(x,y),grid on
title('标准椭圆二维图')
xlabel('x轴')
ylabel("y轴")

%%
%求出椭圆的中心点
xc=(2*a2*2*a5-2*a3*2*a4)/(4*a1*a3-2*2*a2*a2)
yc=(2*a2*2*a4-2*a1*2*a5)/(4*a1*a3-2*2*a2*a2)

%%
%画出直径为长轴的圆和椭圆
subplot(2,2,3)
fimplicit(@(x,y)a1*x.^2+2*a2*x.*y+a3*y.^2+2*a4*x+2*a5*y+1,[-2,8])
hold on
fimplicit(@(x,y)x.^2-2*xc*x+xc^2+y.^2-2*yc*y+yc^2-b^2)
hold off

%%
%计算切点得到近日点和远日点
syms x y;
T=solve(a1*x.^2+2*a2*x.*y+a3*y.^2+2*a4*x+2*a5*y==-1,x.^2-2*xc*x+xc^2+y.^2-2*yc*y+yc^2-b^2==0,x,y,'Real',true);
x=double(T.x)
y=double(T.y)

%%
%求解标准椭圆方程的周长
syms x;
f=sqrt(a^2.*(sin(x)).^2+b^2.*(cos(x)).^2);
L1=int(f,0,pi/2);
L=vpa(4*L1,7)

这段代码主要用于处理椭圆的拟合和分析。具体包括以下步骤：

建立坐标矩阵：定义了 x 和 y 的数据点，并构建了矩阵 A 和向量 b。
求解矩阵方程：通过 X = A\b 求解出椭圆参数。
绘制椭圆：使用参数绘制椭圆，并标出数据点和原点。
计算行列式和特征值：计算矩阵 C 和 D 的行列式和特征值。
计算椭圆参数：求解椭圆的长半轴 (a)、短半轴 (b) 和焦距 (c)。
绘制标准椭圆：绘制标准椭圆的二维图。
求椭圆中心：计算椭圆的中心点坐标。
绘制直径为长轴的圆和椭圆：绘制椭圆及其长轴的圆。
计算近日点和远日点：通过解方程求出椭圆的近日点和远日点。
计算椭圆周长：使用积分计算椭圆的周长。

6.模型求解

下为行星轨道与椭圆轨道及求解中间图

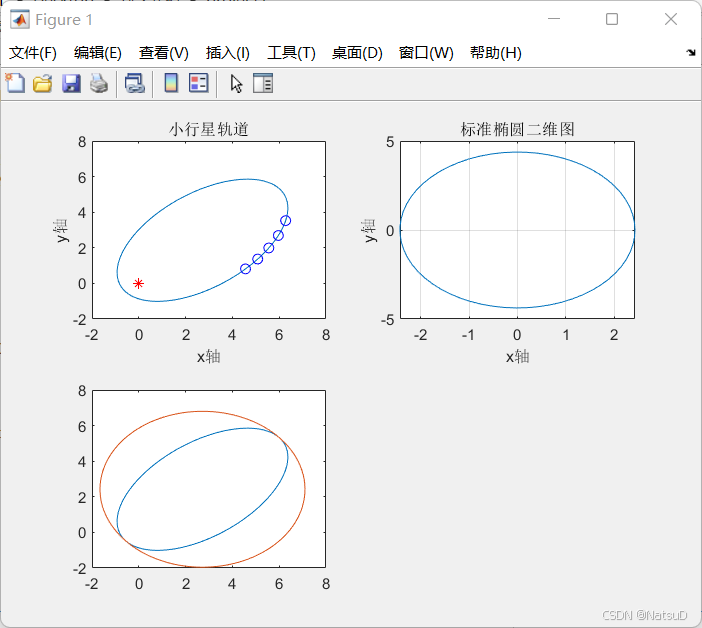
>> project1

X =

   -0.3378

    0.1892

   -0.3818

    0.4609

    0.4104

a =

    2.4300

b =

    4.3793

c =

    3.6433

x =

   -0.5806

   -0.5173

    6.0232

    5.9600

y =

   -0.4534

   -0.5243

    5.3002

    5.3712

L =

21.83255

7.变化展示

根据二次曲线不变量的理论，我们的曲线方程为a1*x.^2+2*a2*x.*y+a3*y.^2+2*a4*x+2*a5*y+1=0（值已在模型中求出），其系数均不为零，设Z=a1*x.^2+2*a2*x.*y+a3*y.^2+2*a4*x+2*a5*y+1，设T为其二次项部分，所以T=a1*x.^2+2*a2*x.*y+a3*y.^2。

所以Z=[x y 1]*D*[x;y;1],T=[x y]*C*[x;y],所以D=[a1 a2 a4;a2 a3 a5;a4 a5 1],C=[a1 a2;a2 a3](此处a1 等值与上文所求值出不一样)，由二次曲线不变量可知，椭圆的最简方程式为

，又因为二次曲线不变量里的定义I3=|D|,I2=|C|,所以我们可以得知，椭圆方程可以如以上化为题目显示的最简方程形式。

8.模型优缺点

模型最终运算结果较为准确，经核验结果可行性极高，图形结果直观简便，符合题目要求及现实情况，此模型由少量简单容易计算的例子推导出普适性可以广泛运用的实例，采用了较为成熟的数学建模，可推广性较高，数据准确丰富翔实，数据直观，把行星轨道的数据和方式以一种数字的方式比较直观的列出，方便检验，可以充分解决问题。但此模型得出结果是在种种假设下以开普勒定律求出的，未考虑其他行星引力等复杂情况，是一种理想下的产物，在现实里的种种复杂情况下实用性并不是太高，只能当作辅助判断来用。