向量是线性代数研究的基本元素。
线性代数的重点在于其推广一个数的研究到一组数的研究。使用 向量(Vector) 能用来更好地描述多维度世界。
从方向的视角立看待向量:表征从一个点出发到另一个点的相应的结果,并不描述得到相应结果的过程差异(如起始点的不同),为了研究方便,我们定义的向量都是从原点开始的(类比数轴,实数的值都是相对数轴上的0的距离的描述)。
零向量 O \color {red} {\small 零向量O} 零向量O :数学上不直接定义什么是零向量,而是由从一个性质:**“对于任意一个向量 u ⃗ \vec u u ,都存在一个向量 O O O,满足: u ⃗ + O = u ⃗ \vec u + O = \vec u u+O=u”**来推导出零向量 O O O的存在。当在一个空间证明出了这个向量的存在,才称这个向量为零向量 O O O。从方向的视角来看待零向量,那么零向量 O O O就是从坐标原点(零向量本身)出发又指向零向量,所以零向量不是一个有向线段,它依然是一个点。因此 零向量是一个特殊的向量,称呼它为一个向量是为了向量系统的统一,但是它本质是没有方向的,它就是一个点,而且就是坐标系的原点。
n n n维向量:在自然科学领域,有时一个单纯数量就可以量化某个物理量,如体积能够直观反映物体占用的空间大小。 但多数情况下,单纯的数量,不能准确表示一个物理量。所以引入向量的概念,来准确地描述一些事物。
如果使用一个5维向量可以对一个房子具像描述为:

一个向量具有两个属性,方向和大小,一个向量大小为模,方向由向量对应的单位向量进行表示。分析时可以提取向量的的单一属性进行分析。
向量的模(module): 含义向量的大小,也就是向量的长度(或称模),向量 u ⃗ 的模 \vec {u}的模 u的模记作 ∥ u ⃗ ∥ \|\vec {u}\| ∥u∥。
-
二维平面的向量的模的计算: ∥ u ⃗ = O P ⃗ = ( x , y ) ∥ = x 2 + y 2 \|\vec {u} =\vec {OP}= (x,y)\|=\sqrt {x^2 + y^2} ∥u=OP=(x,y)∥=x2+y2
-
三维空间的向量的模的计算: ∥ u ⃗ = O P ⃗ = ( x , y , z ) ∥ = x 2 + y 2 + z 2 \|\vec {u} =\vec {OP}= (x,y,z)\|=\sqrt {x^2 + y^2 + z^2} ∥u=OP=(x,y,z)∥=x2+y2+z2
-
推广到 n n n维空间的向量的模的计算: ∥ u ⃗ ∥ = ( u 1 , u 2 , . . . , u n ) T = u 1 2 + u 2 2 + . . . + u n 2 \|\vec {u} \|= (u_1,u_2,...,u_n)^T = \sqrt {u^2_1 + u^2_2 + ... + u^2_n} ∥u∥=(u1,u2,...,un)T=u12+u22+...+un2
单位向量(unit vector): 仅用以表示向量方向的向量。单位向量的模为$|\hat {u}| = 1
.
其中,根据
. 其中,根据
.其中,根据\vec {u}
求出
求出
求出\hat {u}$的过程称为:归一化,规范化(normalize)。
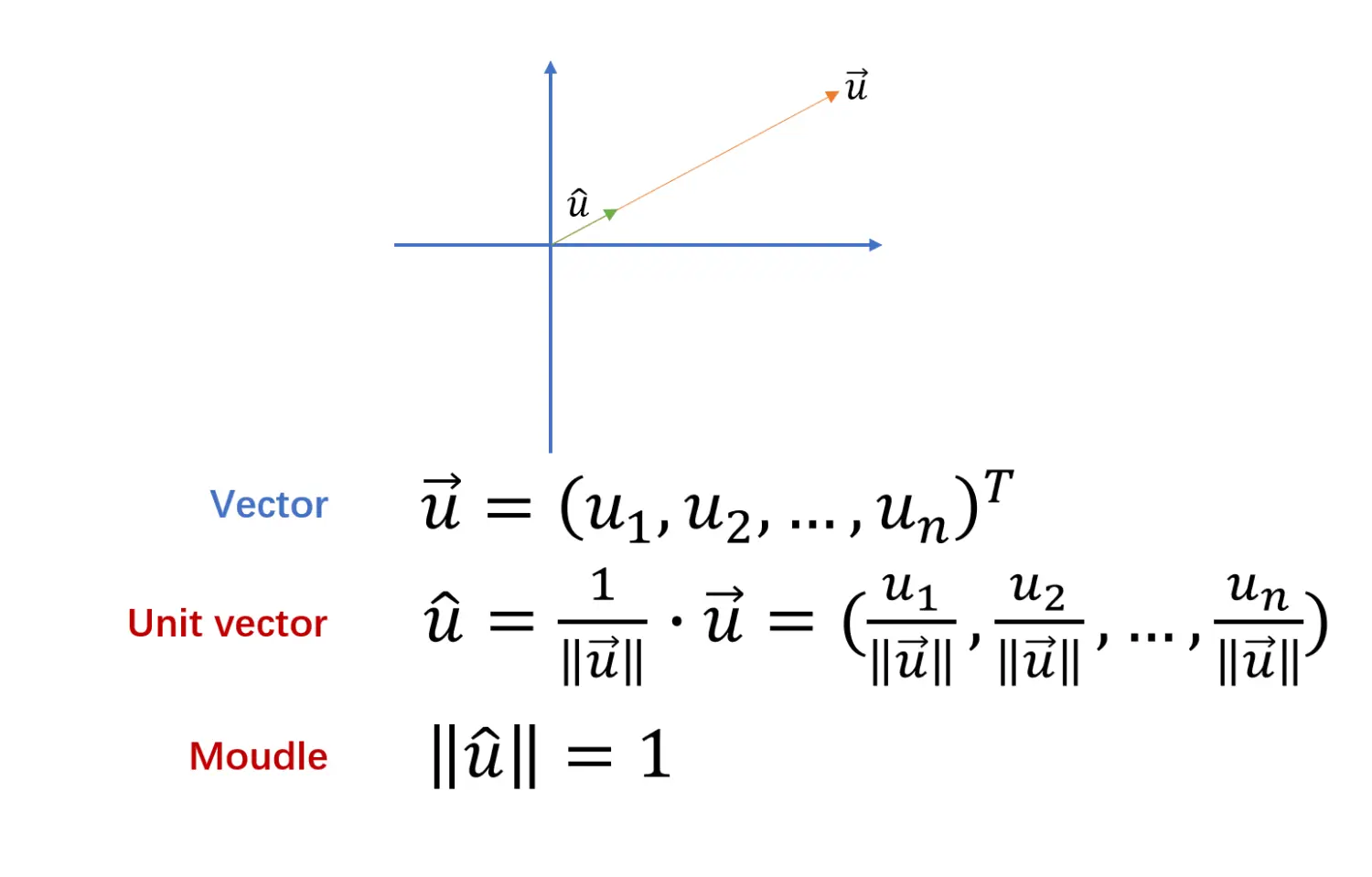


























 1447
1447

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










