【论文阅读】Cancellable iris template generation based on Indexing-First-One hashing

最新推荐文章于 2024-11-02 22:07:44 发布

2^silence

最新推荐文章于 2024-11-02 22:07:44 发布

阅读量472

点赞数

文章标签：论文阅读算法图像处理

本文链接：https://blog.csdn.net/Ning_yuan/article/details/126909785

版权

1. 介绍

简介生物特征识别的由来。

虹膜识别被认为是具有很高的可靠性由于它的可辨性和可靠性，一生中不变，不受环境和遗传因素的影响。Daugman是第一个发明实用的自动虹膜识别系统的人，是最受欢迎的虹膜表示法的发明者。已经证实虹膜模式的熵比其他生物特征高，这意味着虹膜更不容易发生错误匹配。

可撤销的生物特征方法在注册和识别的时候通过应用某些转换函数使生物特征变形，设计出良好的可撤销生物方案要满足以下四个标准：

1.不可链接性

2.可撤销性

3.不可逆性：从受保护的模板和/或辅助数据导出其原始对应物在计算上应该是不可行的；因此，它防止了被泄露的生物测定数据的滥用，并增强了系统的安全性。

4.性能：大致保持和原始的不变

1.1 相关工作

1.1.1 Salting approach iris template

在biometric salting，独立的辅助数据例如用户专用的密码和令牌结合生物数据生成变形的生物模板。该方法的一个例子S-IrisCode encoding，虹膜Gabor-feature向量 $\omega \in C^{n}$ 通过与归一化的虹膜图像卷积the 1-D log-Gabor filter产生，然后重塑一个n维的特征向量，表示为w通过对用户特定的标准标准正交随机向量（其中m ≤ n）的迭代内积被映射到一个低维的特征空间。执行量化的过程计算，从计算出 $s_{i}$ ， $s_{i}$ = 0 当 $\alpha$ ≤ 0 ； $s_{i}$ = 1 当 $\alpha$ > 0；一旦被泄露，新的生物特征模板根据给出的来自用户特定令牌的新的随机向量集合再生。

为了提高精度性能，利用噪声掩码， $s_{iN}$ = 0当α < − σandα > σ，噪声掩模作为控制比特，通过剔除弱内积来确定 $s_{i}$ 比特的有效性，从而提高了汉明距离匹配的正确性。

Zuo et al.提出了一个salting method应用在实值虹膜模式或者二值虹膜模式，叫做GREY-SALT and BINSALT。在GREY-SALT中，在虹膜图案上添加或乘以人工图案。对于BIN- SALT，对IrisCode和随机二值密钥图案应用异或操作，For both GREY-SALT and BIN- SALT,虹膜信息被辅助数据掩盖。从而通过替换辅助数据实现可取消的虹膜模板刷新。然而，如果不进行预对齐处理，精度性能可能会显著下降。

除了利用整个虹膜图像，Pillai et al.使用分区的随机随机映射生成可撤销虹膜模板，他们指出，通过用户特定的随机矩阵直接投影虹膜图像，可能不可避免地会由于睫毛、镜面反射和眼皮等噪声以及虹膜图像不同区域的质量不均匀而导致性能下降。因此，含有噪声的良好虹膜区域的线性变换破坏了数据。在他们的工作中，将虹膜分割成几个扇区，然后通过用户特定的随机高斯矩阵将每个扇区的Gabor特征投影到较低维空间。最后，通过将不同部门的预测产出连接起来，生成了可取消模板。在如传统虹膜识别系统[2，3，19]中的特征编码过程之后，可以生成可取消的虹膜编码。他们的工作在压缩原始模板的同时保持了精度性能。可以通过使用不同的随机投影矩阵来生成新的模板。

然而，孔令辉等人。[20]和Lacharme等人。[21]结果表明，如果将相同的随机矩阵应用于不同的用户，精度性能将显著降低，并且当特定于用户的随机矩阵被泄露给攻击者时，可取消模板极有可能被反转(被盗令牌情况)。这意味着，一般而言，当且仅当辅助数据保密时，生物测定盐化是可行的。

1.1.2 虹膜模板不可逆的转换方法

在不可逆变换中，使用单向变换函数对虹膜模板进行变换，其中变换后的虹膜模板是不可逆的，并且可以安全地存储在数据库中。

Zuo等人。[16]提出了两种虹膜模板的不可逆变换方法，即灰度组合和BIN组合（GREY-COMBO and BIN- COMBO）。在灰度组合中，他们通过随机偏移量(随机键)以行的方式移动虹膜图像，然后对两个随机选择的行进行运算(加法或乘法)。在BIN_COMBO中，对IrisCode执行了相同的过程，但使用了XOR或XNOR运算。这样，原始虹膜数据由于两个随机选择的行特征之间的加法/乘法运算而失真，从而满足不可逆性准则。在GREAY-COMBO和BIN_COMBO中，无论旋转与否，虹膜模板的移位行总是在相同的方向上，因此它是无配准的，这意味着匹配不需要对齐。然而，当使用质量较差的虹膜图像时，第一种方法的性能会下降。然而，由于他们使用特定于用户的密钥，这就暴露了在加盐方法中令牌被盗的风险。

Hämmerle-Uhl等人。[15]采用块重映射法进行不可逆变换。归一化后的虹膜图像首先被分割成多个图像块，然后用密钥随机置换。采用图像块重映射技术生成可取消模板。在该过程中，初始化了与源虹膜图像大小相同的目标图像。然后，将源图像中的不同图像块映射到目标图像。允许对同一图像块进行多次重新映射。有损重映射过程阻止了原始虹膜图像的重建，并且满足不可逆性准则。尽管该方案没有危及精度性能，Jenisch等人还是这样认为。[24]然而，证明了60%的原始虹膜图像可以从被盗的模板中恢复。

Ouda等人。[25，26]提出了一种无令牌的IrisCode模板保护方案，即生物编码。他们首先从每个用户的几个IrisCodes中确定“一致性位”。一致性比特是指在收集的几个样本中具有较低翻转概率的比特。一致性位 $C\in \begin{Bmatrix} 1,0 \end{Bmatrix}^{n}$ ，其中n表示一致位向量的长度，其中n∈[332,3737]。此外，创建并存储了记录C中一致性位的位置的位置向量 $P\in \begin{Bmatrix} 0,1 \end{Bmatrix}^{n}$ 。最后，将C分割成m个二进制码字，并将每个码字编码成随机生成的二进制序列 $S\in \left \{ 1,0 \right \}^{l}$ ，其中l=n/m以呈现BioCode， $B\in \left \{ 1,0 \right \}^{l}$ 。例如，当m=5时，如果被寻址的码字是 $10011_{m}$ (十进制19)，则对应的Biocode比特将根据S中的第19比特值输出‘0’或‘1’。在此时刻，相同的码字将输出相同的比特，从而产生有损的多对一映射，因此，满足不可逆性。为了进一步保护方案免受相关攻击，在生物编码发生之前，对第二个随机序列进行异或或与IrisCode进行置换。他们的作品也显示出相对于未受保护的同行的准确性和性能保持性。然而，Lacharme[27]指出，Biocode的不可逆性是无效的。当用于生成随机序列的布尔函数被暴露时，恢复的可能性很高。

Rathgeb et al.提出用布隆过滤器，Bloom Filter的精确度性能与原始同类相当，然而，Herma等人。[29]指出可以以2^25的低复杂度恢复模板。他们还提出了一种攻击，其中从同一IrisCode生成的两个Bloom过滤器b1和b2可以以大约96%的高概率被识别。Bringer等人。[30]还指出，由于密钥空间较小，旨在保持准确性性能，因此不可链接性攻击的可能性很高。Gomez-Barrero等人最近所做的工作。[31]展示了如何在基于Bloom Filter的模板保护方案中防止交叉匹配攻击。

Dwivedi等人。[32]提出了一种基于查找表的可取消虹膜模板。他们首先通过将IrisCode的不同样本相对于同一用户生成的参考模板左右移动来生成旋转不变虹膜模板。然后，通过添加旋转不变码的每一行来形成单行向量 $C\in \left \{ 1,0 \right \}^{1\times N}$ ，其中N表示行向量的长度。然后，将C进一步划分为l个二进制码字，每个码字由m比特组成，从而l=C/m。每个码字表示的十进制值表示为 $d=\left \{ d_{i}\in \left [ 1,2^{m}-1 \right ]|i=1,...,l \right \}$ 被记录下来。随机生成的查找表 $M\in \left \{ 1,0 \right \}^{R\times m}$ 和 $R\geq 2^{m}-1$ 。通过查找映射，对d进行编码，得到可取消的模板。然而，由于查找表应该与可取消模板一起存储，因此在泄露了参数m的情况下，可以容易地恢复IrisCode。

1.2 激励和贡献

基于相似项检测或聚类中常用的最小散列的概念，提出了一种新的基于不可逆变换的可取消虹膜方案，称为索引优先散列(IFO)散列。本质上，IFO散列码是多个随机标记化置换的IrisCode的比特‘1’的第一次出现的索引的集合。该过程具有诸如IrisCode的隐式排序等优点，而不是使用显式比特信息来生成IFO哈希码，这有利于防止反转攻击。此外，我们在Min-Hash算法的基础上引入了两种新机制，即P阶Hadamard乘积和模门限函数(P-order Hadamard product and modulo threshold function)来提升隐私保护。

作为我们在会议[36]上发表的工作的扩展，本文包含了广泛和多样化的实验以及关于不同参数配置的分析。我们还根据几种艺术水平对我们的作品进行了基准测试。更重要的是，进行了几项严格的安全和隐私分析，这在会议版本中是没有的。分析方法包括单哈希攻击、多哈希攻击、记录重数攻击和前置图像攻击。我们认为该方案对上述攻击具有较好的抵抗能力。我们还通过实验证明了IFO散列同时满足可撤销和多样性要求。

2 准备工作

2.1. Min-hashing

可以通过以更大的散列代码存储为代价来增加m（随机排序函数的个数）来最小化误差ε。

2.2 IrisCode 生成

本文中的IrisCode生成采用了文献[28]中的内容。首先应用加权自适应Hough变换检测虹膜区域。然后使用两阶段分割过程来分割虹膜和瞳孔边界[38]。经过归一化处理，将虹膜区域展开为大小为64×512的固定维数组，即橡皮片模型[2]。只保留上面50行以形成大小为50×512像素的虹膜纹理。然后对每五行的像素进行平均，以产生新的一维向量。每个向量用一维log Gabor滤波器卷积，生成10×512的复杂虹膜Gabor特征。最后将虹膜Gabor特征的每个复数值相位化为2比特，生成虹膜编码 $X\in \left \{ 0,1 \right \}^{n1\times n2}$ ，其中n1=20，n2=512，总个数为10240比特。有关IrisCode生成过程的更多详细信息，请参阅[39]。

3. 方法论

3.1. Indexing-First-One (IFO) hashing

IFO散列利用独立的散列函数 $h_{1},...,h_{m}$ 其中每个独立散列函数以列方式从P个标记化置换的IrisCode，X中导出。

m和P均可使用范围[1，∞]进行设置。推导IFO散列函数的过程，描述如下：

1.随机置换：生成包含P个随机生成的置换向量的置换集合θ。置换输入IrisCode X按列生成 $X{}'=\left \{ X{}'_{l}|l=1,...,P \right \}$

2.哈达玛代码生成：生成第p个顺序的Hadamard乘积码 $X^{P}$ ，方法是将所有的X相乘，即 $X{}'s$ , $X^{P}=\prod_{l=1}^{p}\left ( X{}'_{l} \right )$ 。为了防止IrisCode恢复，在此过程中会丢失大量的二进制信息。排列过程和Hadamard乘积也使某些“脆弱”位[40]被排除在外。

3. Construct the K-window：对于产品代码 $X^{P}$ 中的每一行，选择前K个元素，其中 $1\leq K\leq n_{2}$ 。这一步再次丢弃了K窗口之外的二进制信息。

4.在所选择的前K个元素中，记录索引值，表示为对应于第一个出现位‘1’的 $C_{X}$ 。

5.模阈值：通过安全阈值 $\tau$ , $1\leq \tau < K$ 施加模阈值函数来减轻X的泄漏。也就是说，对于每个 $C_{X}\geq K-\tau$ ，计算 $C{}'_{X}=C_{X} mod \left ( K-\tau \right )$ 。施加的模阈值导致了输出 $C_{X}$ 的多对一映射，从而加强了不可逆性。

6.用不同的排列集合 $\theta _{\left ( i,l \right )}$ 重复步骤1-5，其中 $i\in \left [ 1,m \right ]$ ， $l\in [1,P]$ 以形成 $n_{1}\times m$ 个IFO散列码， $C{}'_{X}\in \left \{ 0,K-\tau -1 \right \}$ ,其中 $C{}'_{X}=\left \{ Z^{n_{1}} i=1,...,m\right \}$ 。当 $m< n_{2}$ 时，它导致与原始输入iriscode $X\in \left \{ 0,1 \right \}^{n_{1}\times n_{2}}$ 相比，生成的IFO散列码的维度降低。从步骤1到步骤5的每一轮涉及 $i\in \left [ 1,m \right ]$ 的独立散列函数 $h_{i}$ 。

3.2 匹配

IFO散列码的匹配是一个两步过程，包括预对齐步骤和相似性匹配。

3.2.1 预对齐

有头部倾斜的问题。

通过将查询IrisCode Y向左和向右移位±16比特来执行预对齐。然后，将IFO散列与原始未移位的IrisCode一起应用于每个移位的IrisCode，从而产生33个移位的查询实例。将在登记的散列代码和每个查询实例之间执行匹配，并且只记录最高分数。

3.2.2 与Jacaard相似性的关系

其中1）、2）、3）可以确定是否相等，但是4）不能确定

注意：如果P=1，则IFO散列(没有模阈值)减少到X和Y的最小散列。对于P>1， $X_{P}\left ( Y_{P} \right )$ 包含较少的‘1’(由于比特乘法效应)，当K窗口内包含较少的比特‘1’时，情况(1)的出现概率降低，而情况(2)和情况(3)的发生概率增加。在这种情况下，案例(1)-(3)的概率表明Jacaard相似性的降级。

其中，p∈[0，1]是P≥1的原始Jacaard测量的缩小系数。

3.2.3 相似性度量

为了计算两个散列码相同的概率，可以匹配登记的和查询的散列码，并计算 $C{}'_{X\left ( j,i \right )}=C{}'_{Y\left ( j,i \right )}$ 的概率。当K很小的时候，’1‘有可能不存在。在这种情况下 $C{}'_{X\left ( j,i \right )}=0$ 。

在实际应用中，为了简单起见，我们可以将匹配算法表示在Hamming域上。

为了排除匹配过程中的病态，我们首先初始化一个二进制零矩阵 $B_{X}\left ( B_{Y} \right )\in \left \{ 0,1 \right \}^{n_{1}\times m}$ ，并且仅当 $C{}'_{X\left ( j,i \right )}\left ( C{}'_{Y\left ( j,i \right )} \right )\neq 0$ 时才用‘1’填充。另一方面，我们引入了另一个二进制矩阵 $Q_{XY}$ ，它也是以零初始化的。然后，给定 $C{}'_{X}$ 和 $C{}'_{Y}$ ，如果对于 $j\in \left [ 1,n_{1} \right ]$ ，and $i\in \left [ 1,m \right ]$ ，如果 $C{}'_{X\left ( j,i \right )}= C{}'_{Y\left ( j,i \right )}$ ，则将 $Q_{X\left ( j,i \right )Y\left ( j,i \right )}$ 设为‘1’。最后， $C{}'_{X}$ 和 $C{}'_{Y}$ 的相似度可以计算如下：

实际上，在IrisCode中出现比特0或1的概率是伯努利试验[2，3]。这表明，对于Hadamard积中选定的P，缩减因子p可以是常数。

4 实验和分析

使用CASIA database v3-interval评估精度性能，来自396个不同类别(眼睛)的2639张虹膜图像，只有左眼。为了标准化匹配，从所有的左眼图像中，我们只选择了包含至少7个虹膜样本的子集，总共得到124个类别，因此124*7=868个虹膜图像。对于类内比较，将每个虹膜模板与从相同类的其他虹膜样本生成的模板进行匹配，从而产生总共2604（=124*（6+5+4+3+2+1））个真实的比较。对于类间比较，将每个模板与从不同类的不同虹膜样本生成的所有其他模板进行匹配，总共产生373674（=7*7*（123+122+121+...+2+1））个冒名顶替者比较。

4.1 性能评估

不同参数K、m、p和 $\tau$ 对EER的影响。

原始虹膜编码基于汉明码距离位移±16bits的结果：

4.1.1 参数m的影响

研究了散列函数个数m与验证性能的关系。当m=200时，EER接近IrisCode的性能。K越小性能越差，这受到由于在IFO散列期间定位第一个二进制位‘1’的失败情况的影响。

4.1.2 参数K和P的影响

P越大EER越大，这是由于Hadamard乘积的直接结果导致K窗口中比特“1”的出现次数较少，这相当于按位AND运算。

4.1.3 参数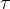 $\tau$ 的影响

$\tau$ 用来衡量不可逆性。当 $\tau$ >0.9K时才有影响，这是因为较大的 $\tau$ 缩小了 $C{}'_{X_{i}}$ 的有效范围，这也意味着信息丢失。然而，这一特性是有利的，因为损失促进了IFO散列的不可逆能力，尽管较大的 $\tau$ 降低了性能。只要 $\tau$ <0.9K，这个问题确实是可控的。

4.1.4 与最先进水平的比较

研究样本个数对实验结果的影响

4.2 不可逆分析

在我们的分析中，假设攻击者获得了关于IFO散列算法、参数(K、P、 $\tau$ 和m)、被盗的散列码和置换令牌的所有信息。在这种情况下，攻击者可以彻底了解 K-window bits和 IrisCode之间的关系。

单哈希攻击、多哈希攻击、记录重数攻击(ARM)和前映像攻击。

在这些分析中，我们采用 $\tau$ ≥K/2，这是强保护的必要条件。

4.2.1 单哈希攻击

讨论从单个IFO哈希码条目 $C{}'_{X_{i}}$ 恢复IrisCode的可能性.

SHA确实是IFO暴力攻击的特例。与应用于整个模板的传统暴力攻击不同，SHA仅针对散列码 $C{}'_{X_{i}}$ 的单个条目。

为了测量K窗口比特重构的SHA复杂性，需要首先估计可能的模映射的数目r。所以 $K-\tau =\frac{K}{r}$ ， $r\left ( 1-\frac{\tau }{K} \right )=1$ 。这意味着对于 $\tau$ <0.9K， $C{}'_{Xi}\in \left [ 1,K-\tau -1 \right ]$ 允许r∈[2，9]可能的映射。这允许我们估计最小猜测次数，即 $n_{1}r^{m}$ 以从 $C{}'_{X_{i}}$ 完全恢复 $C_{Xi}$ 。

当K窗口比特为1时，攻击者可以基于φ中给出的索引来推断对应的P比特也是1。这是因为K窗口比特的唯一方式是当给定φ的所有P个比特都是1时，K窗口比特是1。另一方面，当K窗口比特是‘0’时，由于‘0’和‘1’的P个随机置换的阿达玛乘积，它允许每个K窗口比特的 $2^{P}-1$ 个组合为‘0’。例如，当P=2时，存在 $2^{2}$ -1=3种方式使两个二进制位的乘积为‘0’，如(0，0)、(0，1)和(1，0)。在这种情况下，对手将不得不搜索所有可能的组合，这与K窗位为‘1’的情况相比更加困难。图7说明了K=3和P=3的令牌被盗案例中的IrisCode恢复。

随着简并度的提高，恢复的二进制位‘1’的数量将减少。对于上限，我们总是假设φd由P个不同的索引值组成，其中我们表示为 $\left | \varphi {_{d}}^{*} \right |=P$ ， $\varphi {_{d}}^{*}$ 代表在 $\varphi _{d}$ 中的不同元素。

由于存在不同数量的‘1’，因此很难推断出n的绝对值。可以作出如下假设：对于每个独立的IrisCode，所有比特值的可能性相等。根据该假设，每个随机置换的IrisCode可以被认为是一个新的独立实例，因此在置换的IrisCode的P个Hadamard乘积之后的K窗口中的‘1’的数目是： $n\approx K\left ( \frac{1}{2} \right )^{p}$

估计得到最小的猜测数目是 $n_{1}r\cdot 2^{n_{2}}$ ，这意味着对手将必须尝试至少 $2^{512}$ 次才能恢复IrisCode。

步骤如下：

4.2.2 多哈希攻击

分析了一种强不可逆分析下的非均匀攻击。与仅基于单个 $C{}'_{Xi}$ 的SHA不同，对手可以在 $i\in \left [ 1,m \right ]$ 的散列代码中使用多个 $C{}'_{Xi}$ 发起攻击。

为了计算MHA的复杂度，我们遵循前面的命题，使得IrisCode中的“0”和“1”的个数可能相等，因此如果大约一半的比特“1”，即，则可以完全恢复IrisCode。n2/2，在每一行中，IrisCode都是对手所知道的.这是可能的，方法是首先生成与IrisCode大小相同的稀疏码，并简单地猜测剩余的未知位都是‘0’或‘1’。完全重新生成整个原始IrisCode所需的Cxi值的数量可以通过简单地 $\frac{n_{2}}{2P}$ 计算，复杂性是 $n_{1}r^{\frac{n_{2}}{2P}}$ ，让 $m< \frac{n_{2}}{2P}$ 可以防止多哈希攻击。

4.2.3 记录重数攻击

ARM指的是隐私攻击，其利用具有和不具有关联信息的多个受保护模板，即助手数据、参数等来重建原始生物测定模板。对于ARM攻击，我们需要考虑到对手可以通过多个泄露的IFO哈希码来学习。

4.2.4 前映像攻击

与以前的攻击不同，通过阻止对手恢复IrisCode来保护隐私。PIA旨在通过利用受保护生物识别模板中原始生物识别数据(也称为前像)的接近程度来非法访问生物识别系统，攻击复杂性较低[12]。

为了访问生物测定系统，生物测定输入不必与登记的模板相同。例如，Jerish等人。[24]成功启动了PIA，其中仅利用了60%的IrisCode信息。此外，Bringer et al.。[30]还能够在块宽度为16和32的基于Bloom Filter的受保护虹膜模板[28]上启动PIA。Nagar等人[33]演示了从基于BioHash的受保护生物特征模板学习前图像的技术。

该复杂性是基于50%的IrisCode信息的先验知识来计算的。我们假设攻击者只有在成功恢复至少2(0.25)×100%=50%的IrisCode时才能访问系统，其中t=0。25，这在现实中是合理的。与ARM和MHA相比，PIA的攻击复杂度大大降低到 $n_{1}r\frac{n_{2}}{4P}$ 。

4.3 可撤销性分析

将第一个散列码与其余99个散列码进行匹配，以计算伪冒名者分数，产生99 × 7 × 124 = 85932个伪冒名者分数。注意，冒名顶替者和伪冒名顶替者匹配是在不移位的情况下进行的，以减少计算负担。

可以观察到在冒名顶替者和伪冒名顶替者分布之间发生了很大程度的重叠。事实上，新的散列码充当了旧散列码的“冒名顶替者”，因为它们是不相关的。这验证了IFO散列满足可撤销要求，即新的散列代码能够用不同的置换令牌替换旧的代码。

4.4 不可链接性分析

可以合理地推断，如果所有置换的IrisCodes都是独立的，那么 $C{}'_{Xi}$ 也将是独立的。因此，由m个散列条目组成的IFO散列码将是独立的，然后满足不可链接性。

在此，我们遵循[2，3]中所报道的道格曼的独立测试来对置换的IrisCode进行不可链接性测试。道格曼报告说，由于IrisCode的相位编码概率相等，两个不同的IrisCodes是不相关的，理想情况下它们的预期汉明距离为0.5。道格曼执行了大约910万对IrisCodes的配对，并生成了均值=0.499，标准差=0.0317的类似二项分布曲线。对于两个不同的IrisCodes来说，不同的IrisCodes不可能不超过其相位代码的1/3。如果IrisCode中的所有位都是独立的，则分布曲线将非常尖锐(较小的标准偏差)。从实验中我们可以推断，置换后的IrisCode是独立的，并且满足不可链接性。

此外，仅仅对置换后的IrisCode进行独立性测试可能是不够的，我们还进行了另一种基于 pseudo-genuine score的实验来评估IFO哈希码的不可链接性。伪真分数是指试验者的不同IrisCode使用不同的置换令牌生成的IFO哈希码的匹配分数。与真匹配相同， the pseudo-genuine scores由2667个匹配得分组成。当the pseudo-imposter and pseudo-genuine分布重叠，这表明我们不能区分从同一主题生成的IFO哈希码或从其他主题生成的IFO哈希码。区分IFO散列码的困难导致了不可链接性。

5 总结

对于每个散列值，IFO散列码大小可以估计为 $\log {_{2}}^{K}$ 比特。使用小K，可以节省更多的存储空间，但安全回报较低。