EM算法

EM算法（Expectation-maximization algorithm），即最大期望算法，在统计中被用于寻找，依赖于不可观察的隐性变量的概率模型中，参数的最大似然估计。

在统计计算中，最大期望（EM）算法是在概率模型中寻找参数最大似然估计或者最大后验估计的算法，其中概率模型依赖于无法观测的隐藏变量（Latent Variable）。最大期望经常用在机器学习和计算机视觉的数据聚类（Data Clustering）领域。最大期望算法经过两个步骤交替进行计算，第一步是计算期望（E），利用对隐藏变量的现有估计值，计算其最大似然估计值；第二步是最大化（M），最大化在E步上求得的最大似然值(Maximum likelihood estimation)来计算参数的值。M步上找到的参数估计值被用于下一个E步计算中，这个过程不断交替进行。 —— [ 维基百科 ]

在介绍EM算法之前，先引入极大似然估计

极大似然估计

假如我们遇见了以下的问题：调查男生的身高分布，随机测量100个男生的身高，则得到了样本量为100的样本。假设男生身高服从正态分布，即$N(\mu,\sigma)$，接下来要做的就是估计$\theta=(\mu,\sigma)^T$，此时可用极大似然估计。

假设n个独立同分布样本$\{x_1,…,x_n\}$，密度函数为$p(x;\theta)$。于是联合密度函数

$$p(x_1,…,x_n;\theta)=\prod_{i=1}^{n}{p(x_i;\theta)}$$
在样本 $x_i$已知，而参数 $\theta$未知的情况下，上式可看为 $\theta$的函数，即
$$L(\theta)=\prod_{i=1}^{n}{p(x_i;\theta)}$$
称 $L(\theta)$为 $\theta$的似然函数。
称 $$\hat{\theta}=\arg\max⁡ L(\theta)$$ 为 $\theta$的极大似然估计。

若似然函数$L(\theta)$连续可微，可以通过求$L(\theta)$的极大值来求解，即令似然函数的导数为0。
由于$L(\theta)$是“连乘”的式子，求导会很复杂。可以通过$\ln⁡(x)$转化成“连加”形式。

$$l(\theta)=\ln⁡ L(\theta)=\sum_{i=1}^{n}{\ln p(x_i;\theta)}$$
由于 $\ln⁡(x)$是严格单调递增函数，所以 $l(\theta)$与 $L(\theta)$在同一点达到最大值。由此，求解问题转化成了求解似然方程
$$\dfrac{d\ln L(\theta)}{d\theta}=0$$

注：

• 有些情况的极大似然估计不能通过上述方式求得，例如均匀分布。
• 有些情况的极大似然估计不存在。

EM算法

问题

如果上述问题变为不局限于男生，是调查学生的身高分布，随机抽样了100个学生的身高，而这100个样本有男生也有女生，并且没有标记男女。由常识可知，男生的身高分布和女生身高分布是不同的。此时样本有了类别之分，某个样本不知道是服从男生的分布还是女生的分布。就不能直接用极大似然估计了。

对于这个问题，记$z=1$为男性，$z=2$为女性，男身高分布为$N(\mu_1,\sigma_1)$，女身高分布为$N(\mu_2,\sigma_2)$，即$(x│z=j)\sim N(\mu_j,\sigma_j)$。
于是

$$p(x,z;\sigma)=p(x|z;\sigma)p(z;\theta)$$
其中 $p(x|z=j;\theta)$为 $N(\mu_j,\sigma_j)$的密度函数， $\theta=(\mu_1,\sigma_1,\mu_2,\sigma_2,\phi)$， $\phi=p(z=1)$。

分析

样本集是$\{x_1,…,x_n\}$，每个样本$x_i$对应的类别$z_i$是未知的，即隐含变量。例如上述问题中$\{x_1,x_2,x_3\}=\{171,158,175\}$，虽未知但实际对应的$\{z_1,z_2,z_3\}=\{1,2,1\}$。

参数$\theta$已知时，$z_i$的分布也已知，即$p(z_i;\theta)$，若此时给定$z_i$的取值，$x_i$的分布已知，即$p(x_i│z_i;\theta)$，由此$p(x_i,z_i;\theta)$和$p(z_i│x_i;\theta)$均可计算得到。

推导

对每个$x_i$，希望找到$z_i$，使得$p(x_i,z_i;\theta)$最大。
似然函数

$$\begin{align*} l(\theta)&=\sum_{i}{\ln⁡ p(x_i;\theta)} \\ &=\sum_{i}{\ln⁡\sum_{z_i}{p(x_i,z_i;\theta)}} \end{align*}$$
因为有取值未知的隐变量 $z$存在，使得求解$\theta$一般比较困难。若z能确定，求解就容易了。

考虑每一个样本$x_i$，让$Q_i$表示该样例隐含变量$z_i$的某种分布，$Q_i$满足的条件是$\sum_{z_i}{Q_i(z_i)}=1$，$Q_i(z_i)\geq0$。（如果$z$是连续的，那么$Q_i$是概率密度函数，求和符号需要换成积分符号）

将似然函数可以如下演化

$$\begin{align*} l(\theta)=\sum_{i}{\ln p(x_i;\theta)}&=\sum_{i}{\ln\sum_{z_i}{p(x_i,z_i;\theta)}}\\ &=\sum_{i}{\ln⁡\sum_{z_i}{Q_i(z_i)\dfrac{p(x_i,z_i;\theta)}{Q_i(z_i)}}}\\ &\geq\sum_{i}{\sum_{z_i}{Q_i(z_i)\ln\dfrac{p(x_i,z_i;\theta)}{Q_i(z_i)}}} \end{align*}$$
上述不等号成立是利用了Jensen不等式。

知识补充（Jensen不等式）

如果$f$是凸函数，$X$是随机变量，那么

$$E[f(X)]\geq f(EX)$$
特别地，如果 $f$是严格凸函数，那么$E[f(X)]=f(EX)$当且仅当 $p(X=EX)=1$，即 $X$是常量。

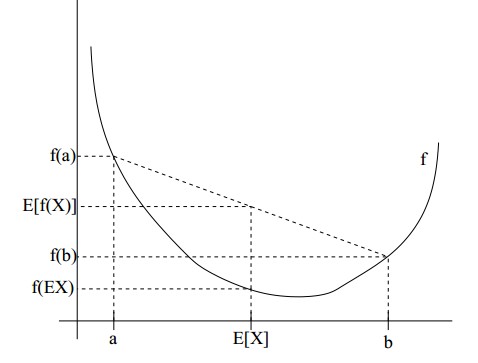
图中，实线$f$是凸函数， $X$是随机变量，有0.5的概率是$a$，有0.5的概率是 $b$。$X$的期望值就是 $a$和$b$的中值了，图中可以看到 $E[f(X)]\geq f(EX)$成立。

Jensen不等式应用于凹函数时，不等号方向反向，也就是

$$E[f(X)]\leq f(EX)$$

下面证明如下不等式

$$\sum_{i}{\ln⁡\sum_{z_i}{Q_i(z_i)\dfrac{p(x_i,z_i;\theta)}{Q_i(z_i)}}}\geq\sum_{i}{\sum_{z_i}{Q_i(z_i)\ln\dfrac{p(x_i,z_i;\theta)}{Q_i(z_i)}}}$$

证明：
令$f(t)=\ln⁡ t$，则$f''(t)=\dfrac{−1}{x^2}<0$，即$f(t)$是凹函数，有

$$E[f(X)]\leq f(EX)$$
令 $Y=g(z_i)=\dfrac{p(x_i,z_i;\theta)}{Q_i(z_i)}$，则
$$\begin{align*} &\ln\sum_{z_i}{Q_i(z_i)\dfrac{p(x_i,z_i;\theta)}{Q_i(z_i)}}\\ =&f\left[\sum_{z_i}{Q_i(z_i)g(z_i)}\right]\\ =&f(EY)≥E[f(Y)]\\ =&\sum_{z_i}{Q_i(z_i)f[g(z_i)]}\\ =&\sum_{z_i}{Q_i(z_i)\ln⁡\dfrac{p(x_i,z_i;\theta)}{Q_i(z_i)}} \end{align*}$$
不等式成立，当且仅当 $\dfrac{p(x_i,z_i;\theta)}{Q_i(z_i)}=c$时等号成立。

上述过程可以看作是对$l(\theta)$求了下界$J(Q_i,\theta)=\sum_{i}{\sum_{z_i}{Q_i(z_i)\ln⁡\dfrac{p(x_i,z_i;\theta)}{Q_i(z_i)}}}$。
假设$\theta$已经给定，那么$J(Q_i,\theta)$的值就决定于$Q_i$了。我们可以通过调整$Q_i$使下界不断上升，以逼近$l(\theta)$的真实值，那么什么时候算是调整好了呢？当不等式变成等式时，说明我们调整后的$J(Q_i,\theta)$能够等价于$l(\theta)$了。
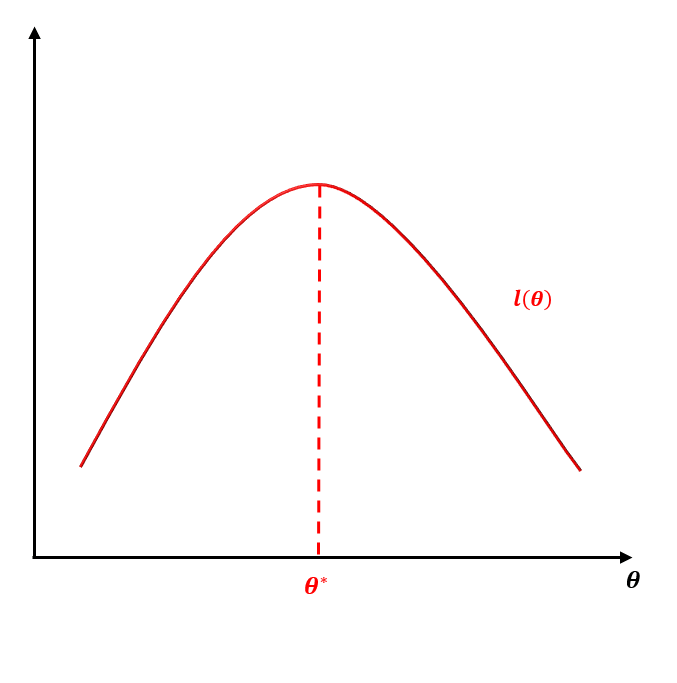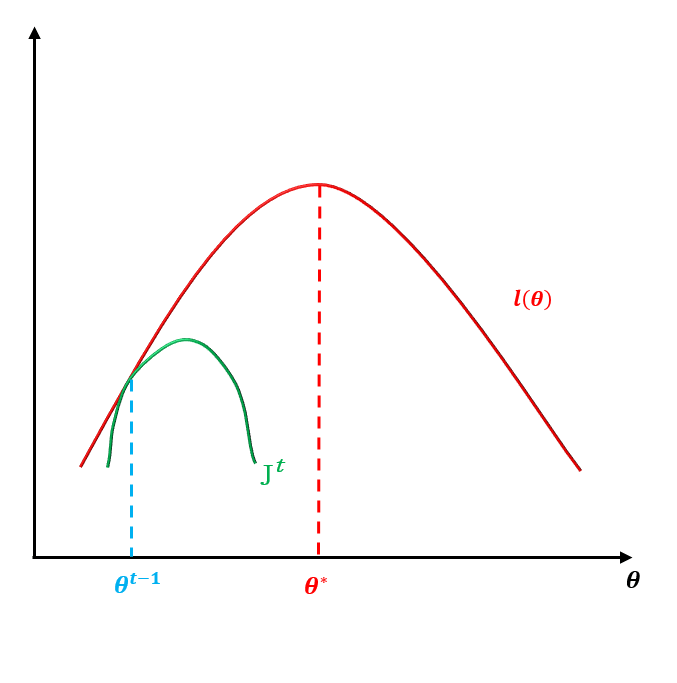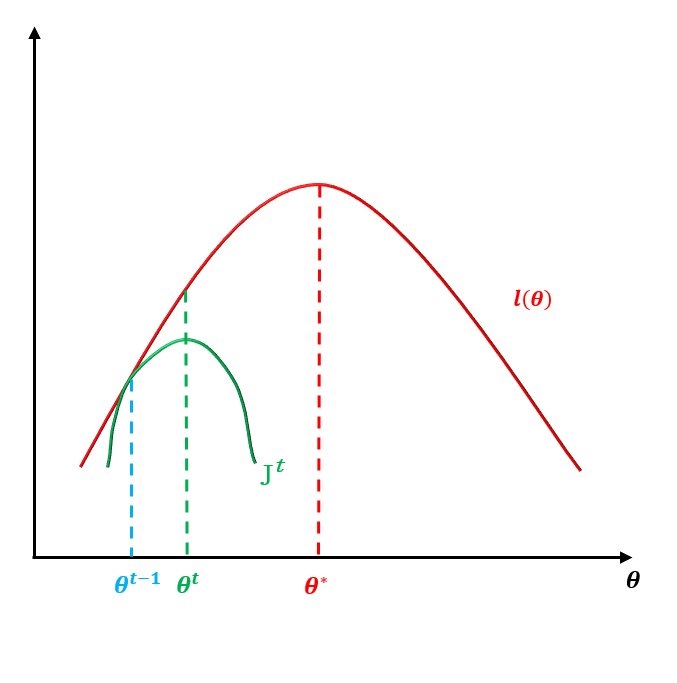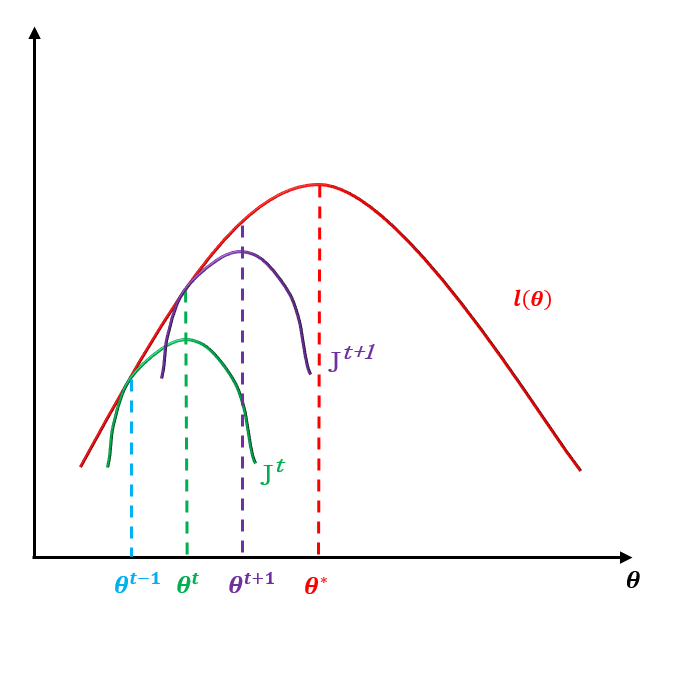
此时固定$Q_i$，调整$\theta$使下界$J(Q_i,\theta)$达到最大值。此时为新的$\theta$，再固定$\theta$，调整$Q_i$……直到收敛到似然函数$l(\theta)$的最大值处的$\theta^*$。

整个过程如下图所示：

在$\theta$确定的时候，为了能让下界$J(Q_i,\theta)$逼近$l(\theta)$，需要Jensen不等式的等号成立。由证明过程可得等号成立的条件为

$$\dfrac{p(x_i,z_i;\theta)}{Q_i(z_i)}=c$$
此时可得
$$\sum_{z_i}{p(x_i,z_i;\theta)}=c\sum_{z_i}{Q_i(z_i)}=c$$
代入上式
$$\begin{align*} Q_i(z_i)&=\dfrac{p(x_i,z_i;\theta)}{\sum\limits_{z_i}{p(x_i,z_i;\theta)}}\\ &=\dfrac{p(x_i,z_i;\theta)}{p(x_i;\theta)}\\ &=p(z_i|x_i;\theta) \end{align*}$$
至此，我们推出了在固定其他参数 $\theta$后， $Q_i(z_i)$的计算公式就是后验概率，解决了 $Q_i(z_i)$如何选择的问题。这一步就是E步，建立 $l(\theta)$的下界。

接下来的M步，就是在给定$Q_i(z_i)$后，调整$\theta$，去极大化$l(\theta)$的下界。

算法步骤

• 给定$\theta$的初值$\theta^0$
• E步：对于每一个样本$x_i$，通过$\theta^{(t)}$得到$Q_i^{(t)}(z_i)$： $$Q_i^{(t)}(z_i):=p(z_i|x_i;\theta^{(t)})$$
• M步：通过$Q_i^{(t)}(z_i)$计算的到$\theta^{(t+1)}$： $$\begin{align*}\theta^{(t+1)}&:=\arg\max_{\theta}\sum_{i}{\sum_{z_i}{Q_i^{(t)}(z_i)\ln\dfrac{p(x_i,z_i;\theta)}{Q_i^{(t)}(z_i)}}}\\&:=\arg\max_{\theta}\sum_{i}{\sum_{z_i}{Q_i^{(t)}(z_i)\ln p(x_i,z_i;\theta)}}\end{align*}$$

算法的另一种表述

• 给定$\theta$的初值$\theta^{(0)}$
• E步：通过给定的$\theta^{(t)}$得到$\ln p(x,z;\theta)$的关于$z$的期望
  $$\begin{align*}H(\theta,\theta^{(t)})&:=E_{z|x,\theta^{(t)}}[\ln p(x,z;\theta)]\\&:=\sum_z{p(z|x;\theta^{(t)})\ln p(x,z;\theta)}\end{align*}$$
• M步: 计算
  $$\theta^{(t+1)}:=\arg\max_{\theta}H(\theta,\theta^{(t)})$$