EM算法推导及案例演示

醉糊涂仙

已于 2023-08-16 09:05:33 修改

阅读量816

点赞数 4

文章标签：算法

于 2023-08-12 10:25:34 首次发布

本文链接：https://blog.csdn.net/u010916338/article/details/132244841

版权

一、必备的基础知识

EM算法用到了大量的概率论与数理统计的知识，必须对基础有一定掌握才能完成EM算法的推导。

1.1 最大似然估计

思想：我们观测到了一组样本，为什么我们能观测到这一组样本呢？因为这一组样本出现的概率比较大，如果这一组观测值出现的概率比较小我们很可能就观测不到这组样本。基于以上理论，我们先将这组样本出现的概率求出来，前面提到这组样本出现的概率比较大我们才能观测到这组样本，那么多大的概率才算是概率比较大呢？我们没有概念，但是我们可以求出现这组样本的最大概率，这个最大概率的值是多少我们并不关心，在求概率最大的过程中就可以将概率分布中的参数θ求出来。

总结：最大似然估计就是令观测到的样本出现的概率最大，在求概率最大值的过程中对参数θ求导，令导数为零，进而求出参数θ。

权威的最大似然估计解释见下图：

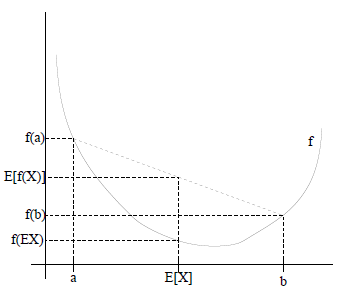
1.2 Jensen不等式

（1）凹函数和凸函数：首先问大家一个问题，下面的函数是凹函数还是凸函数？不太好回答，因为不同的教材里面对于凹函数和凸函数的正方向的定义不太相同，所以本博客统一规定：上凸函数即下凹函数；上凹函数即下凸函数。那么下图就是一个上凹下凸的函数。

（2）上凹下凸函数： $f(EX) \leqslant E[f(X)]$ （证明略···）

1.3 贝叶斯公式

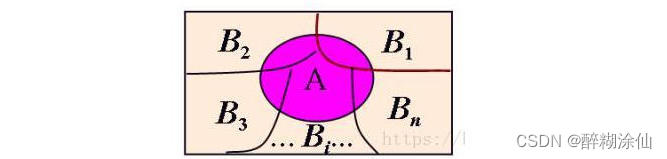
1.4 边缘分布

1.5 总体、个体、样本、样本值

总体：试验的全部可能的观察值称为总体，这些观察值可能有重复值（如果将这些值去重，就是样本空间，样本空间是一个集合，不重复）。

总体和随机变量：总体和随机变量可以划等号，一个总体对应一个随机变量X，可以称为总体X。

个体：对总体X进行的一次观察，并记录的结果。

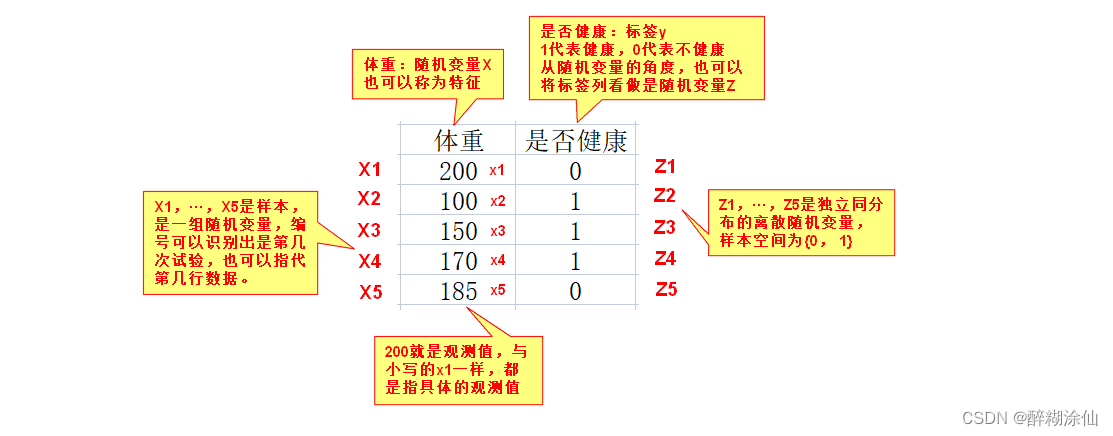
样本：对总体X进行n次重复的、独立的试验，每一次试验用一个随机变量Xi表示（此时还没有做试验，先用变量表示），n次试验结果按照试验顺序排列记为X1，X2，···，Xn。我们称X1，X2，···，Xn就是来自总体X的一个随机样本。（注意Xi仅仅代表第i次试验对应的随机变量，并不是指具体的值，其实质还是一个随机变量，只是编上了号而已，且Xi与X是独立同分布）。

样本值：当n次观察一经完成，我们就得到了一组实数x1，x2，···，xn，他们依次是随机变量X1，X2，···，Xn的观察值，称为样本值。

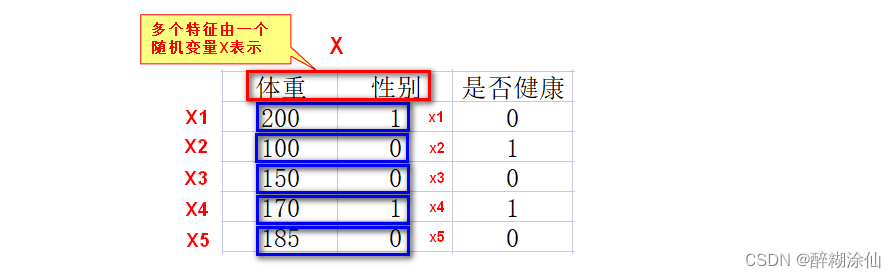
另外，需要注意的是一个随机变量X可以表示多个特征（在《数据挖掘十大算法》一书中有所体现）

1.6 期望

注意：期望又称均值，这里的均值指的是总体的均值，跟样本均值不是一个概念。

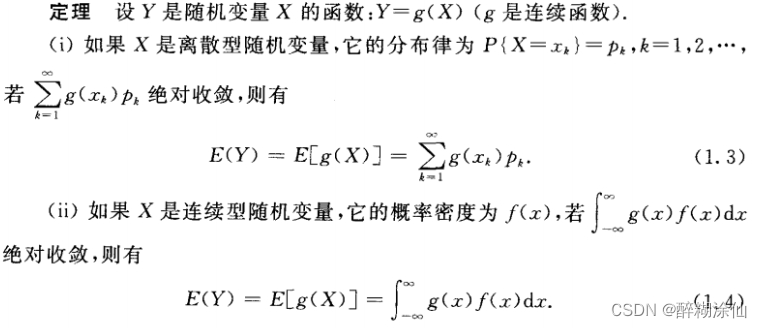
二、EM算法推导

背景：在没有隐变量的情况下，使用最大似然估计MLE即可估计出概率分布的参数θ，但是当存在隐变量时最大似然估计法也束手无策，EM算法可以在有隐变量的情况下同时估计出参数θ和隐变量的分布。

隐变量：前文提到隐变量，那么到底什么是隐变量？有机器学习基础的同学一看就懂，这里提到的隐变量其实就是标签（类别），一个观察值样本X，可以看做是特征数据（字段），那么每一行数据都对应一个y值，即标签（类别），于是就可以将（X, y）看成是一个观察样本。然后再通过最大似然估计思想，假设该样本出现的概率最大时，将参数θ和隐变量的分布同时求出来。（如果没有机器学习的基础，建议去了解有监督和无监督的概念）

用途：无监督学习，可以实现聚类的效果。

2.1 带有隐变量的最大似然估计

设，X1，X2，X3···Xn是来自总体X的1个样本；设x1，x2，x3···xn是来自样本X1，X2，X3···Xn的一个样本值（观察值）；设Zi是类别（标签）对应每一个Xi。

于是，观测样本X，隐变量Z，完整观测样本（X，Z）。

$L(\theta )=\prod_{i=1}^{n}p(x_{i};\theta )$ 概率乘积

$\Rightarrow lnL(\theta )=\sum_{i=1}^{n}lnp(x_i;\theta )$ 取对数

$\Rightarrow ln^{L(\theta )}=\sum_{i=1}^{n}ln\sum_{z_i}p(x_i,z_i;\theta )$ 边缘分布

假设，第i次试验的随机变量Xi对应的隐变量Zi服从Qi(zi)分布，则：

$\Rightarrow ln^{L(\theta )}=\sum_{i=1}^{n}ln\sum_{z_i}Q_i(zi)\frac{p(x_i,z_i;\theta)}{Q_i(zi)}$ 乘以再除以，结果不变

$\because EX=\sum p(x)\cdot x$

$\because E[f(x)]=\sum p(x)\cdot f(x)$

$Qi(zi)$ 表示计算概率，等同于 $p(x)$ ， $\frac{p(x_i,z_i;\theta)}{Q_i(zi)}$ 等同于一个函数 $f(x)$

$\Rightarrow ln^{L(\theta )}=\sum_{i=1}^{n}lnE[\frac{p(x_i,z_i;\theta)}{Q_i(zi)}]$

$\because \sum_{i=1}^{n}lnE[\frac{p(x_i,z_i;\theta)}{Q_i(zi)}]\geq \sum_{i=1}^{n}E[ln\frac{p(x_i,z_i;\theta)}{Q_i(zi)}]$ jesen不等式（ln函数是一个上凸下凹的函数）

$\because \sum_{i=1}^{n}E[ln\frac{p(x_i,z_i;\theta)}{Q_i(zi)}] = \sum_{i=1}^{n}\sum_{zi}Q_i(zi)ln\frac{p(x_i,z_i;\theta)}{Q_i(zi)}$ 期望公式变换

$\Rightarrow lnL(\theta ) \geq \sum_{i=1}^{n}\sum_{zi}Q_i(zi)ln\frac{p(x_i,z_i;\theta)}{Q_i(zi)}$

2.2 间接求似然函数的最大值

我们的目标是将 $lnL(\theta )$ 最大化，但是现在知道 $lnL(\theta )$ 的下界函数，这个函数一直小于等于 $lnL(\theta )$ ，于是我们变换思路，求下界函数的最大值，在求下界函数最大值的过程中，不断逼近 $lnL(\theta )$ 的最大值（注意，下界函数不是求一次最大值就完事儿了，EM算法本身就是一个迭代算法，下界函数也一直在变动）

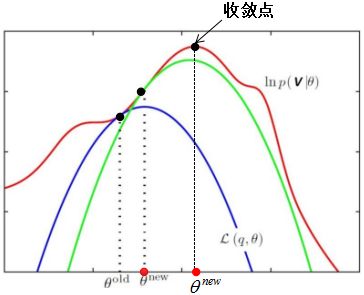
那么，下界函数的最大值怎么求呢？从形式上看，即 $lnL(\theta )$ 与下界函数相等的时候，下界函数就会取到最大值，即：

$ln^{L(\theta )}=\sum_{i=1}^{n}ln\sum_{z_i}Q_i(zi)\frac{p(x_i,z_i;\theta)}{Q_i(zi)}= ?=\sum_{i=1}^{n}\sum_{zi}Q_i(zi)ln\frac{p(x_i,z_i;\theta)}{Q_i(zi)}$

$\Rightarrow ln^{L(\theta )}=\sum_{i=1}^{n}lnE[\frac{p(x_i,z_i;\theta)}{Q_i(zi)}]=?=\sum_{i=1}^{n}E[ln\frac{p(x_i,z_i;\theta)}{Q_i(zi)}]$

$\Rightarrow lnE[\frac{p(x_i,z_i;\theta)}{Q_i(zi)}]=?=E[ln\frac{p(x_i,z_i;\theta)}{Q_i(zi)}]$

$f(EX)=?=E[f(X)]$

当f(x)为常数时，等号成立，这里的f(x)即ln(x)，ln(x)为常数即x为常数，即：

$\frac{p(x_i,z_i;\theta)}{Q_i(zi)}=C$

$\Rightarrow p(x_i,z_i;\theta)=C\cdot Q_i(zi)$

$\Rightarrow \sum_{zi} p(x_i,z_i;\theta)=C\cdot \sum_{zi}Q_i(zi)$

$\because \sum_{zi}Q_i(zi)=1$

$\therefore \sum_{zi} p(x_i,z_i;\theta)=C$

$\frac{p(x_i,z_i;\theta)}{Q_i(zi)}=C\Rightarrow Q_i(zi)=\frac{p(x_i,z_i;\theta)}{C}$

$\Rightarrow Q_i(zi)=\frac{p(x_i,z_i;\theta)}{\sum_{zi} p(x_i,z_i;\theta)}$ 替换C

$\Rightarrow Q_i(zi)=\frac{p(x_i,z_i;\theta)}{p(x_i;\theta)}$ 边缘分布

$\Rightarrow Q_i(zi)=p(z_i|x_i;\theta)$ 条件概率

2.3 贝叶斯求所属类别的概率

到这个地方，就可以把类别的概率分布求出来，首先假设θ已知（初始化），再求出这个条件概率即可，那么这个条件概率如何理解呢？通过贝叶斯转换来求！！！这时，必须理解这里的zi是什么意思， $zi$ 指的是第i次试验随机变量 $Xi$ 对应的标签（类别）随机变量 $Zi$ 的一个具体观测个体值，那么随机变量 $Zi$ 的所有取值，就是所有的类别或者标签取值，假设有m个类别，那么 $z_{1}$ ， $z_{2}$ ，···， $z_{i}$ ，···， $z_{m}$ 就是样本空间的一个划分，到这里就明白了，求已知观测个体 $xi$ 的条件下属于某个类别（标签） $zi$ 的概率，可以先分别求在所有类别的情况下观测到xi的概率，然后通过贝叶斯反推出要求的结果，大家可以结合后面的案例一起来看。

$\Rightarrow Q_i(zi)=p(z_i|x_i;\theta)=\frac{p(xi|zi:\theta )\cdot p(zi)}{\sum_{i=1}^{m}p(xi|zi:\theta )p(zi)}$

2.4 E步和M步

综上，有两个地方需要特别注意：

（1）E步：初始化参数θ，利用贝叶斯求出概率分布 $Q_i(zi)$

$Q_i(zi)=p(z_i|x_i;\theta)=\frac{p(xi|zi:\theta )\cdot p(zi)}{\sum_{i=1}^{m}p(xi|zi:\theta )p(zi)}$

（2）M步：代入 $Q_i(zi)$ ，在求下界函数的最大值过程中，求出新的参数θ值。

$argmax\sum_{i=1}^{n}\sum_{zi}Q_i(zi)ln\frac{p(x_i,z_i;\theta)}{Q_i(zi)}$

2.5 下界函数收敛性

不断迭代E步和M步，直到 $\sum_{i=1}^{n}\sum_{zi}Q_i(zi)ln\frac{p(x_i,z_i;\theta)}{Q_i(zi)}$ 收敛

即，保证：

$\sum_{i=1}^{n}\sum_{zi}Q_i(zi)ln\frac{p(x_i,z_i;\theta^{t+1})}{Q_i(zi)}\geq \sum_{i=1}^{n}\sum_{zi}Q_i(zi)ln\frac{p(x_i,z_i;\theta^{t})}{Q_i(zi)}$

从而：

$lnL(\theta ^{t+1})\geq lnL(\theta ^{t})$

三、案例

笔者综合网上案例，发现下面这个案例比较好，但是想完全理解也需要下一番功夫。

3.1 不包含隐变量

假设有两枚硬币1和2，他们随机抛掷后正面朝上的概率分别为 $\theta _{A}$ 、 $\theta _{B}$ 。这里不包含隐变量的意思是每次抛掷都知道是哪一个硬币被抛掷，我们能很清楚知道样本观测值来自哪一枚硬币（即属于哪一类）。于是，我们只需要通过试验，估计出 $\theta _{A}$ 和 $\theta _{B}$ 的值即可，试验定义如下：每次取一枚硬币，连续抛掷5下记为一组，共抛掷五组，记录结果如下：

硬币	结果	统计
1	正正反正反	3正-2反
2	反反正正反	2正-3反
1	正反反反反	1正-4反
2	正反反正正	3正-2反
1	反正正反反	2正-3反

由于，两个硬币抛掷互不干扰，所以我们以抛掷硬币1为例来演示 $\theta _{A}$ 的最大似然估计。

硬币1的分布律形式已知，如下图所示，分布律中的参数 $\theta _{A}$ 未知：

X	正面	反面
p	$\theta _{A}$	$1-\theta _{A}$

硬币1的试验结果统计如下表：

硬币	结果	统计
1	正正反正反	3正-2反
1	正反反反反	1正-4反
1	反正正反反	2正-3反

那么出现以上结果的概率为：

$L(\theta_{A} )=(\theta _{A})^3(1-\theta _{A})^2\cdot (\theta _{A})(1-\theta _{A})^4\cdot (\theta _{A})^2(1-\theta _{A})^3$

$\Rightarrow L(\theta_{A} )=(\theta _{A})^6(1-\theta _{A})^9$

对似然函数取对数：

$ln L(\theta_{A} )=6ln(\theta _{A})+9ln(1-\theta _{A})$

令 $\frac{d}{d\theta _{A}}ln L(\theta _{A})=\frac{6}{\theta _{A}}-\frac{9}{1-\theta _{A}}=0$

$\Rightarrow\hat{ \theta _{A}}=\frac{6}{15}=0.4$

对于 $\theta _{A}$ 的估计，其它博客采用的方法是用硬币1出现的次数除以硬币1抛掷的总次数，计算方式如下面公式，笔者为了演示EM算法流程所以采用了较为详细的最大似然估计流程，为了方便计算便于书写，笔者后续也会采用如下计算方法。

$\hat{\theta _{A}}=\frac{3+1+2}{15}=0.4$

3.2 包含隐变量

试验定义如下：每次取一枚硬币，连续抛掷5下记为一组，共抛掷五组，每一组为同一枚硬币，但是不知道是哪一枚硬币抛掷的，记录结果如下：

硬币	结果	统计
unknown	正正反正反	3正-2反
unknown	反反正正反	2正-3反
unknown	正反反反反	1正-4反
unknown	正反反正正	3正-2反
unknown	反正正反反	2正-3反

那么这里不光要估计出两枚硬币正面朝上的概率 $\theta _{A}$ 、 $\theta _{B}$ ，还要估计出样本个体所属类别的概率分布 $Q_i(zi)$ ，由于硬币所属类别是一个离散随机变量 $Zi$ ，所以求出的 $Q_i(zi)$ 其实是一个分布律。

根据前面推导的公式可得：

$Q_i(zi)=p(z_i|x_i;\theta)=\frac{p(xi|zi:\theta )\cdot p(zi)}{\sum_{i=1}^{m}p(xi|zi:\theta )p(zi)}$

（1）初始化θ，令 $\theta _A=0.2$ ， $\theta _B=0.7$ （初始化是随机的）

（2）基础初始化的θ求 $p(xi|zi;\theta )$ ，这里指的是知道硬币归属（类别）的情况下观测到当前样本个体的概率，需要注意的是 $xi$ 指的是样本中第 $i$ 个个体，这里指的就是第 $i$ 组试验观测结果，一共五组试验称为一个样本，但是这里的 $zi$ 却有两个值（即类别的个数，硬币1或硬币2），我们令 $zi=1$ 代表硬币1， $zi=2$ 代表硬币2， $zi=1$ 和 $zi=2$ 就是随机变量 $Zi$ 样本空间的一个划分。

我们以第一组试验为例讲解 $p(xi|zi;\theta )$ 的计算。

硬币1出现正正反正反的概率为：

$p(xi|zi=1;\theta )0.2*0.2*0.8*0.2*0.8=0.00512$

硬币2出现正正反正反的概率为：

$p(xi|zi=2;\theta )0.7*0.7*0.3*0.7*0.3=0.03087$

将所有组（轮次）试验的结果分别计算，统计如下表：

轮次	结果	统计	硬币1产生此结果的概率	硬币2产生此结果的概率
1	正正反正反	3正-2反	0.00512	0.03087
2	反反正正反	2正-3反	0.02048	0.01323
3	正反反反反	1正-4反	0.08192	0.00567
4	正反反正正	3正-2反	0.00512	0.03087
5	反正正反反	2正-3反	0.02048	0.01323

（3）根据贝叶斯求 $p(zi|xi;\theta )$ ，以第一组试验为例讲解：

$p(zi=1|xi;\theta )=\frac{p(xi|zi=1;\theta )p(zi=1)}{\sum_{zi}p(xi|zi;\theta )p(zi)}=\frac{p(xi|zi=1;\theta )p(zi=1)}{p(xi|zi=1;\theta )p(zi=1)+p(xi|zi=2;\theta )p(zi=2)}$

注意：笔者参考了大量博客都没有提到 $p(zi=1)$ 和 $p(zi=2)$ 的计算，这里假定选中硬币1和硬币2的概率一样，即 $p(zi=1)$ 和 $p(zi=2)$ 的概率都是0.5。

已知试验结果“正正反正反”，求该结果是硬币1投掷的概率：

$p(zi=1|xi;\theta )=\frac{p(xi|zi=1;\theta )}{p(xi|zi=1;\theta )+p(xi|zi=2;\theta )}=\frac{0.00512}{0.00512+0.03087}=0.14$

$p(zi=2|xi;\theta )=\frac{p(xi|zi=2;\theta )}{p(xi|zi=1;\theta )+p(xi|zi=2;\theta )}=\frac{0.03087}{0.00512+0.03087}=0.86$

将所有组（轮次）试验的结果分别计算，统计如下表：

轮次	结果	统计	已知此结果，推测是由硬币1投掷的概率	已知此结果，推测是由硬币2投掷的概率
1	正正反正反	3正-2反	0.14	0.86
2	反反正正反	2正-3反	0.61	0.39
3	正反反反反	1正-4反	0.94	0.06
4	正反反正正	3正-2反	0.14	0.86
5	反正正反反	2正-3反	0.61	0.39

上面这个表其实就是 $Q_i(zi)$ 的概率分布，因为Zi是一个离散的随机变量，所以 $Q_i(zi)$ 其实是一个分布律。

（4）计算M步，即：

$argmax\sum_{i=1}^{n}\sum_{zi}Q_i(zi)ln\frac{p(x_i,z_i;\theta)}{Q_i(zi)}$

$=Q_1(zi=1)ln\frac{p(x1,zi=1;\theta )}{Q_1(zi=1)}+Q_1(zi=2)ln\frac{p(x1,zi=2;\theta )}{Q_1(zi=2)}\\ +Q_2(zi=1)ln\frac{p(x2,zi=1;\theta )}{Q_2(zi=1)}+Q_2(zi=2)ln\frac{p(x2,zi=2;\theta )}{Q_2(zi=2)}\\ +\cdot \cdot \cdot \cdot \cdot \cdot \\ +Q_5(zi=1)ln\frac{p(x5,zi=1;\theta )}{Q_5(zi=1)}+Q_5(zi=2)ln\frac{p(x5,zi=2;\theta )}{Q_5(zi=2)}$

$Q_i(zi)$ 可以根据前面求出的分布律直接带入， $p(x1,zi=1;\theta )$ 代表的是用硬币1投掷出现 $x1$ 的概率，我们依然假设两枚硬币1和2，他们随机抛掷后正面朝上的概率分别为 $\theta _{A}$ 、 $\theta _{B}$ ，那么 $p(x1,zi=1;\theta )={\theta _A}^3(1-\theta _A)^2$ ，以此类推将 $Q_i(zi)$ 和 $p(x1,zi=1;\theta )$ 分别带入，可得：

$=0.14ln\frac{{\theta _A}^3(1-\theta _A)^2}{0.14}+0.86ln\frac{{\theta _B}^3(1-\theta _B)^2}{0.86}\\ +0.61ln\frac{{\theta _A}^2(1-\theta _A)^3}{0.61}+0.39ln\frac{{\theta _B}^2(1-\theta _B)^3}{0.39}\\ +\cdot \cdot \cdot \cdot \cdot \cdot \\ +0.61ln\frac{{\theta _A}^2(1-\theta _A)^3}{0.61}+0.39ln\frac{{\theta _B}^2(1-\theta _B)^3}{0.39}$

$=0.28ln\frac{{\theta _A}^3(1-\theta _A)^2}{0.14}+1.72ln\frac{{\theta _B}^3(1-\theta _B)^2}{0.86}\\ +1.22ln\frac{{\theta _A}^2(1-\theta _A)^3}{0.61}+0.78ln\frac{{\theta _B}^2(1-\theta _B)^3}{0.39}\\ +0.94ln\frac{{\theta _A}(1-\theta _A)^4}{0.94}+0.06ln\frac{{\theta _B}(1-\theta _B)^4}{0.06}$

我们的目标是将上面式子最大化，在最大化的过程中求出参数 $\theta _{A}$ 和 $\theta _{B}$ ，为了方便求偏导数，我们将上面式子拆开，因为对 $\theta _{A}$ 求偏导数，包含 $\theta _{B}$ 的部分求导都为零， $\theta _{B}$ 部分就不再展示：

$=0.28(ln{\theta_A}^3+ln(1-\theta _A)^2-ln0.14)\\ +1.22(ln{\theta_A}+ln(1-\theta _A)^3-ln0.61)\\ +0.94(ln\theta_A+ln(1-\theta _A)^4-ln0.94)\\ +\cdot \cdot \cdot \cdot \cdot \cdot$

$\frac{\partial argmax}{\partial \theta _A}\\= \frac{0.28\times 3}{\theta _A}-\frac{0.28\times2}{1-\theta _A}\\ +\frac{1.22\times2}{\theta _A}-\frac{1.22\times3}{1-\theta _A}\\ +\frac{0.94}{\theta _A}-\frac{0.94\times4}{1-\theta _A}$

令 $\frac{\partial argmax}{\partial \theta _A}=\frac{4.22-12.2\theta _A}{\theta _A(1-\theta _A)}=0$

$\theta _A\approx 0.35$

相同的方法可求得， $\theta _B\approx 0.53$

（5）新算的 $\theta _{A}$ 和 $\theta _{B}$ 替换掉初始化值，重复（1）···（5）步，直到 $\theta _{A}$ 和 $\theta _{B}$ 不再变化。

醉糊涂仙

关注

4
点赞
踩
4

收藏

觉得还不错? 一键收藏
0
评论
EM算法推导及案例演示

因为这一组样本出现的概率比较大，如果这一组观测值出现的概率比较小我们很可能就观测不到这组样本。基于以上理论，我们先将这组样本出现的概率求出来，前面提到这组样本出现的概率比较大我们才能观测到这组样本，那么多大的概率才算是概率比较大呢？我们没有概念，但是我们可以求出现这组样本的最大概率，这个最大概率的值是多少我们并不关心，在求概率最大的过程中就可以将概率分布中的参数θ求出来。总结：最大似然估计就是令观测到的样本出现的概率最大，在求概率最大值的过程中对参数θ求导，令导数为零，进而求出参数θ。
复制链接

扫一扫