EM算法理解与推导

首先我们开门见山，EM算法到底是干什么的，EM算法是在面对一个含有隐变量的概率模型，是一种迭代算法，目标就是极大化观测数据关于参数的对数似然函数。
这么说可能很难理解，我们来举一个例子吧，就拿抛硬币来说，假设有A和B两枚硬币，要估计的参数是它们各自翻正面的概率。观察的过程是先随机选择硬币A或者B，然后连续扔10次，重复此步骤5次。意思就是说有两枚硬币，只知道抛出之后的分布，但是不知道是哪个硬币抛出的，我们应该如何估计观测值分布的概率是多少呢？

序号	硬币	正反分布	CoinA	CoinB
1	B	正 反 反 反 正 正 反 正 反 正	-	5正 5反
2	A	正 正 正 正 反 正 正 正 正 正	9正 1反	-
3	A	正 反 正 正 正 正 正 反 正 正	8正 2反	-
4	B	正 反 正 反 反 反 正 正 反 反	-	4正 6反
5	A	反 正 正 正 反 正 正 正 反 正	7正 3反	-

a.极大似然估计

假设我们的观测值Y分布如上表所示，那么总的来说，硬币A抛出了24正6反的分布，B抛出了9正11反的分布，所以我们可以计算在这个分布的情况下，硬币A与B的正面朝上的概率：
$${\hat{\theta }}_A\text{ = }\frac{24}{24\text{ + }6}\text{ = }0.8$$
$${\hat{\theta }}_B\text{ = }\frac{9}{9\text{ + }11}\text{ = }0.45$$
这只是一个大概估计的数值，我们可以把这里计算的结果放到后面作为估计硬币A和B正面朝上概率的一个参考。

b.EM期望最大化

首先我们根据上一步的估计，我们假设 ${\hat{\theta }}_A^{(0)}=0.6$，${\hat{\theta }}_B^{(0)}=0.5$，这里的上角标(0)表示第一轮的迭代，也表示初始的输入值。我们假设不知道这个观测值是由哪个硬币抛出的结果，那么我们就根据正反的分布来估计一下。比如上表中的第二个9正1反的分布，我们怎么判断是来自哪个硬币抛出的结果呢？
首先我们，计算A和B硬币抛出此分布的概率：
$$P(A)=C_{10}^9({\hat{\theta }}_A^{(0)}{)}^9(1-{\hat{\theta }}_A^{(0)})=10(0.6{)}^9(0.4)\approx 0.04031$$
$$P(B)=C_{10}^9({\hat{\theta }}_B^{(0)}{)}^9(1-{\hat{\theta }}_B^{(0)})=10(0.5{)}^9(0.5)\approx 0.00976$$
综上所述，此分布来自A的概率为：
$$P(fromA)=\frac{P(A)}{P(A)+P(B)}\approx 0.8$$
$$P(fromB)=\frac{P(B)}{P(A)+P(B)}\approx 0.2$$
有了这个来源的概率之后，我们就可以计算每一种观测分布的期望值了，就还是拿第二个9正1反的分布来说，那么硬币A的分布期望就是正 0.8 * 9 = 7.2 次，反 0.8 * 1 = 0.8 次，硬币B的分布期望就是正 0.2 * 9 = 1.8 次， 反 0.2 * 1 = 0.2 次，以此类推，我们可以得到在这种观测概率分布的情况下，第一轮硬币A和B的期望值：

序号	来源分布	CoinA	CoinB
1	0.45 from A 0.55 from B	2.2正 2.2反	2.8正 2.8反
2	0.80 from A 0.20 from B	7.2正 0.8反	1.8正 0.2反
3	0.73 from A 0.27 from B	5.9正 1.5反	2.1正 0.5反
4	0.35 from A 0.65 from B	1.4正 2.1反	2.6正 3.9反
5	0.65 from A 0.35 from B	4.5正 1.9反	2.5正 1.1反
total	-	21.3正 8.6反	11.7正 8.4反

我们接着就可以统计出硬币A和B的抛出正反面的概率，这就进行了一次迭代的过程，会更新我们的${\hat{\theta }}_A$和${\hat{\theta }}_B$：
$${\hat{\theta }}_A^{(1)}=\frac{21.3}{21.3+8.6}\approx 0.71$$
$${\hat{\theta }}_B^{(1)}=\frac{11.7}{11.7+8.4}\approx 0.58$$
这就是经过一次迭代之后的硬币A和B的抛出正面的概率，接着我们把 ${\hat{\theta }}_A^{(1)}$和 ${\hat{\theta }}_B^{(1)}$的结果再放到观测值的分布中再次进行硬币A和B的正反期望的运算，就会得到 ${\hat{\theta }}_A^{(2)}$和 ${\hat{\theta }}_B^{(2)}$，一直迭代下去直到收敛，最后得到的 ${\hat{\theta }}_A^{(n)}$和 ${\hat{\theta }}_B^{(n)}$就是我们从观测值Y中得到的硬币A和B的抛到正面的概率。
有了这个抛硬币的例子，相信大家对EM算法有了基本的理解了，接下来我们用公式来推导一下，加深对EM算法的理解。在前面也有说过，EM算法的目的就是极大化观测数据 $Y$关于参数 $\theta$的对数似然函数的，在这个过程中含有隐含的变量 $Z$,比如我们的硬币A和B的随机选择就是一个隐含的变量。总的来说，就是极大化下面这个表达式：
$$L(\theta )=\log P(Y|\theta )=\log \sum _{Z}P(Y,Z|\theta )$$
这个表达式同样可以写成：
$$\log \sum _{Z}P(Y,Z|\theta )=\log \sum _{Z}P(Y|Z,\theta )P(Z|\theta )$$
由上述的内容我们可以知道，EM算法是通过迭代的方式来极大化 $L(\theta )$的，假设在第 $i$次迭代之后的 $\theta$估计值为 ${\theta }^{(i)}$，我们希望的是每迭代一次，参数 $\theta$就离真实值更近一步，$L(\theta )$就会更大一些，知道最后 $L(\theta )$收敛，那么就可以得到如下表达式：
$$L(\theta )-L({\theta }^{(i)})=\log [\sum _{Z}P(Y|Z,\theta )P(Z|\theta )]-\log P(Y|{\theta }^{(i)})$$
我们将上述表达式进行变换可以得到：
$$\log [\sum _{Z}P(Y|Z,\theta )P(Z|\theta )]-\log P(Y|{\theta }^{(i)})=\log [\sum _{Z}P(Z|Y,{\theta }^{(i)})\frac{P(Y|Z,\theta )P(Z\text{|}\theta )}{P(Z|Y,{\theta }^{(i)})}]-\log P(Y|{\theta }^{(i)})$$
到这里我们可以运用简森不等式的特性：
$$\log \sum _j{\lambda }_j{y}_j⩾\sum _j{\lambda }_j\log y_j;{\lambda }_j⩾0,\sum _j{\lambda }_j=1$$
可以将上述表达式变换成：
$$\begin{gathered} \log [\sum _{Z}P(Z|Y,{\theta }^{(i)})\frac{P(Y|Z,\theta )P(Z\text{|}\theta )}{P(Z|Y,{\theta }^{(i)})}]-\log P(Y|{\theta }^{(i)}) \\ ⩾\sum _{Z}P(Z|Y,{\theta }^{(i)})\log \frac{P(Y|Z,\theta )P(Z|\theta )}{P(Z|Y,{\theta }^{(i)})}-\log P(Y|{\theta }^{(i)}) \\ =\sum _{Z}P(Z|Y,{\theta }^{(i)})\log \frac{P(Y|Z,\theta )P(Z|\theta )}{P(Z|Y,{\theta }^{(i)})P(Y|{\theta }^{(i)})} \end{gathered}$$
我们可以令：
$$B(\theta ,{\theta }^{(i)})=L({\theta }^{(i)})+\sum _{Z}P(Z|Y,{\theta }^{(i)})\log \frac{P(Y|Z,\theta )P(Z|\theta )}{P(Z|Y,{\theta }^{(i)})P(Y|{\theta }^{(i)})}$$
由上述的不等式可知:
$$L(\theta )⩾B(\theta ,{\theta }^{(i)})$$
那么可以知道$B(\theta ,{\theta }^{(i)})$是$L(\theta )$的下界，同时$L({\theta }^{(i)})=B({\theta }^{(i)},{\theta }^{(i)})$，所以任何可以使$B(\theta ,{\theta }^{(i)})$增长的 $\theta$，也可以使$L(\theta )$增大，为了让$L(\theta )$有尽可能大的增长，我们选择 ${\theta }^{(i+1)}$使 $B(\theta ,{\theta }^{(i)})$达到极大，那么就可以将${\theta }^{(i+1)}$表达成：
$${\theta }^{(i+1)}=\arg \underset{\theta }{\max }(L({\theta }^{(i)})+\sum _{Z}P(Z|Y,{\theta }^{(i)})\log \frac{P(Y|Z,\theta )P(Z|\theta )}{P(Z|Y,{\theta }^{(i)})P(Y|{\theta }^{(i)})})$$
此表达式可以继续简化，去掉表达式中不相关的常数：
$${\theta }^{(i+1)}=\arg \underset{\theta }{\max }(\sum _{Z}P(Z|Y,{\theta }^{(i)})\log P(Y|Z,\theta )P(Z|\theta ))=\arg \underset{\theta }{\max }(\sum _{Z}P(Z|Y,{\theta }^{(i)})\log P(Y,Z|\theta ))$$
我们令：$$Q(\theta ,{\theta }^{(i)})=\sum _{Z}P(Z|Y,{\theta }^{(i)})\log P(Y,Z|\theta )$$
那么：$${\theta }^{(i+1)}=\arg \underset{\theta }{\max }Q(\theta ,{\theta }^{(i)})$$
这整个的过程就相当于是EM算法的一次迭代，通过不断的迭代，去求Q函数的极大值。如下图是李航的统计学习方法中对EM算法的解释：

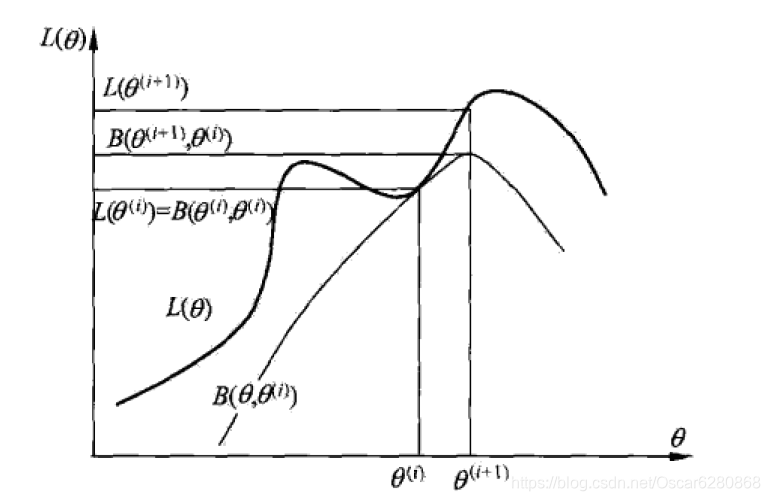
这里通过 ${\theta }^{(i)}$到 ${\theta }^{(i+1)}$的迭代，寻找 $B(\theta ,{\theta }^{(i)})$的极大值点，然后更新 $L(\theta )$，这个时候只能保证$L(\theta )$是增长的，但不能保证是全局最优的解，所以EM算法是无法保证全局最优解，从上图中也可以看出。
本文对EM算法做了一个详细的案例分析和过程推导，希望能够帮助大家理解EM的算法，同时文中如有纰漏，也请各位读者不吝指教，共同进步；如有转载，也请标明出处，谢谢。