poj 1659 Frogs' Neighborhood(贪心Havel-Hakimi可构造简单图定理)

poj 1659 Frogs’ Neighborhood(贪心Havel-Hakimi可构造简单图定理)
Time Limit: 5000ms Memory Limit: 65536kB

Description
未名湖附近共有n个大小湖泊L1, L2, …, Ln（其中包括未名湖），每个湖泊Li里住着一只青蛙Fi（1 <= i <= n）。如果湖泊Li和Lj之间有水路相连，则青蛙Fi和Fj互称为邻居。现在已知每只青蛙的邻居数目x1, x2, …, xn，请你给出每两个湖泊之间的相连关系。

Input
第一行是测试数据的组数t（0 <= t <= 20）。每组数据包括两行，第一行是整数n（2 <= n <= 10），第二行是n个整数，x1, x2,…, xn（0 <= xi < n）。

Output
对输入的每组测试数据，如果不存在可能的相连关系，输出”NO”。否则输出”YES”，并用n * n的矩阵表示湖泊间的相邻关系，即如果湖泊i与湖泊j之间有水路相连，则第i行的第j个数字为1，否则为0。每两个数字之间输出一个空格。如果存在多种可能，只需给出一种符合条件的情形。相邻两组测试数据之间输出一个空行。

Sample Input

3
7
4 3 1 5 4 2 1
6
4 3 1 4 2 0
6
2 3 1 1 2 1

Sample Output

YES
0 1 0 1 1 0 1
1 0 0 1 1 0 0
0 0 0 1 0 0 0
1 1 1 0 1 1 0
1 1 0 1 0 1 0
0 0 0 1 1 0 0
1 0 0 0 0 0 0

NO

YES
0 1 0 0 1 0
1 0 0 1 1 0
0 0 0 0 0 1
0 1 0 0 0 0
1 1 0 0 0 0
0 0 1 0 0 0

Source
POJ Monthly–2004.05.15 Alcyone@pku

---

本题一开始有模模糊糊看起来最优的解法的想法，后来发现这是图论中的一个定理。以下为摘录自http://www.cnblogs.com/jostree/p/4098136.html的证明:
给定一个非负整数序列D={d1,d2,…dn}，若存在一个无向图使得图中各点的度与此序列一一对应，则称此序列可图化。进一步，若图为简单图，则称此序列可简单图化。
可图化的判定为：d1+d2+⋯+dn=0(mod2)d1+d2+⋯+dn=0(mod2)。
即把奇数度的点配对，剩下的变为自环。
可简单图化的判定，即Havel-Hakimi定理：
我们把序列D变换为非增序列，即d1≥d2≥⋯≥dn，则D可简单图化当且仅当D′=(d2−1,d3−1,⋯,d(d1+1)−1,d(d1+2),d(d1+3),⋯,dn)可简单图化。

证明：
充分性：若D′可简单图化，把原图GD中的最大度点与GD′中度最大的d1个点连边即可，图GD必为简单图。
必要性：若D可简单图化，设得到的简单图为DG。分两种情况考虑:
(a)若GD中存在边(v1,v2),(v1,v3),…,(v1,vd1+1)(v1,v2),(v1,v3),…,(v1,vd1+1)，则删除这些边得简单图GD′，于是D′可简单图化为GD′
(b)若存在点vi,vj(i< j)且(v1,vi)不在GD中，但(v1,vj)在GD中。
这时，因为di≥dj，必存在k使得(vi,vk)在DG中但(vj,vk)不在GD中。这时我们可以令G′′=GD−{(vi,vk),(v1,vj)}+{(vk,vj),(v1,vi)}。G″的度序列仍为D，使用情况(a)处理。
证毕。

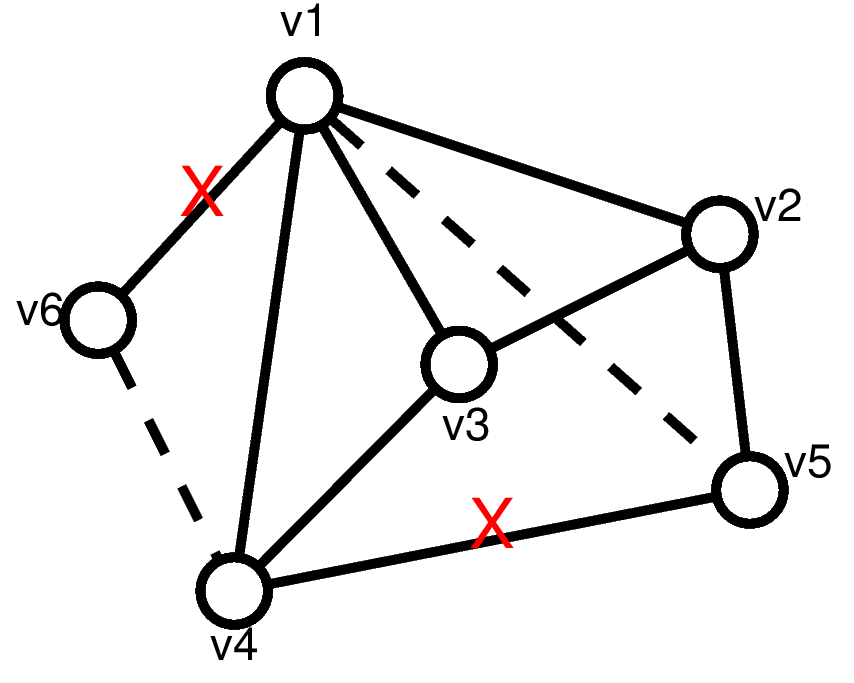
例如对于下图，我们删除两条打红X的边，添加两条虚线的边，即可转化为G′′

---

poj疑似有问题，评测无法AC

#define MAX_N 10

#include<stdio.h>
#include<stdlib.h>
#include<memory.h>

struct point_type
{
    int code;
    int deg;
};

int compare(const void* p1,const void* p2)
{
    const point_type* e1=(const point_type*) p1;
    const point_type* e2=(const point_type*) p2;
    return e2->deg-e1->deg;
}

int cases,n,flag;
point_type point[MAX_N+1];
int matrix[MAX_N+1][MAX_N+1];

void test()
{
    for (int i=1;i<=n;i++)
        printf("%d(%d)",point[i].deg,point[i].code);
    printf("\n"); 
}

int main()
{
    //freopen("input.txt","r",stdin); 
    scanf("%d",&cases);
    for (int loop=1;loop<=cases;loop++)
    {
        scanf("%d",&n);
        flag=true;
        for (int i=1;i<=n;i++)
            point[i].code=i;
        for (int i=1;i<=n;i++)
            scanf("%d",&point[i].deg);
        memset(matrix,0,sizeof(matrix));
        for (int turn=1;turn<n;turn++)
        {
            qsort(point+turn,n-turn+1,sizeof(point_type),compare);
            //test();
            if (turn+point[turn].deg>n)
            {
                flag=false;
                break;
            }
            for (int i=turn+1;i<=turn+point[turn].deg;i++)
            {
                matrix[point[turn].code][point[i].code]=
                matrix[point[i].code][point[turn].code]=1;
                point[i].deg--;
                if (point[i].deg<0)
                    flag=false;
            }
            if (!flag)
                break;
        }
        if (flag&&(point[n].deg==0))
        {
            printf("YES\n");
            for (int i=1;i<=n;i++)
                for (int j=1;j<=n;j++)
                    printf("%d%c",matrix[i][j],j==n?'\n':' ');
        }
        else
            printf("NO\n");
        if (loop!=cases)
            printf("\n");
    }
    return 0;
}