【0】README
0.1)本文总结于 数据结构与算法分析, 旨在复习数据结构中图论算法的基础知识;
【1】图论若干相关定义
1.1)图G定义:一个图G=(V,E)由顶点及集V 和 边集E组成, 每一条边就是一个点对(v, w);
1.2)边邻接:当且仅当(v,w)∈E, 在无向图中, w和v邻接,且v也和w邻接;(还有第3中成分:边的权值)
1.3)路径: 一条路径是一个顶点序列 w1, w2,…,wn, 使得(wi,wi+1)∈E,这样一条路径长是该路径上的边数;
1.4)简单路径:其上的所有顶点都是互异的,但第一个顶点和最后一个顶点可能相同;
1.5)连通图(对于无向图而言): 如果在一个无向图中从每一个顶点到每个其他顶点都存在一条路径,则称该无向图是连通的;
1.6)强连通图(对于有向图而言):具有无向图连通性质的有向图称为是强连通的;
1.7)基础图:去掉有向图上的方向所形成的图;
1.8)弱连通图:如果有向图不是强连通的, 但基础图是连通的, 那么该图称为是弱连通的;
1.9)完全图: 是指每一对顶点间都存在一条边的图;
【2】图的表示
2.1)邻接矩阵:对于每条边(u, v), 我们设置 A[u][v]=1,否则数组的元素为0;如果边是有权的,设置A[u][v] 等于该权值 且用一个很大或者很小的权作为标记表示不存在的边;(∞)
- 2.1.1)邻接表的空间需求是 Θ(|V|^2);如果图是稠密的:|E| = Θ(|V|^2) , 则邻接矩阵是合适的表示方法;如果在大部分应用中,图都是稀疏的;
2.2)邻接表(图的标准表示方法):如果图是稀疏的, 则使用邻接表来表示。对每一个顶点,我们使用一个表存放所有邻接的顶点。此时的空间需求为 O(|E| + |V|);
- 2.2.1)引入散列表:在应用中,顶点都是名字而不是数字, 这些名字在编译时是未知的。由于我们不能够通过未知名字为一个数组做索引, 因此我们必须提供从名字到数字的映射。完成这项工作最容易的 方法是使用散列表, 在该散列表中我们对每个顶点存储一个名字以及一个范围在1到 |V| 之间的内部编号;
- 2.2.2)邻接表的一个荔枝:
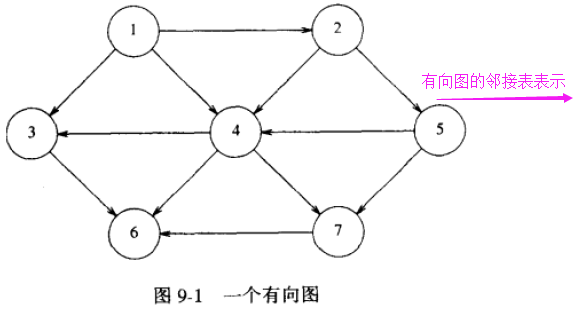 | 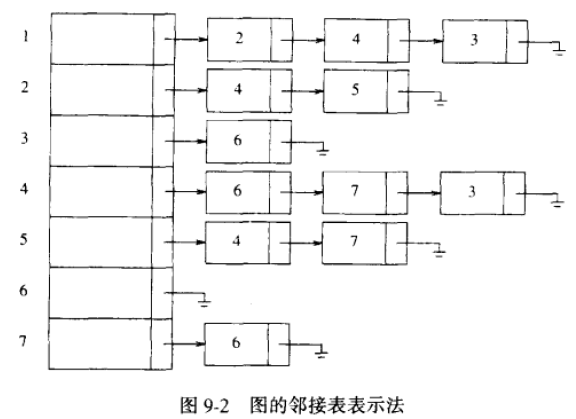 |





















 168万+
168万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








