ReviewForJob——最小生成树（prim + kruskal）源码实现和分析

【0】README

1）本文旨在给出 ReviewForJob——最小生成树（prim + kruskal）源码实现和分析， 还会对其用到的 技术 做介绍；

2）最小生成树是对无向图而言的：一个无向图G 的最小生成树是一个连通图，且保证该连通图 所含边的权值和最小；

3）要知道 Prim算法（普利姆算法）的基本 idea 就是 迪杰斯特拉算法，下面会介绍，所以我会po 出 迪杰斯特拉算法的 相关介绍；

4）下面的内容（参见迪杰斯特拉算法）转自 http://blog.csdn.net/pacosonswjtu/article/details/52125636 ：其实，说白了：广度优先搜索算法（计算无权最短路径） 是基于 拓扑排序算法的，而 迪杰斯特拉算法（计算有权最短路径） 是基于 广度优先搜索算法或者说是它的变体算法；上述三者不同点在于： 拓扑排序算法 和 广度优先搜索算法 使用了 循环队列， 而迪杰斯特拉算法使用了 二叉堆优先队列作为其各自的工具；相同点在于：他们都使用了 邻接表来表示图；所以 普利姆算法 也是基于 广度优先搜索算法的，且要使用二叉堆优先队列用于选取 权值最小的边；

5）需要事先知道的是：寻找最小生成树有两种alg—— 普利姆算法 和 克鲁斯卡尔算法，普利姆算法过程中有且只有一个连通图，而克鲁斯卡尔算法过程中 会形成多个 连通图；且 克鲁斯卡尔算法使用到了路径压缩，提高了find() 操作的效率，文末会讲到；

【1】Prim算法（普利姆算法） prim alg 源码

1）intro：普利姆算法用于在 无向图中寻找 最小生成树，其基本idea 同 迪杰斯特拉算法，上面已经提及过了；

2）与迪杰斯特拉算法不同的地方在于： 权值更新操作，废话不多说，上代码；

补充）普利姆算法的结束标志：当 所有顶点的状态都是已知（known==1）的时候，算法结束；

// 所有点相连的边的权值最小.
// adj:邻接表（图的标准表示方法）, table: 计算无权最短路径的配置表，heap：用于选取最小权值的邻接顶点的小根堆.
void prim(AdjList adj, UnWeightedTable table, int startVertex, BinaryHeap heap)
{		
	int capacity=adj->capacity;
	Vertex* arrayVertex = adj->array;
	Vertex temp;
	Entry* arrayEntry = table->array;
	int index; // 顶点标识符(从0开始取)
	int adjVertex;
	struct HeapNode node;
	int weight;
	int i=0; // 记录已知顶点个数（ known == 1 的 个数）.

	//step1(初始状态): startVertex 顶点插入堆. startVertex 从1 开始取.
	node.vertex=startVertex-1; // 插入堆的 node.vertex 从 0 开始取，所以startVertex-1.
	node.weight=0;
	insert(heap, node); // 插入堆.
	arrayEntry[startVertex-1]->dv=0;
	arrayEntry[startVertex-1]->pv=0;
	// 初始状态over.

	// step2: 堆不为空，执行 deleteMin操作. 并将被删除顶点的邻接顶点插入堆.
	while(!isEmpty(heap))
	{		
		if(i == capacity) // 当所有 顶点都 设置为 已知（known）时，退出循环.  
        {  
            break;  
        }  
		index = deleteMin(heap).vertex;  // index表示邻接表下标，从0开始取，参见插入堆的操作.
		arrayEntry[index]->known=1; // 从堆取出后，将其 known 设置为1.
		i++; // 记录已知顶点个数（ known == 1 的 个数）.

		temp = arrayVertex[index];		
		while(temp->next) 
		{
			adjVertex = temp->next->index; // 顶点index 的邻接节点标识符adjVertex 从1开始取.
			weight = temp->next->weight; // 顶点index到其邻接顶点 的权值.

			if(arrayEntry[adjVertex-1]->known == 0) // 注意: 下标是adjVertex-1, 且known==0 表明 adjVertex顶点还处于未知状态,所以adjVertex插入堆.
			{
				// prim 算法的代码版本.
				if(arrayEntry[adjVertex-1]->dv > weight ) // [key code] 当当前权值和 比 之前权值和 小的时候 才更新，否则不更新.
				{
					node.vertex=adjVertex-1; // 插入堆的 node.vertex 从 0 开始取.
					node.weight=weight;
					insert(heap, node); // 插入堆.
					arrayEntry[adjVertex-1]->dv = weight; // [also key code]					
					arrayEntry[adjVertex-1]->pv=index+1; // index 从0开始取，所以index加1.	
				}
				
				/* dijkstra 算法的代码版本.
				if(arrayEntry[adjVertex-1]->dv > arrayEntry[index]->dv + weight ) // [key code] 当当前权值和 比 之前权值和 小的时候 才更新，否则不更新.
				{
					node.vertex=adjVertex-1; // 插入堆的 node.vertex 从 0 开始取.
					node.weight=weight;
					insert(heap, node); // 插入堆.
					arrayEntry[adjVertex-1]->dv = arrayEntry[index]->dv + weight; // [also key code]					
					arrayEntry[adjVertex-1]->pv=index+1; // index 从0开始取，所以index加1.	
				}*/
			}			
			temp = temp->next;
		}
		  //printWeightedtable(table, 1);  // 取消这行注释可以 follow 迪杰斯特拉 alg 的运行过程.
	}	
} 

对权值更新的分析（Analysis）：

A1）普利姆算法的权值更新： 新权值== 其前驱顶点->该顶点的权值（weight）；

A2）迪杰斯特拉算法的权值更新：新权值== 其前驱的前驱顶点-> 前驱的权值（arrayEntry[index]->dv） + weight；

【2】Kruskal 算法（克鲁斯卡尔算法）克鲁斯卡尔源码

1）intro：连续地按照最小的权选择边，并且当所选的边不产生圈时就把它作为取定的边；

2）克鲁斯卡尔算法由多个连通图：将多个连通图进行合并，最终只有1个连通图，当添加到 连通图的边足够多时书法终止（如 顶点数目为7， 则当添加的边数为6 则算法终止）；事实上，克鲁斯卡尔算法就是要决定边 应该添加还是应该放弃；

3）克鲁斯卡尔算法用到的技术：

tech1）二叉堆优先队列：用于选取权值最小的边（deleteMin（binaryHeap）操作来完成）；

tech2）克鲁斯卡尔算法就是要决定边 应该添加还是应该放弃，这里用到了不相交集 ADT 的union/find 操作，当find(v1) 返回的集合标识 和 find(v2) 返回的集合标识不同时，则添加边(v1,v2)；否则放弃添加；

// 克鲁斯卡尔算法 用于寻找 最小生成树.
// 为什么这里没有把 邻接表作为参数传进来，因为即使将其作为参数，其还是要转化为 堆，
// 所以，为了算法的简洁性，在调用 kruskal() 方法前 就将 邻接表转化为 二叉堆优先队列了.
void kruskal(BinaryHeap heap, int* setArray, Edge* edgeSet, int edgeNum)  // 当顶点数=7时，edgeNum=6 因为 7个顶点最多6条边.
{
	int i=0;
	Edge edge;
	int set1, set2;

	while(!isEmpty(heap) && i<edgeNum)
	{
		edge = deleteMin(heap); // edge 不可能为空，因为heap 不为空（while循环）。
		set1 = find(setArray, edge->v1);
		set2 = find(setArray, edge->v2);

		// 克鲁斯卡尔算法就是要决定边 应该添加还是应该放弃
		if(set1 != set2) // 如果 v1 和 v2 不属于同一个集合，边就进行合并.
		{
			// setUnion begins.
			edgeSet[i++] = edge; // 添加边.			
			setArray[set2] = set1; //更新 edge->v2 的根的 集合标识. 而不能写成setArray[edge->v2] = set1;
			// setUnion over.
		}
	}
}	

tech3）为了提高find() 操作的效率，使用到了 路径压缩。为什么需要路径压缩？ 因为集合合并涉及两个操作：find 和 merge/setUnion 操作，又 find() 操作的执行效率取决于 树的高度，所以要进行路径压缩，减少树的高度（路径长度）（补充：路径压缩定义——设操作是 find(x)，此时路径压缩的效果是 从 x 到 根的路径上的每一个节点（包括x，但不包括根）都作为根的直接儿子） 路径压缩基础参见 路径压缩基础知识

// 寻找 index标识的 顶点 所在的集合.
// find() 涉及到路径压缩，路径压缩 基于 栈来实现（先进后出）.
int find(int* setArray, int index)
{
	int temp = index;
	int i=0;			
			
	while(index != setArray[index])
	{
		stack[i++] = index; // index 从 1 开始取，stack 的元素 也从 1 开始取.
		index = setArray[index]; // setArray 下标从1 开始.
	}	
		
	// 下面进行路径压缩(基于栈的观点). 
	while(--i >= 0)
	{
		setArray[ stack[i] ] = index;
	}	

	return index;
} 

对以上代码的分析（Analysis）：路径压缩是基于 不相交集 find 和 setUnion 操作，下面对其做分析

A1）起初，所有顶点都是一个集合，每个集合中只有一个顶点，有多少个顶点就有多少个集合，即setArray[i] = i（要知道0号下标不用的，这样为了编程方便），setArray[i] 中保存的是 仅仅是集合的标志；

A2）对边 执行 setUnion() 即合并之前，要执行find() 操作，查看 边的两个顶点 是否属于同一个集合，好比 v1-weight-v2 == edge 这条边， setArray[v1] == setArray[v2]? 如果它们返回的集合标识符相等，则放弃合并；否则将它们进行合并；

A3）合并也要分两个步骤： step1）将边添加到 edgeSet 集合中；step2）更新 任意一个顶点的根的集合 而不是 一个顶点的集合，这里是很重要的 ；什么叫做根？ 但 setArray[i] == i 的时候，我们认为 i标识所在的顶点叫做根；

看个合并荔枝）说了这么多，还不如一个荔枝来的快：再次提醒 当 setArray[i]==i 的时候，i标识的顶点才是根，才是集合的根，或是集合的标识；

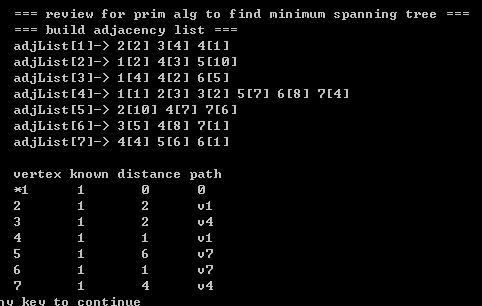
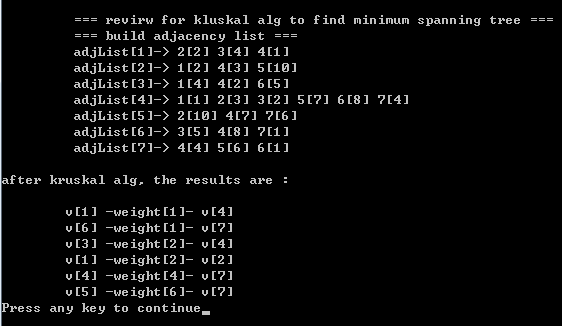
看个荔枝）什么叫路径压缩？在源码实现的测试用例中，通过堆的deleteMin 依次选择权值最小的边并添加到 edgeSet中，参考上述调试结果，我们知道选择顺序是 (v1, v4) (v6, v7) (v3, v4)(v1, v2)  (v2, v4) (v1,v3) (v4, v7) (v3, v6) (v5, v7)；

下面我们依次来分析 什么叫做路径压缩：

step1）(v1,v4) 被添加后，setArray[4]=1,又 setArray[1]=1（满足根的定义），所以v4 和v1 一样属于集合1；

step2）(v6, v7)被添加后，setArray[7]=6, 又 setArray[6]=6（满足根的定义），所以 v7 和 v6 一样属于集合6；

step3）(v3, v4) 被添加后，setArray[4]=1，setArray[1]=3, setArray[3]=3；因为 顶点4的根是顶点1，所以其根要和顶点3 属于同一个集合，则setArray[1]=3，下次find(4) 的路径为 setArray[4]=1 -> setArray[1]=3 -> setArray[3]=3（满足根的定义，over）

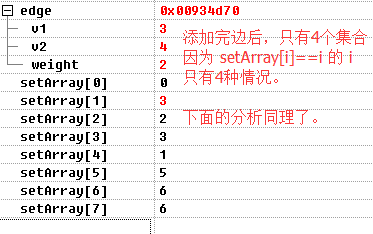
step4）(v1, v2)被添加后，setArray[2]=3，因为顶点3是顶点1 的 根；

step5）(v2,v4) v2 和 v4 属于同一集合，放弃添加；但是我们发现 setArray[4]=3 了，之前setArray[4]=1的，看看之前的结构是 根3->1->4， 再看看之后的结构是 根3->4 , 根3->1，这就是路径压缩的一个荔枝，因为顶点4 离根3 近了，这就提高了 find的查找效率，以前find(4) 的路径为2，现在的路径为1 因为直接就找到 顶点4的根3了；再次提醒，有兴趣的同学可以参考 路径压缩基础知识