14-在DX中建立第一人称相机

本章中，我们设计了一套与你在第一人称游戏中使用的相机相同的系统。该相机系统将会取代我们之前使用的轨道相机系统。

学习目标：
1.复习视图空间转换的数学原理。
2.能定义第一人称相机的典型功能。
3.学习如何实现第一人称相机。

14.1 视角变换复习

视图空间是连接到摄像机的坐标系，如图14.1所示。相机位于正视z轴的原点处，x轴指向相机右侧，y轴指向相机上方。相对于描述世界坐标下场景的顶点，渲染管线的后期阶段在相机坐标系下的描述更方便。从世界空间到视图空间的坐标变换称为视图变换，相应的矩阵称为视图变换矩阵。

如果$Q_w =(Q_x,Q_y,Q_z,1)，u_w =(u_x,u_y,u_z,0)，v_w =(v_x,v_y,v_z,0)，w_w =(w_x,w_y,w_z,0)$ ，分别描述相对于世界空间的摄像机空间齐次坐标的视图原点，x轴，y轴和z轴，那么从§3.4.3知道从视图空间到世界空间的变化矩阵是：

$$W= \left[ \begin{matrix} u_x&u_y&u_z&0 \\ v_x&v_y&v_z&0 \\ w_x&w_y&w_z&0\\ Q_x&Q_y&Q_z&1 \end{matrix} \right]$$
然而，这不是我们想要的转变。我们希望从世界空间到相机空间的变换。从§3.4.5中想到逆向变换可由求逆矩阵得出。因此 $W_{-1}$就是从世界空间到相机空间的变换。

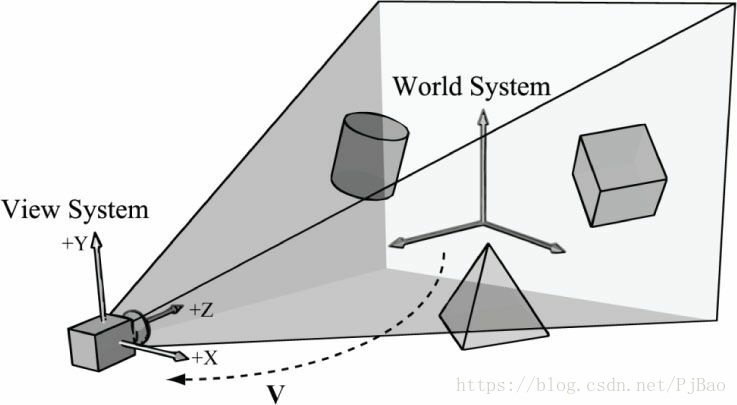图14.1 相机坐标系。 相对于它自己的坐标系，相机坐在原点向下看正z轴。
世界坐标系统和视图坐标系统一般只是位置和方向有所不同而已，因此直观地指出 $W=RT$（即，世界矩阵可以被分解为旋转，然后是平移）。这样使得求逆计算更容易：
$$V=W^{-1}=(RT)^{-1}=T^{-1}R^{-1}=T^{-1}R^T\\= \left[ \begin{matrix} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&1&0\\ Q_x&Q_y&Q_z&1 \end{matrix} \right] \left[ \begin{matrix} u_x&v_x&w_x&0 \\ u_y&v_y&w_y&0 \\ u_z&v_z&w_z&0\\ 0&0&0&1 \end{matrix} \right]= \left[ \begin{matrix} u_x&v_x&w_x&0 \\ u_y&v_y&w_y&0 \\ u_z&v_z&w_z&0\\ -Q_x·u&-Q_y·v&-Q_z·w&1 \end{matrix} \right]$$
所以视图矩阵如下：
$$V= \left[ \begin{matrix} u_x&v_x&w_x&0 \\ u_y&v_y&w_y&0 \\ u_z&v_z&w_z&0\\ -Q_x·u&-Q_y·v&-Q_z·w&1 \end{matrix} \right] \tag{eq. 14.1}$$
经过所有变换，我们没有移动场景中的任何东西。物体的位置变了是由于我们使用相机空间参照系代替了世界空间参考系。

14.2 Camera类

为了封装我们相机的相关代码，我们定义并实现了一个Camera类。Camera类的数据存储两个关键信息。摄像机的位置，右、上和观察观矢量分别定义了世界坐标系中视图空间坐标系统的原点，x轴，y轴和z轴，以及视锥体的属性。您可以将相机的镜头视为定义平截头体（其视场以及近平面和远平面）。很多方法并不重要（例如，简单的访问）。查看下面代码了解有关方法和数据成员的概述。我们会在下一节讲解一些重要方法。

class Camera
{
public:
    Camera();
    ~Camera();

    // Get/Set world camera position.
    XMVECTOR GetPositionXM()const;
    XMFLOAT3 GetPosition()const;
    void SetPosition(float x, float y, float z);
    void SetPosition(const XMFLOAT3& v);

    // Get camera basis vectors.
    XMVECTOR GetRightXM()const;
    XMFLOAT3 GetRight()const;
    XMVECTOR GetUpXM()const;
    XMFLOAT3 GetUp()const;
    XMVECTOR GetLookXM()const;
    XMFLOAT3 GetLook()const;

    // Get frustum properties.
    float GetNearZ()const;
    float GetFarZ()const;
    float GetAspect()const;
    float GetFovY()const;
    float GetFovX()const;

    // Get near and far plane dimensions in view space coordinates.
    float GetNearWindowWidth()const;
    float GetNearWindowHeight()const;
    float GetFarWindowWidth()const;
    float GetFarWindowHeight()const;

    // Set frustum.
    void SetLens(float fovY, float aspect, float zn, float zf);

    // Define camera space via LookAt parameters.
    void LookAt(FXMVECTOR pos, FXMVECTOR target, FXMVECTOR worldUp);
    void LookAt(const XMFLOAT3& pos, const XMFLOAT3& target,
    const XMFLOAT3& up);

    // Get View/Proj matrices.
    XMMATRIX View()const;
    XMMATRIX Proj()const;
    XMMATRIX ViewProj()const;

    // Strafe/Walk the camera a distance d.
    void Strafe(float d);
    void Walk(float d);

    // Rotate the camera.
    void Pitch(float angle);
    void RotateY(float angle);

    // After modifying camera position/orientation, call
    // to rebuild the view matrix once per frame.
    void UpdateViewMatrix();

private:
    // Camera coordinate system with coordinates relative to world space.
    XMFLOAT3 mPosition; // view space origin
    XMFLOAT3 mRight; // view space x-axis
    XMFLOAT3 mUp; // view space y-axis
    XMFLOAT3 mLook; // view space z-axis

    // Cache frustum properties.
    float mNearZ;
    float mFarZ;
    float mAspect;
    float mFovY;
    float mNearWindowHeight;
    float mFarWindowHeight;

    // Cache View/Proj matrices.
    XMFLOAT4X4 mView;
    XMFLOAT4X4 mProj;
};

注意：Camera.h/Camera.cpp文件位于Common目录中。

14.3 重要的方法及实施

许多相机类方法都是简单的 get/set方法，我们将在此省略。但是，我们将在本节中回顾一些重要的内容。

14.3.1 XMVECTOR返回变量

首先，我们要说的是，我们为许多“get”方法提供了XMVECTOR返回变量;这只是为了方便起见，以便客户端代码在需要XMVECTOR时不用转换：

XMVECTOR Camera::GetPositionXM()const
{
    return XMLoadFloat3(&mPosition);
}
XMFLOAT3 Camera::GetPosition()const
{
    return mPosition;
}

14.3.2 设置镜头

我们可以将这个视锥体看作我们的相机镜头，因为它控制着我们的视角。我们缓存平截头体属性并使用SetLens方法构建投影矩阵：

void Camera::SetLens(float fovY, float aspect, float zn, float zf)
{
    // cache properties
    mFovY = fovY;
    mAspect = aspect;

    mNearZ = zn;
    mFarZ = zf;

    mNearWindowHeight = 2.0f * mNearZ * tanf(0.5f*mFovY);
    mFarWindowHeight = 2.0f * mFarZ * tanf(0.5f*mFovY);

    XMMATRIX P = XMMatrixPerspectiveFovLH(mFovY, mAspect, mNearZ, mFarZ);
    XMStoreFloat4x4(&mProj, P);
}

14.3.3派生的Frustum信息

显而易见，我们缓存垂直视场角，并另外提供了一个计算水平视场角的方法。此外，我们提供方法来返回近平面和远平面上的平截头体的宽度和高度，这有时是有用的。这些方法的实现都是是三角函数，如果在推导方程时遇到问题，请查看§5.6.3：

float Camera::GetFovX()const
{
    float halfWidth = 0.5f*GetNearWindowWidth();
    return 2.0f*atan(halfWidth / mNearZ);
}

float Camera::GetNearWindowWidth()const
{
    return mAspect * mNearWindowHeight;
}

float Camera::GetNearWindowHeight()const
{
    return mNearWindowHeight;
}
float Camera::GetFarWindowWidth()const
{
    return mAspect * mFarWindowHeight;
}
float Camera::GetFarWindowHeight()const
{
    return mFarWindowHeight;
}

14.3.4 变换摄像机

对于第一人称相机，忽略碰撞检测，我们希望能够：
1.沿着其观察矢量前后移动相机。这可以通过沿其观察矢量平移相机位置来实现。
2.将相机沿着其右侧向量左右移动。这可以通过沿着其右矢量平移相机位置来实现。
3.将相机绕其右侧的矢量旋转以上下查看。这可以通过使用XMMatrixRotationAxis函数将相机的观察向量及上方向向量绕其右方向矢量旋转来实现。
4.围绕世界坐标的y轴（假设y轴对应于世界的“向上”方向）旋转摄像机以向右和向左看。这可以通过使用XMMatrixRotationY函数旋转所有基于世界y轴的矢量来实现。

void Camera::Walk(float d)
{
    // mPosition += d*mLook
    XMVECTOR s = XMVectorReplicate(d);
    XMVECTOR l = XMLoadFloat3(&mLook);
    XMVECTOR p = XMLoadFloat3(&mPosition);
    XMStoreFloat3(&mPosition, XMVectorMultiplyAdd(s, l, p));}
void Camera::Strafe(float d)
{
    // mPosition += d*mRight
    XMVECTOR s = XMVectorReplicate(d);
    XMVECTOR r = XMLoadFloat3(&mRight);
    XMVECTOR p = XMLoadFloat3(&mPosition);
    XMStoreFloat3(&mPosition, XMVectorMultiplyAdd(s, r, p));
}
void Camera::Pitch(float angle)
{
    // Rotate up and look vector about the right vector.
    XMMATRIX R = XMMatrixRotationAxis(XMLoadFloat3(&mRight), angle);
    XMStoreFloat3(&mUp, XMVector3TransformNormal(XMLoadFloat3(&mUp), R));
    XMStoreFloat3(&mLook, XMVector3TransformNormal(XMLoadFloat3(&mLook), R));
}
void Camera::RotateY(float angle)
{
    // Rotate the basis vectors about the world y-axis.
    XMMATRIX R = XMMatrixRotationY(angle);
    XMStoreFloat3(&mRight, XMVector3TransformNormal( XMLoadFloat3(&mRight), R));
    XMStoreFloat3(&mUp, XMVector3TransformNormal(XMLoadFloat3(&mUp), R));
    XMStoreFloat3(&mLook, XMVector3TransformNormal(XMLoadFloat3(&mLook), R));
}

14.3.5构建视图矩阵

第一部分中UpdateViewMatrix方法重新定义了摄像机的右、上和观察向量。也就是说，它确保它们为相互正交的单位向量。这很重要，因为经过几次旋转后，数值误差会累积并导致这些向量变为非正交。发生这种情况时，矢量不再表示直角坐标系，而是倾斜的坐标系，这不是我们希望的。该方法的第二部分只是将相机矢量插入公式14.1以计算视图变换矩阵。

void Camera:: UpdateViewMatrix()
{
    XMVECTOR R = XMLoadFloat3(&mRight);
    XMVECTOR U = XMLoadFloat3(&mUp);
    XMVECTOR L = XMLoadFloat3(&mLook);
    XMVECTOR P = XMLoadFloat3(&mPosition);

    //
    // Orthonormalize the right, up and look vectors.
    //

    // Make look vector unit length.
    L = XMVector3Normalize(L);

    // Compute a new corrected "up" vector and normalize it.
    U = XMVector3Normalize(XMVector3Cross(L, R));

    // Compute a new corrected "right" vector. U and L are
    // already ortho-normal, so no need to normalize cross product.
    // ||up × look|| = ||up|| ||look|| sin90° = 1
    R = XMVector3Cross(U, L);

    //
    // Fill in the view matrix entries.
    //
    float x = -XMVectorGetX(XMVector3Dot(P, R));
    float y = -XMVectorGetX(XMVector3Dot(P, U));
    float z = -XMVectorGetX(XMVector3Dot(P, L));

    XMStoreFloat3(&mRight, R);
    XMStoreFloat3(&mUp, U);
    XMStoreFloat3(&mLook, L);

    mView(0,0) = mRight.x;
    mView(1,0) = mRight.y;
    mView(2,0) = mRight.z;
    mView(3,0) = x;

    mView(0,1) = mUp.x;
    mView(1,1) = mUp.y;
    mView(2,1) = mUp.z;
    mView(3,1) = y;

    mView(0,2) = mLook.x;
    mView(1,2) = mLook.y;
    mView(2,2) = mLook.z;
    mView(3,2) = z;

    mView(0,3) = 0.0f;
    mView(1,3) = 0.0f;
    mView(2,3) = 0.0f;
    mView(3,3) = 1.0f;
}

14.4 相机演示程序讲解

现在我们可以删除应用程序类中与轨道相机系统相关的所有旧变量，例如mPhi，mTheta，mRadius，mView和mProj。我们将添加一个成员变量：

Camera mCam;

当窗口调整大小时，我们不再显式重建投影矩阵，而是使用SetLens将工作委托给Camera类：

void CameraApp::OnResize()
{
    D3DApp::OnResize();
    mCam.SetLens(0.25f*MathHelper::Pi, AspectRatio(), 1.0f, 1000.0f);
}

在UpdateScene方法中，我们处理键盘输入以移动相机：

void CameraApp::UpdateScene(float dt)
{
    //
    // Control the camera.
    //
    if(GetAsyncKeyState('W') & 0x8000)
        mCam.Walk(10.0f*dt);
    if(GetAsyncKeyState('S') & 0x8000)
        mCam.Walk(-10.0f*dt);
    if(GetAsyncKeyState('A') & 0x8000)
        mCam.Strafe(-10.0f*dt);
    if(GetAsyncKeyState('D') & 0x8000)
        mCam.Strafe(10.0f*dt);

在MouseMove方法中，我们旋转相机观看方向：

void CameraApp::OnMouseMove(WPARAM btnState, int x, int y)
{
    if((btnState & MK_LBUTTON) != 0)
    {
        // Make each pixel correspond to a quarter of a degree.
        float dx = XMConvertToRadians(0.25f*static_cast<float>(x - mLastMousePos.x));
        float dy = XMConvertToRadians(0.25f*static_cast<float>(y - mLastMousePos.y));
        mCam.Pitch(dy);
        mCam.RotateY(dx);
    }
    mLastMousePos.x = x;
    mLastMousePos.y = y;
}

最后，为了渲染，可以从相机实例访问视图矩阵和投影矩阵：

mCam.UpdateViewMatrix();
XMMATRIX view = mCam.View();
XMMATRIX proj = mCam.Proj();
XMMATRIX viewProj = mCam.ViewProj();

14.5 总结

1.我们通过指定相机坐标系的位置和方向来定义相机坐标系。位置由相对于世界坐标系的位置矢量指定，并且方位由相对于世界坐标系的三个正交矢量指定：右、上和观察矢量。移动相机相当于将相机坐标系相对于世界坐标系移动。

图14.2 相机演示的屏幕截图。 使用’W’，’S’，’A’和’D’键分别向前、向后、向左移动和向右移动。按住鼠标左键并移动鼠标以“观察”不同的方向
2.我们将投影相关量包括在相机类中，因为通过控制视场以及近平面和远平面，透视投影矩阵可以被认为是相机的“镜头”。
3.向前和向后移动可以简单地通过沿着其观察矢量平移摄像头位置来实现。只需将摄像头的位置沿着其右方向矢量平移，就可以实现右移和左移。通过将相机的观察向量和上方向矢量围绕其右方向向量旋转可以实现向上和向下的观看。通过旋转所有基于世界y轴的矢量来实现向左和向右看。

14.6 练习

1.给定世界坐标系中的世界空间轴和原点：$i=(1,0,0),j=(0,1,0),k=(0,0,1)$和$O=(0,0,0)$以及世界坐标系中的视图空间轴和原点：$u =(u_x,u_y,u_z),v=(v_x,v_y,v_z)，w =(w_x,w_y,w_z),Q=(Q_x,Q_y,Q_z)$，导出视图矩阵形式

$$V= \left[ \begin{matrix} u_x&v_x&w_x&0 \\ u_y&v_y&w_y&0 \\ u_z&v_z&w_z&0\\ -Q_x·u&-Q_y·v&-Q_z·w&1 \end{matrix} \right]$$
使用点积。 （记住，要找到坐标矩阵从世界空间到视图空间的变化，只需要用相对于视图空间的坐标来描述世界空间轴和原点，然后这些坐标变成视图矩阵的行）。

2.修改相机演示以支持“滚动”。这是相机围绕其外观矢量旋转的位置。 这可能对飞机游戏有用。