【生物医学信号处理及其MATLAB应用】Chapter 3 随机信号基础

3.1 随机信号

​ 信号可分为确定性信号和随机信号，所谓随机信号就是不能用一个确切的数学公式来描述，因而也不能准确地予以预测的信号，即随机信号只能用统计方法进行描述，只能在一定的准确性或可信性范围内进行预测。

​ 随机信号具有以下性质：

​ ①随机信号中的任何一个点上的取值都是不能先验确定的随机变量

​ ②随机信号可以用它的统计平均特征来表征

​ 随机信号的表示法有古典的统计法和现代的参数建模法

3.2 随机信号的统计特征描述

3.2.1 概率分布函数

1. 一维概率分布函数

​ 对于一个随机变量$x_n$，用$P_{x_n}(x_1,n)$来表示它的概率分布函数，则有：

​ $P_{x_n}(x_1,n)=$概率{$x_n\le x_1$}

​ 如果$x_n$的取值是离散的，则用$P_{x_n}(x_1,n)$来表示它的概率分布函数：

​ $P_{x_n}(x_1,n)=$概率[$x_n=x_1$]

​ 表示$x_n$取某一值$x_1$的概率。

2. 二维概率分布函数

​ 如果要描述一个随机过程中的两个时间点（$n_1$与$n_2$）上的随机变量$x_{n_1}$和$x_{n_2}$之间的关系，可以用二维联合概率分布函数来表示：

​ $P_{x_{n_1}{x}_{n_2}}(x_1,n_1;x_2,n_2)=$概率$(x_{n_1}\le x_1,x_{n_2}\le x_2)$

​ 它表示$x_{n_1}\le x_1$同时$x_{n_2}\le x_2$的联合概率。

​ 二维联合概率分布函数的二阶偏微分对应着相应的二维联合概率密度函数：

​ $P_{x_{n_1},x_{n_2}}(x_1,n_1;x_2,n_2)=$概率$(x_{n_1}=x_1,x_{n_2}=x_2)$

​ 它表示$x_{n_1}$取值$x_1$同时$x_{n_2}$取值$x_2$的联合概率。

​ 当随机变量$x_{n_1}$和$x_{n_2}$统计独立时，则有：

​ $P_{x_{n_1},x_{n_2}}=P_{x_{n_1}}(x_1,n_1)P_{x_{n_2}}(x_2,n_2)$

3.2.2 各态遍历随机过程

1. 平稳随机过程

​ 如果随机信号的概率特性不随时间变化而变化，则称为平稳随机过程，否则称为非平稳随机过程。

​ 一阶平稳过程（First Order Stable Process）：信号的平均值与$t$无关的过程叫做一阶平稳过程（$m=1$）。

​ 二阶（$m=2$）平稳过程（Second Order Stable Process）：①信号的平均值与$t$无关；②信号的均方值与$t$无关；③信号的协方差只是时间间隔的函数，而与时间原点的选择无关。

​ 如果该随机过程是一个高斯过程，则二阶平稳意味着完全平稳。

2. 各态遍历随机信号

​ 各态遍历随机信号（Ergodic Random Signal）是指所有样本函数在某给定时刻的统计特性与单一样本函数在长时间内的统计特性一致的平稳随机信号，即单一样本函数随时间变化的过程可以包括该信号所有样本函数的取值经历。

​ 随机信号的各态遍历特性（Ergodicity）使我们能由单一样本函数的时间平均来代替集总（Ensemble）平均，随机信号的平稳特性可使我们能从任意时间原点开始求取统计特征，使得在实际工作中，估计统计平均量成为可能。

3.3 几种典型的随机过程

1. 高斯（正态）过程

​ 描述过程特性的所有概率密度函数都是高斯型的，假设各时刻随机过程的取值组成的矢量是$[x_1,x_2,...,x_n]$，它的均值为$\mu =[m_1,m_2,...,m_n{]}^{{}^{\prime }}$，协方差矩阵为：

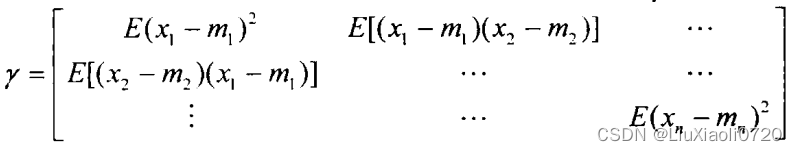
则它的概率密度函数为：

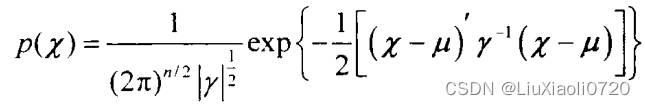
高斯过程具有以下特性：只要知道信号的均值矢量和协方差矩阵，则任意阶的概率密度函数都可以解析表达出。只要均值和方差是常数，则协方差只与时间差有关（即一、二阶平稳），即必然是高阶平稳。如果各随机变量互不相关，也必然互相独立。高斯过程经过线性运算（加、减、微分、积分）后还是高斯型的。

2. 理想白噪过程

​ 功率谱是常数的随机过程称为白噪过程。设白噪过程$w(n)$的功率谱为：

​ $P_w(e^{jw})=A$

​ 则其自相关函数为：

​ $$R_{ww}(m)=IDTFT[P_w(e^{jw})]=A\delta (m)$$

​ 只有当$m=0$时，自相关才有值，否则该值为零，即不同时刻白噪的取值总正交。

3. 限带白噪过程

​ 实际的线性系统总是有限的带宽，理想白噪通过线性系统后也会变成有限带宽。用$w(n)$表示限带白噪过程，该功率谱为：
​
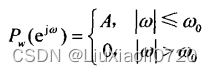
​ 则其自相关函数为：

​ $R_{ww}(m)=IDTFT[P_w{e}^{jw}]=A\frac{w_0}{\pi }\frac{sin{w}_{0}m}{w_{0}m}$

3.4 随机信号通过线性系统

​ 研究确定信号通过线性系统时常用的方法是傅里叶变换。当$x(n)$是随机信号时就无法求它的傅里叶变换，要想分析输出信号$y(n)$可以考虑分析$y$的概率密度函数，或者分析$y$的自相关函数或功率谱密度，反映二阶特性；或者分析$y$的均值、方差，反映一阶特性。

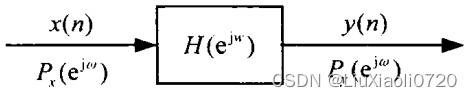
随机信号通过线性系统的基本关系式为：

​ ①$P_y(e^{jw})=|H(e^{jw}){|}^2{P}_x(e^{jw})$

​ ②$R_y(m)=R_x(m)\ast h(-m)\ast h(m)$

​ ③$P_{xy}(e^{jw})=H(e^{jw})P_x(e^{jw})$

​ ④$R_{xy}(m)=R_x(m)\ast h(m)$

​ 等式①②是一对DTFT，等式③④也是一对DTFT。

3.5 MATLAB应用

3.5.1 随机信号时域和频域认识

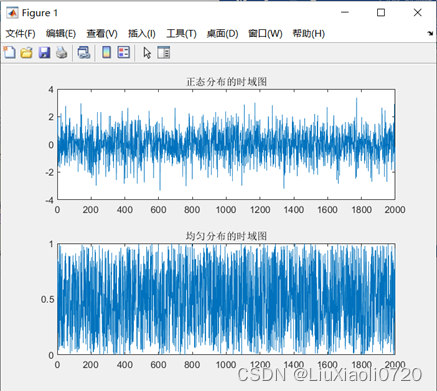
​ 1.在波形产生函数中选randn和rand两种波形发生器，各产生一段随机信号，请观察它们是什么样的信号，描述它们的时域特征。

​ 2.编制一个程序，计算这两个随机信号的样本数字特征，包括均值、方差、相关函数（xcorr）、协方差函数（xcov），比较并描述这两个信号一阶和二阶统计量的区别。

​ 3.对以上信号样本计算频数分布直方图（hist）并估计这两个随机信号的概率密度函数（ksdensity）及估计他们的概率分布函数（ksdensity）。

​ 4.利用周期图法估计这两个信号功率谱，比较并描述它们的频域特征。

​ 5.查看相关函数结果和功率谱之间是否是一对DFT。

clear;clc;close all;
% 产生两种随机信号
N = 2000;
x = randn(1, N);  % 正态分布
y = rand(1, N);  % 均匀分布
figure;
subplot(2, 1, 1);plot(x);
title('正态分布的时域图');
subplot(2, 1, 2);plot(y);
title('均匀分布的时域图');

% 求均值
xmean = mean(x)  % 正态分布的均值
ymean = mean(y)  % 均匀分布的均值
% 求方差
xvar = var(x)  % 正态分布的方差
yvar = var(y)  % 均匀分布的方差
% 画直方图
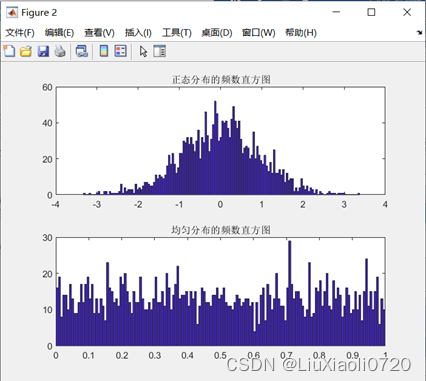
figure;
subplot(2, 1, 1);hist(x, 150);
title('正态分布的频数直方图');
subplot(2, 1, 2);hist(y, 150);
title('均匀分布的频数直方图');
% 画自相关
% 随机信号是非周期信号，此处更适合使用有偏方式计算
[x_xcorr, x_lag] = xcorr(x, 'biased');  % 有偏，x自相关
[y_xcorr, y_lag] = xcorr(y, 'biased');  % 有偏，y自相关
figure;
subplot(2, 1, 1);plot(x_lag, x_xcorr);  % R=E[x(n)x(n+m)]，m=0时理论值R=1，m≠0时理论值R=0
title('正态分布的自相关函数');
subplot(2, 1, 2);plot(y_lag, y_xcorr);  % R=E[xn.^2]=σ.^2+m.^2，m=0时理论值R=1/3，m≠0存在直流成分
title('均匀分布的自相关函数');
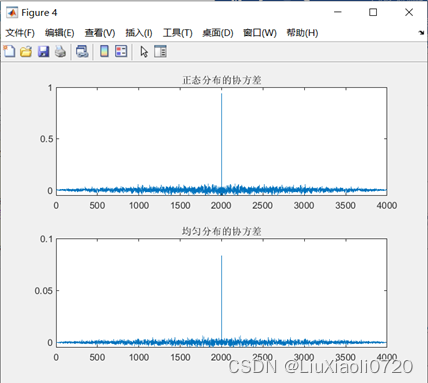
% 画协方差
% 在相关函数的基础上减掉均值成分
x_xcov = xcov(x, 'biased');  % 有偏
y_xcov = xcov(y, 'biased');  % 有偏
figure;
subplot(2, 1, 1);plot(x_xcov);
title('正态分布的协方差');
subplot(2, 1, 2);plot(y_xcov);
title('均匀分布的协方差');
% 画概率密度函数
[f1, xgm] = ksdensity(x);
[f2, ygm] = ksdensity(y);
figure;
subplot(2, 1, 1);plot(xgm, f1);
title('正态分布的概率密度函数');
subplot(2, 1, 2);plot(ygm, f2);
title('均匀分布的概率密度函数');
%% 画概率分布函数
%% 对概率密度函数求积分
% h1 = n1/1000/f1;
% fb1 = cumsum(h1*f1);
% figure;
% subplot(2, 1, 1);
% plot(x1, fb1);title('正态分布的概率分布函数');
% subplot(2, 1, 2);
% plot(x2, fb2);title('均匀分布的概率分布函数');

%% ksdensity求概率分布函数
% [f11, xgm1] = ksdensity(x, 'function', 'cdf');
% [f22, ygm2] = ksdensity(y, 'function', 'cdf');
% figure;
% subplot(2, 1, 1);plot(xgm1, f11);
% title('正态分布的概率分布函数');
% subplot(2, 1, 2);plot(ygm2, f22);
% title('均匀分布的概率分布函数');

%% cdfplot
figure;
subplot(2, 1, 1);
cdfplot(x);title('正态分布的概率分布函数');
subplot(2, 1, 2);
cdfplot(y);title('均匀分布的概率分布函数');

%% 功率谱
% 周期图法估计这两个信号的功率谱
fs = N;
nfft = 1024;
x_xcorr_fft = fft(x_xcorr);
y_xcorr_fft = fft(y_xcorr);
pxx = abs(x_xcorr_fft);
pyy = abs(y_xcorr_fft);
figure;
subplot(2, 2, 1);
plot(10*log10(pxx));
title('相关函数求功率谱：正态分布x');
subplot(2, 2, 2);
plot(10*log10(pyy));
title('相关函数求功率谱：均匀分布y');

px = abs(fft(x, 2*N - 1)).^2/N;
py = abs(fft(y, 2*N - 1)).^2/N;
subplot(2, 2, 3);
plot(10*log10(px));
title('周期图法求功率谱：正态分布x');
subplot(2, 2, 4);
plot(10*log10(py));
title('周期图法求功率谱：均匀分布y');

运行结果：

​ $rand$生成均匀分布在$0-1$之间的伪随机数，而$randn(m,n)$生成$m$行$n$列标准正态分布的伪随机数（均值为$0$，方差为$1$）。从图中和均值和方差的计算结果可以看出，均匀分布信号方差较小，均值接近$0.5$，正态分布信号均值接近$0$，方差接近$1$。


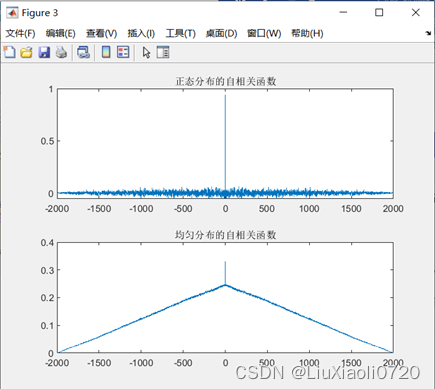
由于选取的两个随机信号均为非周期信号，所以此处更适合使用有偏方式进行计算。从图4和图5可以看出，均匀分布信号的自相关函数在中点时最大，离中点越远越小（逐渐减小），这是因为均匀分布的自相关$R=E[x_n^2]={\sigma }^2+m^2$，$m=0$时理论值$R=\frac{1}{3}$，$m\ne 0$时存在直流成分，正态分布信号的自相关函数和自协方差在$0$处有一个尖峰，其他位置都近似于$0$，这是因为正态分布的自相关$R=E[x(n)x(n+m)]$，$m=0$时理论值$R=1$，$m\ne 0$时理论值$R=0$，自协方差与自相关的关系为$C_{xx}(m)=R_{xx}(m)-m_x^2$，在自相关基础上减去均值，因此正态分布的协方差与自相关呈现相似的变化趋势，而均匀分布的自协方差是在自相关基础上减去均值，因此计算所得的自协方差在中点时最大，其他位置近似于$0$。


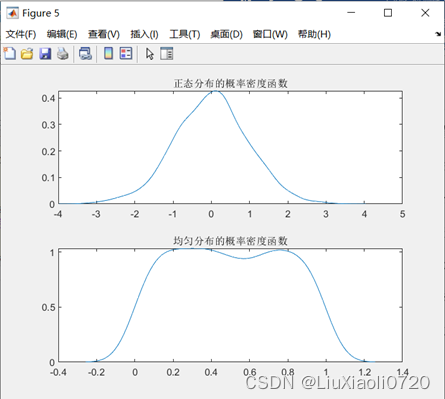
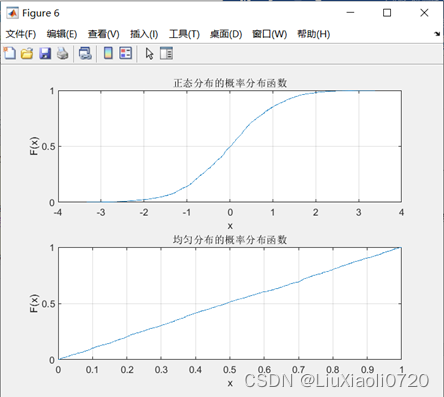
从图6和图7中可以看出，$rand$信号的概率密度近似均匀分布在$0-1$之间，概率分布函数近似为线性函数，而$randn$信号近似成均值为$0$的正态分布。

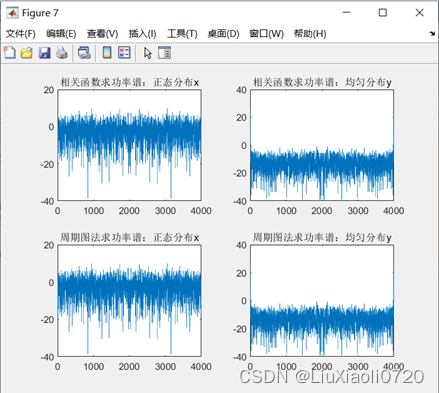
从图8可以看出，均匀分布信号功率谱在低频段比较集中，而正态分布信号功率谱近似均匀地分布在各个频段。从上图中也可以观察到，在忽略数值计算误差的前提下，利用相关函数计算得到的功率谱与通过周期图法求解的功率谱结果近似相等，而利用相关函数计算功率谱则需要先对信号的相关函数，再求其傅里叶变换，因此可以证明相关函数和功率谱是一对DFT。

​ 该条结论由维纳和辛钦先后发现，称为维纳—辛钦定理，该定理指出：任意一个均值为常数的广义平稳随机过程的功率谱密度是其自相关函数的傅立叶变换。

3.5.2 开闭眼脑电信号特征的认识

​ 1.选择一路脑电信号，观察和描述开眼和闭眼脑电信号的时域波形特征。

​ 2.使用周期图法对开眼和闭眼的脑电信号进行分析，探讨不同窗函数对分析结果的影响。

​ 3.将某一种窗函数下的开眼和闭眼功率谱图进行比较，找出开眼与闭眼功率谱上存在的差异。

clear;clc;
fs = 250;
t = 0:1/fs:1;
N = length(t) - 1;
w = 0:fs/N:fs;
nfft = 1024;
load('eegopen.mat');
load('eegclose.mat');
x = eegopen(:, 8);  % 睁眼脑电数据
y = eegclose(:, 8);  % 闭眼脑电数据

figure;
subplot(2, 1, 1);
plot(x);
ylabel('幅度/uv');title('睁眼脑电波');
subplot(2, 1, 2);
plot(y);
ylabel('幅度/uv');title('闭眼脑电波');

% 求均值
xmean = mean(x)
ymean = mean(y)
% 求方差
xvar = (std(x))^2
yvar = (std(y))^2
% 画直方图
figure;
subplot(2, 1, 1);hist(x, 150);
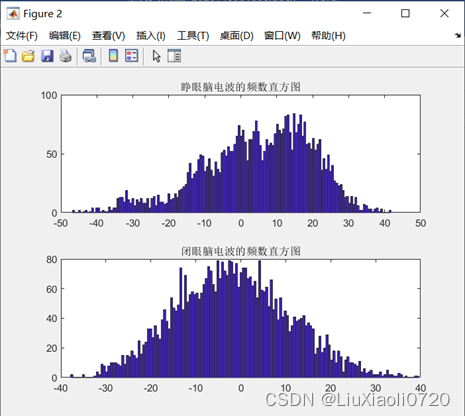
title('睁眼脑电波的频数直方图');
subplot(2, 1, 2);hist(y, 150);
title('闭眼脑电波的频数直方图');
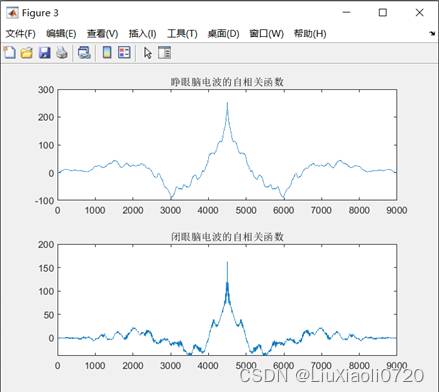
% 画相关函数
x_xcorr = xcorr(x, 'unbiased');
y_xcorr = xcorr(y, 'unbiased');
figure;
subplot(2, 1, 1);
plot(x_xcorr);title('睁眼脑电波的自相关函数');
subplot(2, 1, 2);
plot(y_xcorr);title('闭眼脑电波的自相关函数');
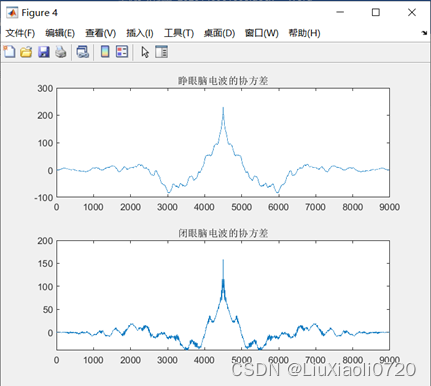
% 画协方差
x_xcov = xcov(x, 'unbiased');  
y_xcov = xcov(y, 'unbiased'); 
figure;
subplot(2, 1, 1);plot(x_xcov);
title('睁眼脑电波的协方差');
subplot(2, 1, 2);plot(y_xcov);
title('闭眼脑电波的协方差');
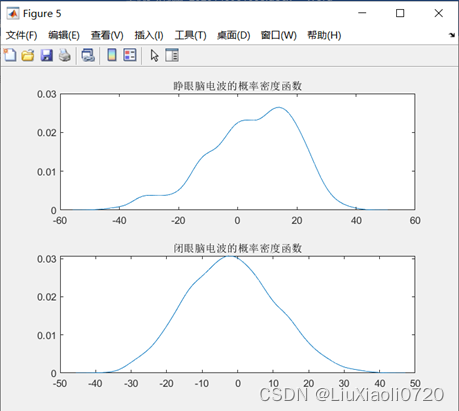
% 画概率密度函数
[f1, xgm] = ksdensity(x);
[f2, ygm] = ksdensity(y);
figure;
subplot(2, 1, 1);
plot(xgm, f1);title('睁眼脑电波的概率密度函数');
subplot(2, 1, 2);
plot(ygm, f2);title('闭眼脑电波的概率密度函数');

% delta波1~3Hz，theta波4~7Hz，alpha波8~13Hz，beta波14~30Hz
% 构造三角窗，周期图法求功率谱
x_sanjiao = triang(length(x));
y_sanjiao = triang(length(y));
[px1, fx1] = spectrogram(x, x_sanjiao);
[py1, fy1] = spectrogram(y, y_sanjiao);
fx1 = fx1*250/(2*pi);
fy1 = fy1*250/(2*pi);
figure;
subplot(2, 1, 1);
plot(fx1, 10*log10(px1));
title('三角窗求功率谱：x');
ylabel('以10log10为底');
subplot(2, 1, 2);
plot(fy1, 10*log10(py1));
title('三角窗求功率谱：y');
ylabel('以10log10为底');
% 构造汉明窗
x_hanming = hamming(length(x));
y_hanming = hamming(length(y));
[px2, fx2] = spectrogram(x, x_hanming);
[py2, fy2] = spectrogram(y, y_hanming);
fx2 = fx2*250/(2*pi);
fy2 = fy2*250/(2*pi);
figure;
subplot(2, 1, 1);
plot(fx2, 10*log10(px2));
title('汉明窗求功率谱：x');
ylabel('以10log10为底');
subplot(2, 1, 2);
plot(fy2, 10*log10(py2));
title('汉明窗求功率谱：y');
ylabel('以10log10为底');
% 构造凯撒窗
x_kaisa = kaiser(length(x));
y_kaisa = kaiser(length(y));
[px3, fx3] = spectrogram(x, x_kaisa);
[py3, fy3] = spectrogram(y, y_kaisa);
fx3 = fx3*250/(2*pi);
fy3 = fy3*250/(2*pi);
figure;
subplot(2, 1, 1);
plot(fx3, 10*log10(px3));
title('凯撒窗求功率谱：x');
ylabel('以10log10为底');
subplot(2, 1, 2);
plot(fy3, 10*log10(py3));
title('凯撒窗求功率谱：y');
ylabel('以10log10为底');

% 求睁眼脑电各波段峰值
% aa = 10*log10(px2);
a1 = max(10*log10(px2(find(fx2>=1 & fx2<=3))))
a2 = max(10*log10(px2(find(fx2>=4 & fx2<=7))))
a3 = max(10*log10(px2(find(fx2>=8 & fx2<=13))))
a4 = max(10*log10(px2(find(fx2>=14 & fx2<=30))))

% 求闭眼脑电各波段数据
% bb = 10*log10(py2);
b1 = max(10*log10(py2(find(fy2>=1 & fy2<=3))))
b2 = max(10*log10(py2(find(fy2>=4 & fy2<=7))))
b3 = max(10*log10(py2(find(fy2>=8 & fy2<=13))))
b4 = max(10*log10(py2(find(fy2>=14 & fy2<=30))))

运行结果：


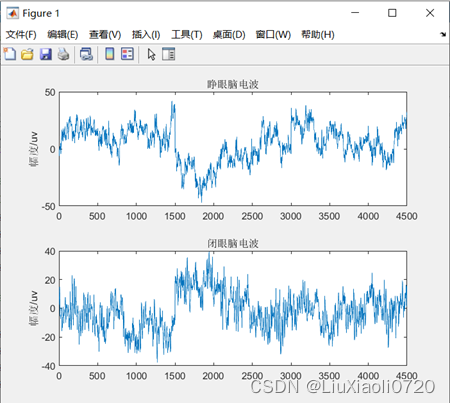
观察图2可以发现，睁闭眼脑电在1500~2500s区域差异较明显，表现为睁眼脑电在该段的峰值低于闭眼脑电，且闭眼脑电整体频率高于睁眼脑电，可能与闭眼状态下$\alpha$波功率显著高于开眼，且两种状态下的脑区活动差异显著有关。








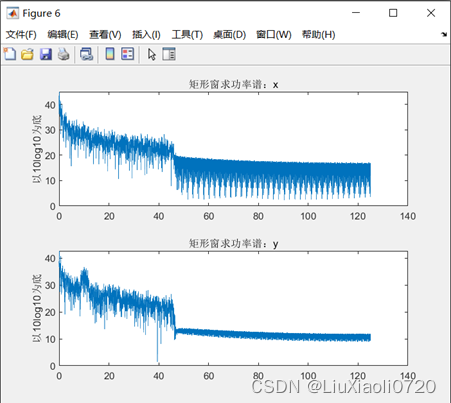
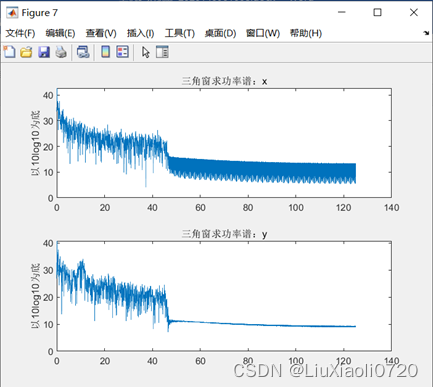
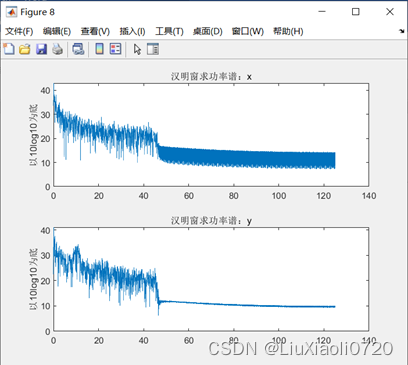
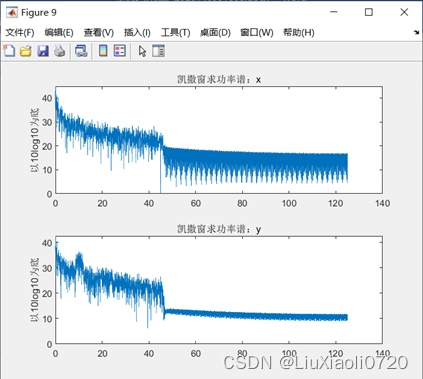
选取窗函数的长度$N=length(x)$（或$N=length(y)$），通过对比可以发现，矩形窗的功率谱分析效果较差（矩形窗的作用相当于截断信号），汉明窗比加矩形窗和三角窗更加平滑，而加凯撒窗的功率谱在高频段比较平滑，在低频段不平滑。以汉明窗分析为例，计算睁闭眼脑电在各频段的峰值：

	δ波1~3Hz峰值	θ波4~7Hz峰值	α波8~13Hz峰值	β波14~30Hz峰值
睁眼脑电	37.8776	32.2308	30.0532	28.2955
闭眼脑电	34.5550	30.4721	33.4719	28.8084

​ 对比取对数后的功率增益可以发现，闭眼状态下$\alpha$波功率显著高于睁眼状态，这可能是由于睁眼状态下，随着视觉信息的输入，与$\alpha$波功率相关的脑区活动减弱。

3.5.3 改进周期图法估计功率谱

​ 在3.5.2的基础上，任选一种窗函数，用分段、平均的思想改进周期图法，观察改进前后功率谱的差异。

clear;clc;
load('eegopen.mat');
load('eegclose.mat');
a = eegopen(:, 8);  % 睁眼数据，打开所选导联数据
b = eegclose(:, 8);  % 闭眼数据，打开所选导联数据
fs = 250;
figure;
plot(1:4500, a, 1:4500, b, 'r');axis([1, 4500, -100, 100]);
title('睁眼与闭眼的时域图对比');
legend('睁眼', '闭眼');

n = 4500;x = 1:4500;
recwin = boxcar(n);  % 构造矩形窗
triwin = triang(n);  % 构造三角窗
hamwin = hamming(n);  % 构造汉明窗
blackwin = blackman(n);  % 构造布莱克曼窗
kaize = kaiser(n);  % 构造凯撒窗

% 直接法
gl1 = abs(fft(a)).^2/length(b);
gl2 = abs(fft(b)).^2/length(b);
F1 = 0:2/length(gl1):2 - 1/length(gl1);
F2 = 0:2/length(gl2):2 - 1/length(gl2);
figure;
plot(F1, gl1, F2, gl2);axis([0 1 0 5000]);
title('睁闭眼直接法功率谱对比');
legend('睁眼', '闭眼');

% 加窗平滑法
power1 = abs(fft(a(1:n).*hamwin)).^2/n;
power2 = abs(fft(b(1:n).*hamwin)).^2/n;
F1 = 0:2/length(power1):2 - 1/length(power1);
F2 = 0:2/length(power2):2 - 1/length(power2);
figure;
plot(F1, power1, F2, power2, 'r');
axis([0 1 0 5000]);
title('睁闭眼加hamming窗功率谱对比');
legend('睁眼', '闭眼');

% 分段加窗平均法
% gl1 = [];gl2 = [];
L1 = 5;
w = 4500/L1;
a_hamwin = a(1:n).*hamwin;
b_hamwin = b(1:n).*hamwin;

fta11 = abs(fft(a_hamwin(1:w))).^2/n;
fta22 = abs(fft(a_hamwin(w+1:2*w))).^2/n;
fta33 = abs(fft(a_hamwin(2*w+1:3*w))).^2/n;
fta44 = abs(fft(a_hamwin(3*w+1:4*w))).^2/n;
fta55 = abs(fft(a_hamwin(4*w+1:5*w))).^2/n;
gl11 = (fta11 + fta22 + fta33 + fta44 + fta55)/5;

ftb11 = abs(fft(b_hamwin(1:w))).^2/n;
ftb22 = abs(fft(b_hamwin(w+1:2*w))).^2/n;
ftb33 = abs(fft(b_hamwin(2*w+1:3*w))).^2/n;
ftb44 = abs(fft(b_hamwin(3*w+1:4*w))).^2/n;
ftb55 = abs(fft(b_hamwin(4*w+1:5*w))).^2/n;
gl22 = (ftb11 + ftb22 + ftb33 + ftb44 + ftb55)/5;

F1 = 0:2/length(gl1):2 - 1/length(gl1);
F2 = 0:2/length(gl2):2 - 1/length(gl2);
figure;plot(F1, gl1, F2, gl2, 'r');
axis([0 1 0 2000]);
title('睁闭眼分5段加hamming窗平均法功率谱对比');
legend('睁眼', '闭眼');


L2 = 8;
w = 4500/L2;
a_ham = a(1:n).*hamwin;
b_ham = b(1:n).*hamwin;

fta11 = abs(fft(a_ham(1:w))).^2/n;
fta22 = abs(fft(a_ham(w+1:2*w))).^2/n;
fta33 = abs(fft(a_ham(2*w+1:3*w))).^2/n;
fta44 = abs(fft(a_ham(3*w+1:4*w))).^2/n;
fta55 = abs(fft(a_ham(4*w+1:5*w))).^2/n;
fta66 = abs(fft(a_ham(5*w+1:6*w))).^2/n;
fta77 = abs(fft(a_ham(6*w+1:7*w))).^2/n;
fta88 = abs(fft(a_ham(7*w+1:8*w))).^2/n;
gl111 = (fta11 + fta22 + fta33 + fta44 + fta55 + fta66 + fta77 + fta88)/8;

ftb11 = abs(fft(b_ham(1:w))).^2/n;
ftb22 = abs(fft(b_ham(w+1:2*w))).^2/n;
ftb33 = abs(fft(b_ham(2*w+1:3*w))).^2/n;
ftb44 = abs(fft(b_ham(3*w+1:4*w))).^2/n;
ftb55 = abs(fft(b_ham(4*w+1:5*w))).^2/n;
ftb66 = abs(fft(b_ham(5*w+1:6*w))).^2/n;
ftb77 = abs(fft(b_ham(6*w+1:7*w))).^2/n;
ftb88 = abs(fft(b_ham(7*w+1:8*w))).^2/n;
gl222 = (ftb11 + ftb22 + ftb33 + ftb44 + ftb55 + ftb66 + ftb77 + ftb88)/8;

F1 = 0:2/length(gl111):2 - 1/length(gl111);
F2 = 0:2/length(gl222):2 - 1/length(gl222);
figure;plot(F1, gl111, F2, gl222);
axis([0 0.5 0 400]);
title('睁闭眼分8段加hamming窗平均法功率谱对比');
legend('睁眼', '闭眼');

% welch法
[PHx1, F1] = pwelch(a, hamwin);
[PHx2, F2] = pwelch(b, hamwin);
figure;grid on;
F1 = 0:1/length(F1):1 - 1/length(F1);
F2 = 0:1/length(F2):1 - 1/length(F2);
plot(F1, PHx1, F2, PHx2, 'r');
axis([0 1 0 5000]);
title('睁闭眼welch法功率谱对比');
legend('睁眼', '闭眼');

% 计算方差（以睁眼信号为例）
a1_var = (std(gl1))^2  % 直接法
a2_var = (std(power1))^2  % 加窗平滑法（周期图法）
a3_var = (std(gl11))^2  % 分段加窗平滑法（平均周期图法，L=5）
a4_var = (std(gl111))^2  % 分段加窗平滑法（平均周期图法，L=8）
a5_var = (std(PHx1))^2  % welch法（改进的周期图法）

运行结果：

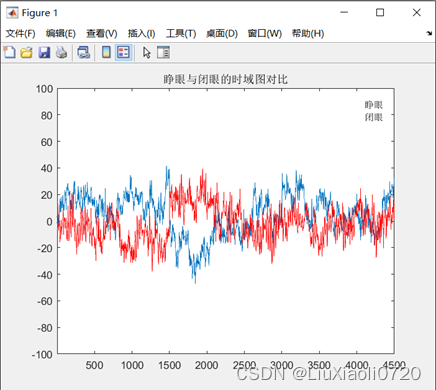
从时域图中观察到，睁眼和闭眼脑电的幅度分布在-40-40之间，在1500~2200段睁眼脑电的幅度比闭眼脑电的幅度略低，其他段睁眼脑电的幅度略高于闭眼脑电。





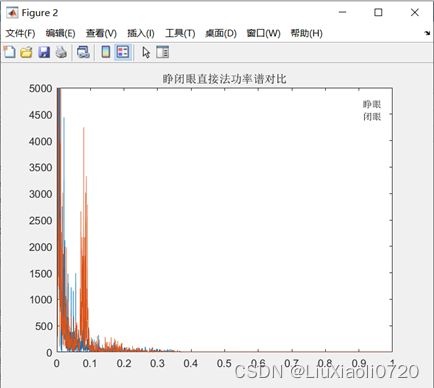
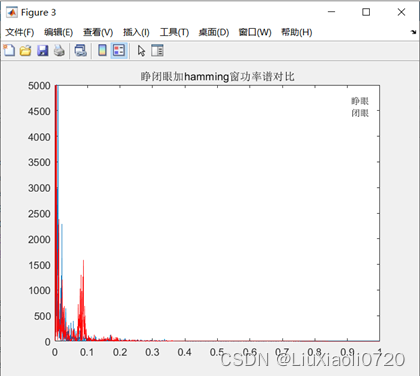
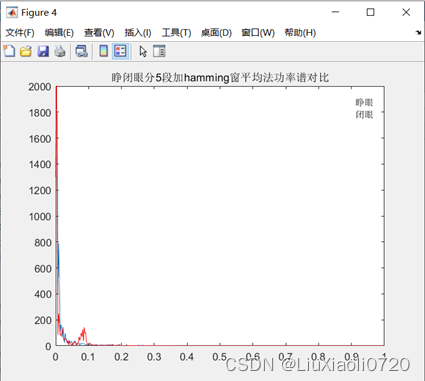
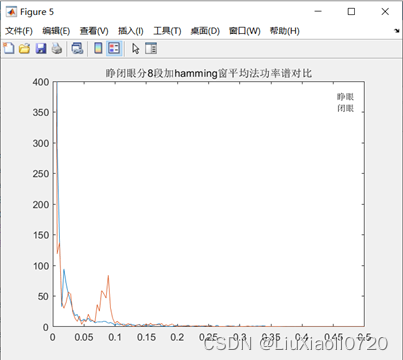
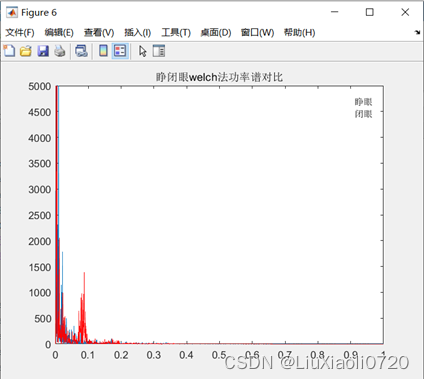
表1.方法对比

	直接法	周期图法	平均周期图法（分5段）	平均周期图法（分8段）	welch法
方差	1.7903e+07	4.5547e+06	6.1795e+04	2.9151e+04	2.9578e+06

​ 从图中可以看出，分段数为5时计算得到的功率谱比直接法和加窗平滑法计算得到的功率谱平滑，将分段数改为8后功率谱更加平滑，但是细节可见度也随之降低。

​ 理论分析可知，对$N$个离散的数据点$u_N(n)$，对这些数据点进行傅里叶变换，得到$U_N(w)={\sum }_{n=0}^{N-1}{u}_N(n)e^{-jwn}$，对上式取模平方，除以$N$，即可得到一个“非精确”的谱$\hat{S}(w)=\frac{1}{N}|U_N(w){|}^2$，这就是周期图法的原理。周期图法得到的功率谱

随数据点数$N$的增加，分辨率和方差也变大，这和我们所期望的“分辨率大、方差小”是矛盾的，为了进一步降低方差，将$N$个观测样本数据点$u_N(n)$分为$L$段，每段数据长度为$M$，分别对每段数据求周期图功率谱估计，然后求平均值，这种方法称为平均周期图法。由概率论知识和随机的特性可知，$L$个相同均值和方差$\sigma$的独立变量，$X=\frac{1}{L}{\sum }_1^L{X}_i$，方差变为$\sigma =\frac{1}{L}$，但数据点减小为$\frac{N}{L}$，窗函数的频谱宽度增大为原周期图法的$L$倍，频率分辨率下降为原来的$\frac{1}{L}$，即：

​ $var(\bar{X})=E[{\bar{X}}^2]-E[\bar{X}{]}^2=\frac{1}{L}var(X_i)$

​ 因此，$N$增大时，会带来谱线起伏加剧的问题，功率谱分辨率较低，正比于$\frac{2\pi }{N}$​。窗函数也使得功率谱主瓣展宽，降低了分辨率。因此分段平均改进后的方法降低了估计方差，使得曲线更为平滑。通过图4和图5以及表1可以发现，当分段数$L$增加时，方差虽然变小，但是分辨率也随之变小，细节可见度降低，即当观测样本序列个数$N$固定时，要降低方差需要增加分段数$L$，若分段数$L$固定时，增加分辨率则需要采集到更长的检测数据序列，实际中恰恰是检测样本序列长度不足，因此和周期图法一样，平均周期图法无法兼顾分辨率和方差（当$L=1$时，平均周期图法退化为周期图法）。

然而实际中检测样本序列长度是有限的。对现有数据长度$N$，若能获得更多的段数分割，将得到更小的方差，若允许数据段间有重叠部分，来得到更多的段数，可以在保持一定分辨率的前提下进一步降低方差，这就是$welch$法。因此相比图2和图3，图5得到的功率谱计算结果更平滑，相比直接法和加窗平滑法，方差也更小。