题目大意:求n!在k进制下的位数
即
Stirling公式:
数据范围小就暴力,数据范围大套用Stirling公式
注意先利用log来避免数字过大而失精 最后答案要开long long
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const double pi=acos(-1.0),e=exp(1.0);
int n,k;
int main()
{
int i;
while(~scanf("%d%d",&n,&k) )
{
if(n<=100)
{
double temp=0;
for(i=2;i<=n;i++)
temp+=log(i);
temp/=log(k);
cout<<(long long)floor(temp+1e-7)+1ll<<endl;
}
else
{
double temp=log(2*pi*n)/log(k)/2+n*log(n/e)/log(k);
cout<<(long long)floor(temp+1e-7)+1ll<<endl;
}
}
return 0;
}










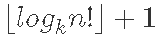
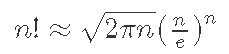














 670
670

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








