cs224w（图机器学习）2021冬季课程学习笔记3: Node Embeddings

诸神缄默不语-个人CSDN博文目录
cs224w（图机器学习）2021冬季课程学习笔记集合

YouTube视频观看地址1 视频观看地址2 视频观看地址3

1. 章节前言

1. 图表示学习graph representation learning：学习到图数据用于机器学习的、与下游任务无关的特征，我们希望这个向量能够抓住数据的结构信息。
   这个数据被称作特征表示feature representation或嵌入embedding。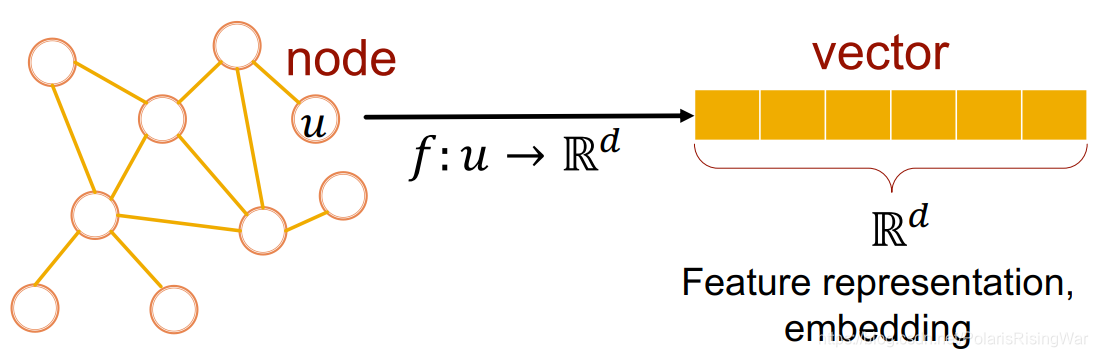
2. Why embedding?
   任务：将节点映射到embedding space
   1. embedding的相似性可以反映原节点在网络中的相似性，比如定义有边连接的点对为相似的点，则这样的点的embedding应该离得更近
   2. embedding编码网络信息
   3. embedding可用于下游预测任务
3. node embedding举例：Zachary’s Karate Club network¹ 的二维节点嵌入可视化（将不同类的节点很好地分开了）
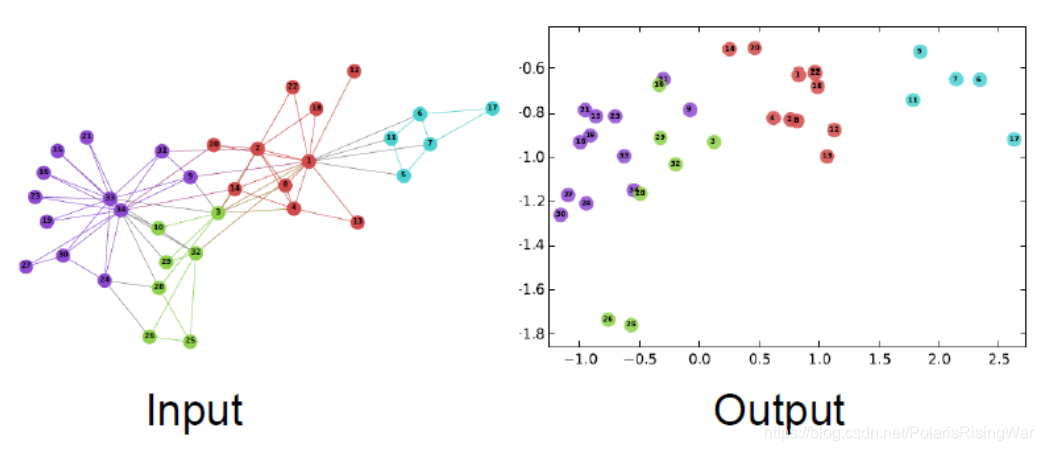   图源：Perozzi et al. DeepWalk: Online Learning of Social Representations. KDD 2014

2. Node Embeddings: Encoder and Decoder

1. 图 $G$，节点集合 $V$，邻接矩阵 $A$（二元的）（简化起见：不考虑节点的特征或其他信息）
2. 节点嵌入：目标是将节点编码encode为embedding space中的向量embedding，使embedding的相似度（如点积²）近似于图中节点的相似度（需要被定义）
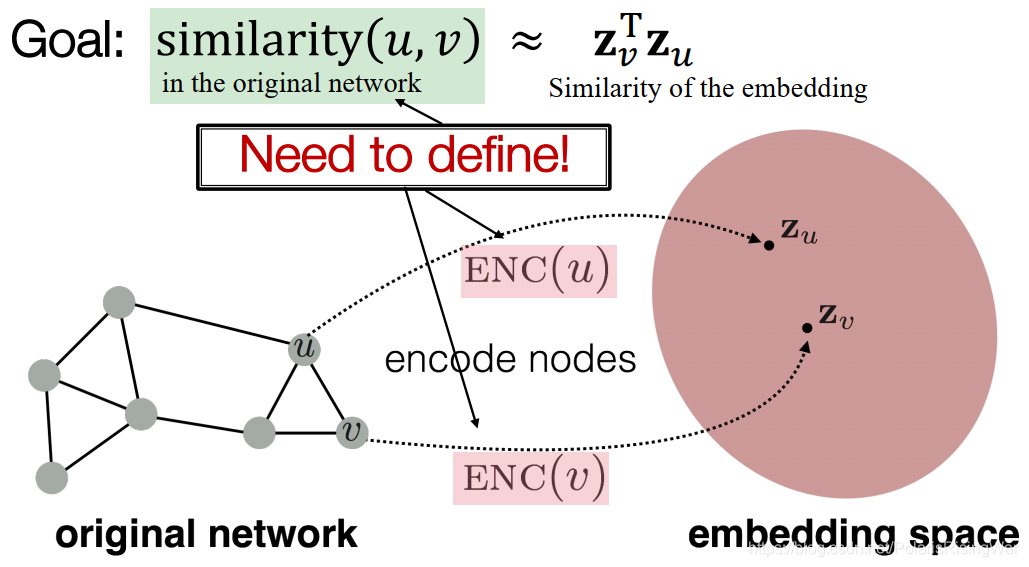
3. Encoder：将节点映射为embedding
   定义一个衡量节点相似度的函数（如衡量在原网络中的节点相似度）
   Decoder DEC 将embedding对映射为相似度得分
   
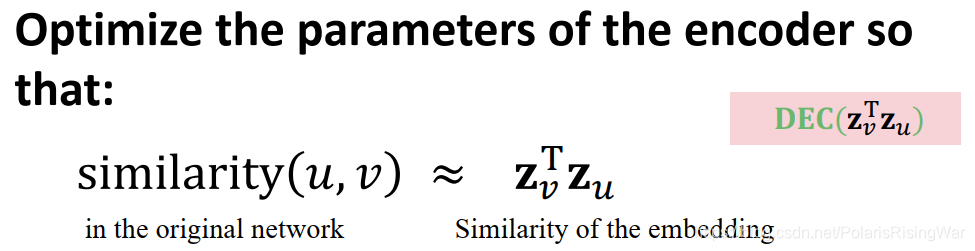
4. two key componentsd一般是64-1000维
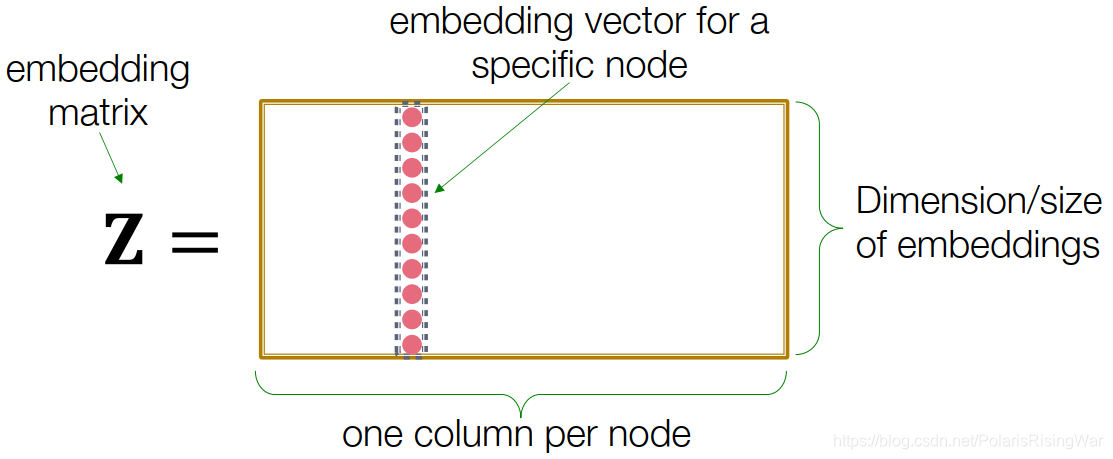5. “shallow” encodingZ每列是一个节点所对应的embedding向量。v是一个其他元素都为0，对应节点位置的元素为1的向量。通过矩阵乘法的方式得到结果。
   这种方式就是将每个节点直接映射为一个embedding向量，我们的学习任务就是直接优化这些embedding。
   缺点：参数多，很难scale up³到大型图上。
   优点：如果获得了Z，各节点就能很快得到embedding。
   有很多种方法：如DeepWalk，node2vec等
6. Encoder + Decoder Framework Summary
   1. Shallow encoder: embedding lookup
   2. 优化参数：Z（包含每个节点对应的node embedding）
   3. 在Lecture 6将介绍deep encoders（已完成对应章节的笔记，见cs224w（图机器学习）2021冬季课程学习笔记7 Graph Neural Networks 1: GNN Model）
   4. Decoder: based on node similarity
   5. 目标：对于相似点对 (u,v)，最大化其embedding点积
7. 节点相似的不同定义
   1. 有边
   2. 共享邻居
   3. 有相似的structural roles
   4. 本节课：随机游走random walk定义的节点相似度
8. Note on Node Embeddings
   1. 无监督/自监督unsupervised/self-supervised：不用节点的标签和特征，直接估算得到节点的一系列坐标（如embedding），这一系列坐标在某种程度上可以保留网络结构（由DEC捕获）
   2. task independent

3. Random Walk Approaches for Node Embeddings

1. 统一符号表示notation
   $P(v|{\mathbf{z}}_u)$ 是从 $u$ 开始随机游走能得到 $v$ 的概率，衡量 $u$ 和 $v$ 的相似性，用节点embedding向量相似性算概率。
   用于计算预测概率的非线性函数：softmax会将一组数据归一化为和为1的形式，最大值的结果会几乎为1。sigmoid会将实数归一化到 (0,1) 上。⁴
2. random walk：从某一节点开始，每一步按照概率选一个邻居，走过去，重复。停止时得到一系列节点
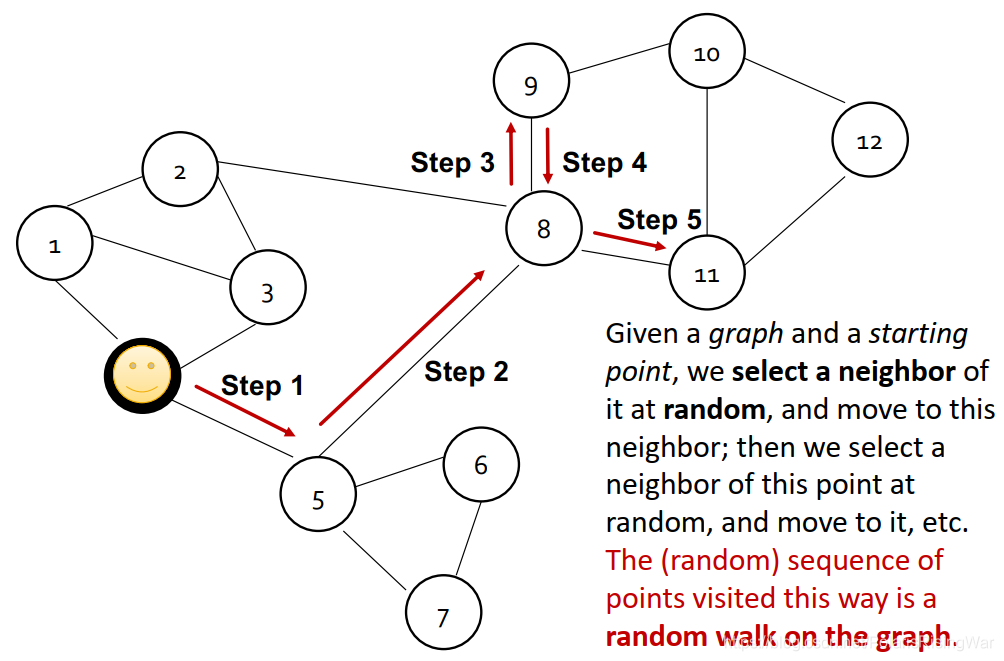
3. random walk embeddings
   ${\mathbf{z}}_u^T{\mathbf{z}}_v\approx$点 $u$ 和 $v$ 在一次随机游走中同时出现（点 $v$ 在以 $u$ 为起点的随机游走中出现）的概率
   
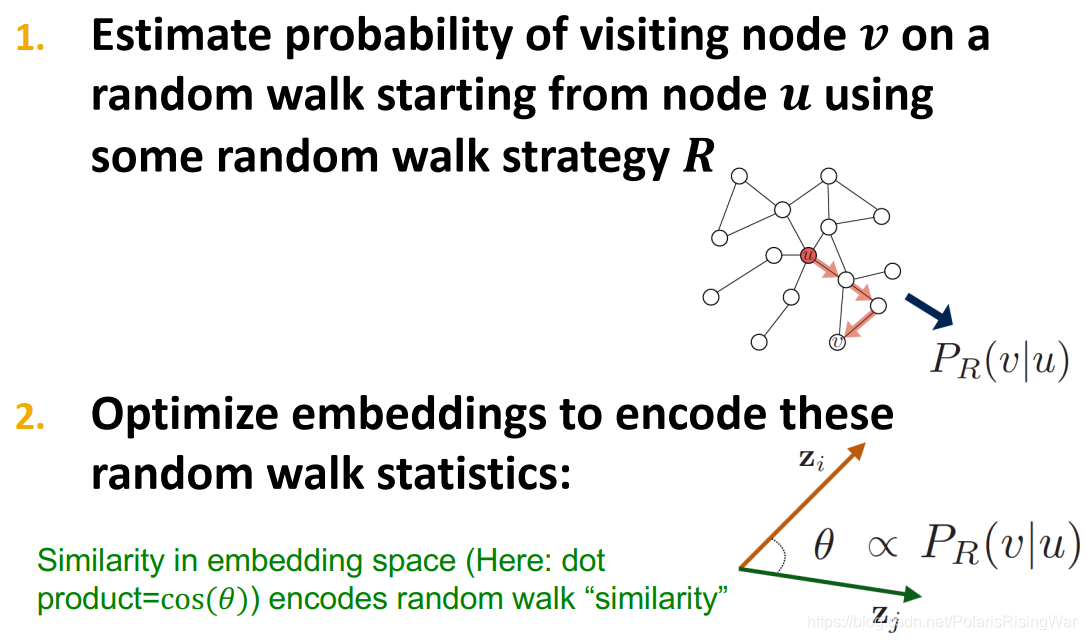
4. Why random walks?
   1. Expressivity: Flexible stochastic definition of node similarity that incorporates both local and higher-order neighborhood information
      Idea: if random walk starting from node 𝒖 visits 𝒗 with high probability, 𝒖 and 𝒗 are similar (high-order multi-hop information)
   2. Efficiency: Do not need to consider all node pairs when training; only need to consider pairs that co-occur on random walks
5. unsupervised feature learning
   1. Intuition: Find embedding of nodes in 𝑑-dimensional space that preserves similarity
   2. Idea: Learn node embedding such that nearby nodes are close together in the network
   3. Given a node 𝑢, how do we define nearby nodes?
      $N_R(u)$ … neighbourhood of 𝑢 obtained by some random walk strategy 𝑅
6. feature learning as optimization
   目标是使对每个节点 $u$，$N_R(u)$ 的节点和 ${\mathbf{z}}_u$ 靠近，即 $P(N_R(u)|{\mathbf{z}}_u)$ 值大。
   $f$: $u\to {\mathbb{R}}^d$: $f(u)={\mathbf{z}}_u$
   log-likelihood⁵目标函数：$\underset{f}{\max }\sum _{u\in V}\log P(N_R(u)|{\mathbf{z}}_u)$
   对这个目标函数的理解是：对节点 $u$，我们希望其表示向量对其random walk neighborhood $N_R(u)$ 的节点是predictive的（可以预测到它们的出现）
7. random walk optimization
   
   把最大似然估计翻过来，拆开，就成了需被最小化的损失函数L：这个计算概率 $P(v|{\mathbf{z}}_u)$ 选用softmax的intuition就是前文所提及的，softmax会使最大元素输出靠近1，也就是在节点相似性最大时趋近于1。
   将 $P(v|{\mathbf{z}}_u)$ 代入L得：
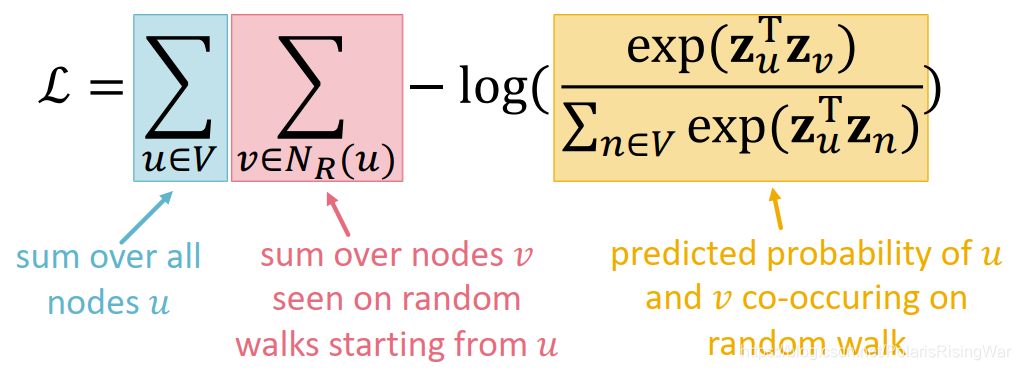
   优化random walk embeddings就是找到embedding $\mathbf{z}$ 使L最小化
   
   但是计算这个公式代价很大，因为需要内外加总2次所有节点，复杂度达$O(|V{|}^2)$：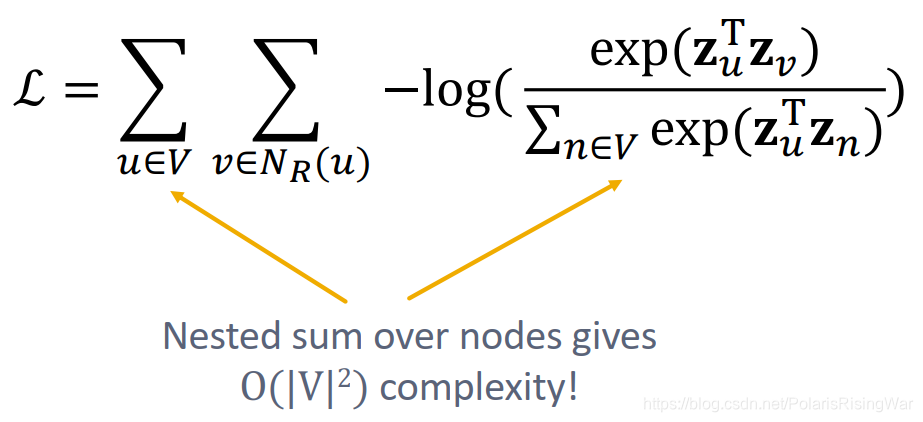
   我们发现问题就在于用于softmax归一化的这个分母：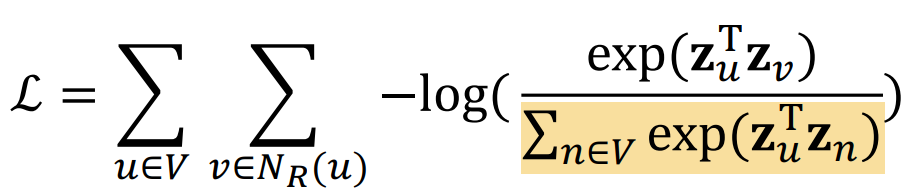
8. 为了解决这个分母，我们使用negative sampling⁶的方法：简单来说就是原本我们是用所有节点作为归一化的负样本，现在我们只抽出一部分节点作为负样本，通过公式近似减少计算
   
   这个随机分布不是uniform random，而是random in a biased way：概率与其度数成比例。
   
   负样本个数k的考虑因素：
   1. 更高的k会使估计结果更鲁棒robust（我的理解是方差↓）
   2. 更高的k会使负样本上的偏差bias更高（其实我没搞懂这是为什么）
   3. 实践上的k常用值：5-20
9. 优化目标函数（最小化损失函数）的方法：随机梯度下降SGD
10. random walks: summary
11. random walk策略
    1. Simplest idea: Just run fixed-length, unbiased random walks starting from each node
       举例：DeepWalk⁷
       问题：相似度概念受限
    2. node2vec⁸
       1. 原因：有弹性的网络邻居 $N_R(u)$ 定义使 $u$ 的embedding更丰富，因此使用有偏的二阶⁹随机游走策略 biased $2^{nd}$ order random walk 以产生 $N_R(u)$
       2. biased walks
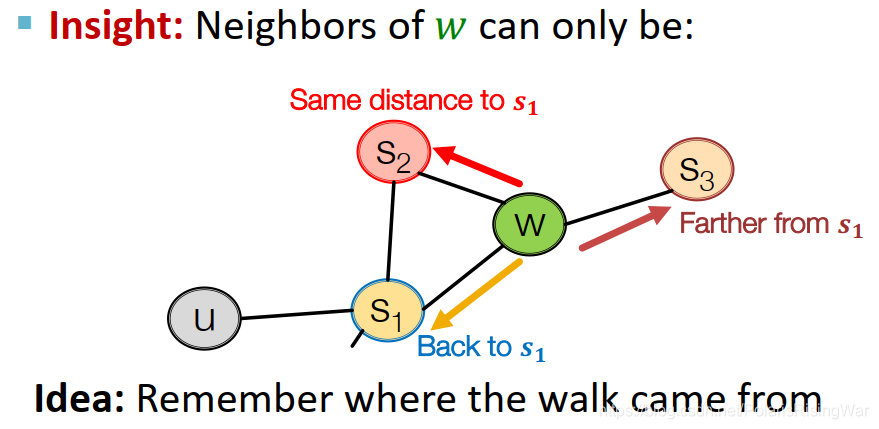
          用有弹性、有偏的随机游走策略平衡local（BFS）和global（DFS）的节点网络结构信息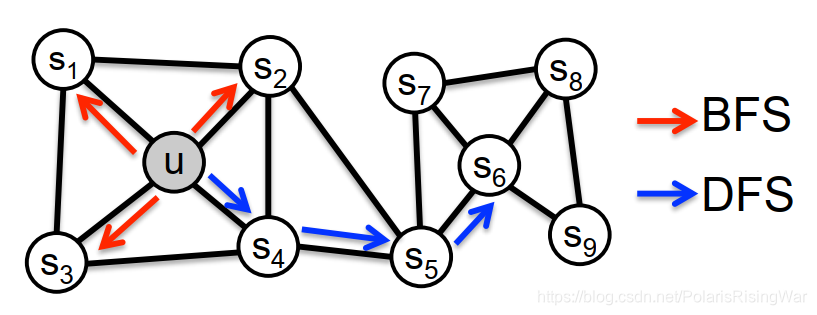
          
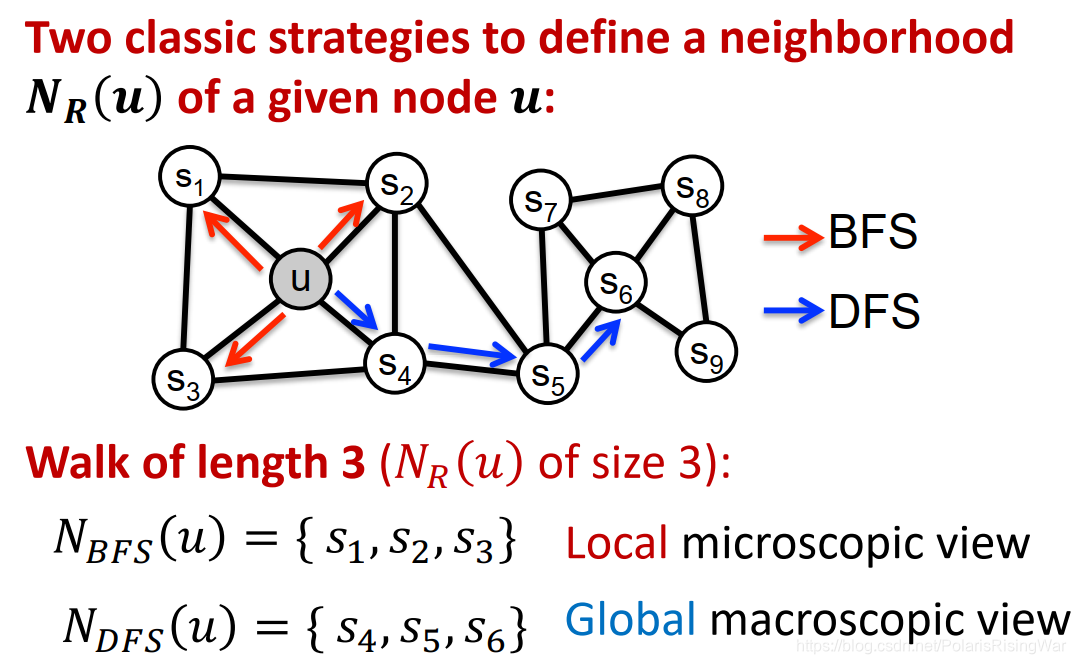
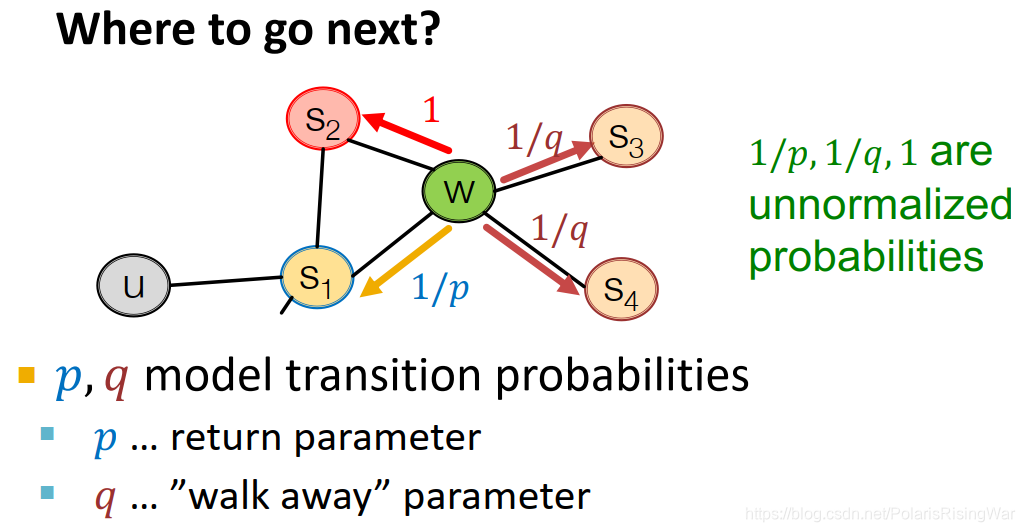
       3. 有偏定长随机游走的参数：
          1. return parameter $p$：返回上一个节点的概率
          2. in-out parameter $q$：向外走（DFS）VS向内走（BFS）
             相比于DFS，选择BFS的概率
       4. 有偏随机游走举例
          上一步是 ($s_1$,$w$)
          
          BFS-like walk会给p较低的值，DFS-like walk会给q较低的值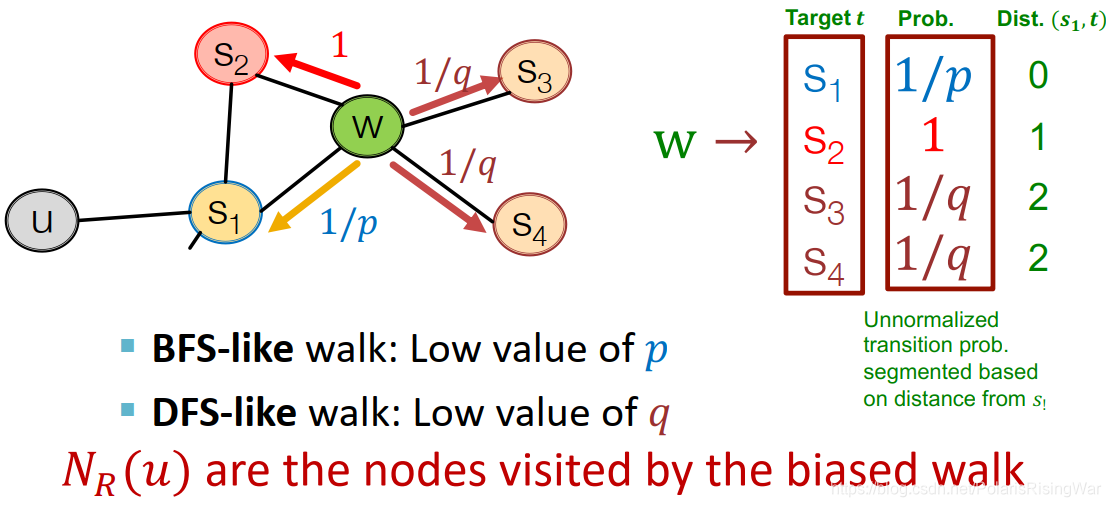
       5. node2vec算法¹⁰线性时间复杂度是因为节点邻居数量是固定的
    3. 其他随机游走方法¹¹：
12. Summary so far
    1. 节点嵌入：使embedding的向量距离能够反应原网络中的节点相似度
    2. 衡量节点相似度的指标
       1. Naive: 节点间有边
       2. Neighborhood overlap （在Lecture 2¹² 讲过）
       3. random walk approaches（本节课所讲）
    3. 需要根据具体情况来选择算法。node2vec在节点分类任务上表现更好，不同的方法在不同数据的链接预测任务上表现不同¹³。random walk approaches整体上更有效。

4. Embedding Entire Graphs

任务目标：嵌入子图或整个图 $G$，得到表示向量 ${\mathbf{z}}_G$

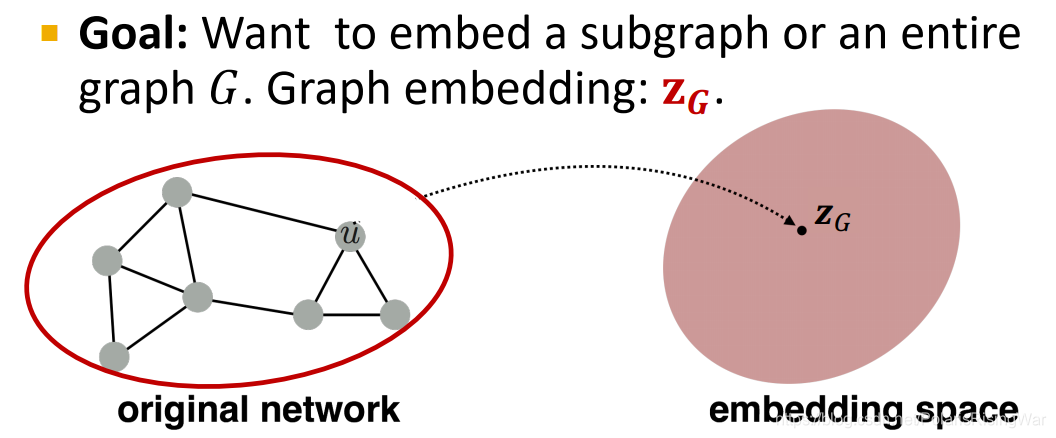
任务示例：

• 分类有毒/无毒分子
• 识别异常图

也可以视为对节点的一个子集的嵌入

1. 方法1：聚合（加总或求平均）节点的嵌入
   ${\mathbf{z}}_G=\sum _{v\in G}{\mathbf{z}}_v$
   示例：Duvenaud D, Maclaurin D, Aguilera-Iparraguirre J, et al. Convolutional networks on graphs for learning molecular fingerprints[J]. arXiv preprint arXiv:1509.09292, 2015. 用图结构对分子进行分类。虽然方法很简单但是表现挺好。
2. 方法2：创造一个假节点（virtual node），用这个节点嵌入来作为图嵌入
   这个virtual node和它想嵌入的节点子集（比如全图）相连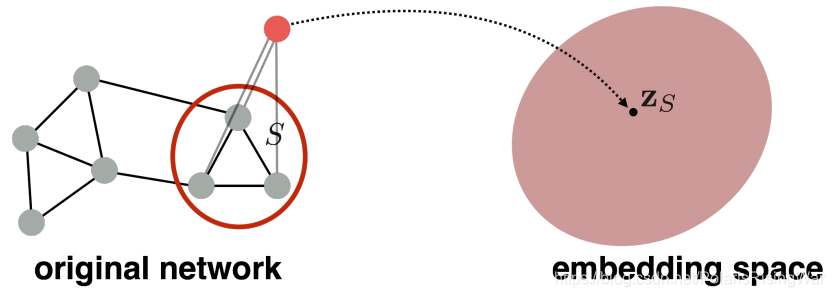
   示例：Li Y, Tarlow D, Brockschmidt M, et al. Gated graph sequence neural networks[J]. arXiv preprint arXiv:1511.05493, 2015.
3. 方法3：anonymous walk embeddings¹⁴（以节点第一次出现的序号（是第几个出现的节点）作为索引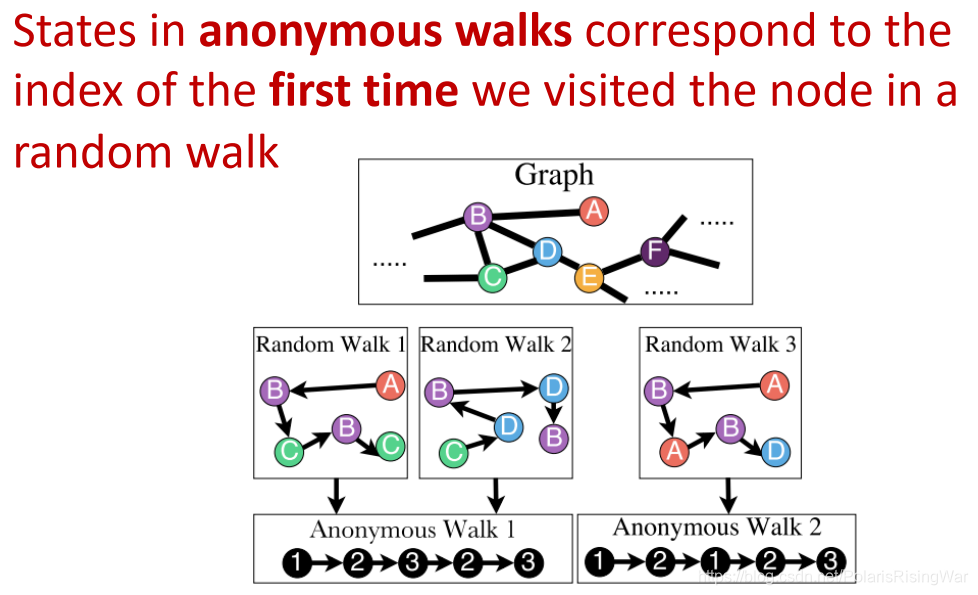）这种做法会使具体哪些节点被游走到这件事不可知（因此匿名）
   1. anonymous walks的个数随walk长度指数级增长：
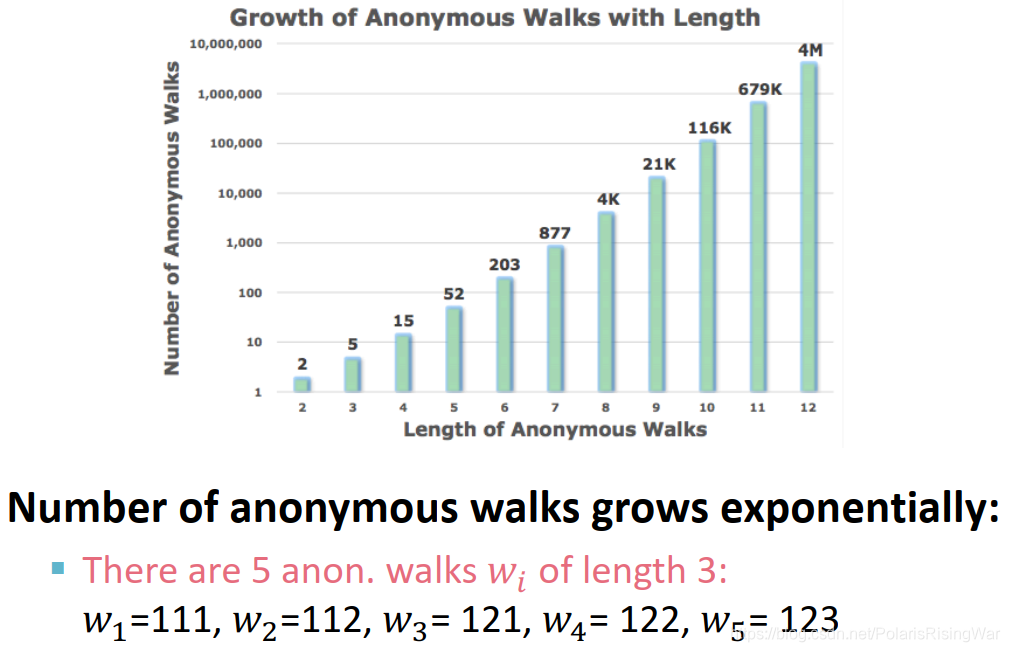
   2. anonymous walks的应用1：模拟图上长为 $l$ 的匿名随机游走，将图表示为walks的概率分布向量（我感觉有点bag-of-anonymous walks、有点像GDV那些东西，总之都是向量每个元素代表其对应object的出现概率/次数）
   3. sampling anonymous walks（图中这个m我还不知道是从哪来的）
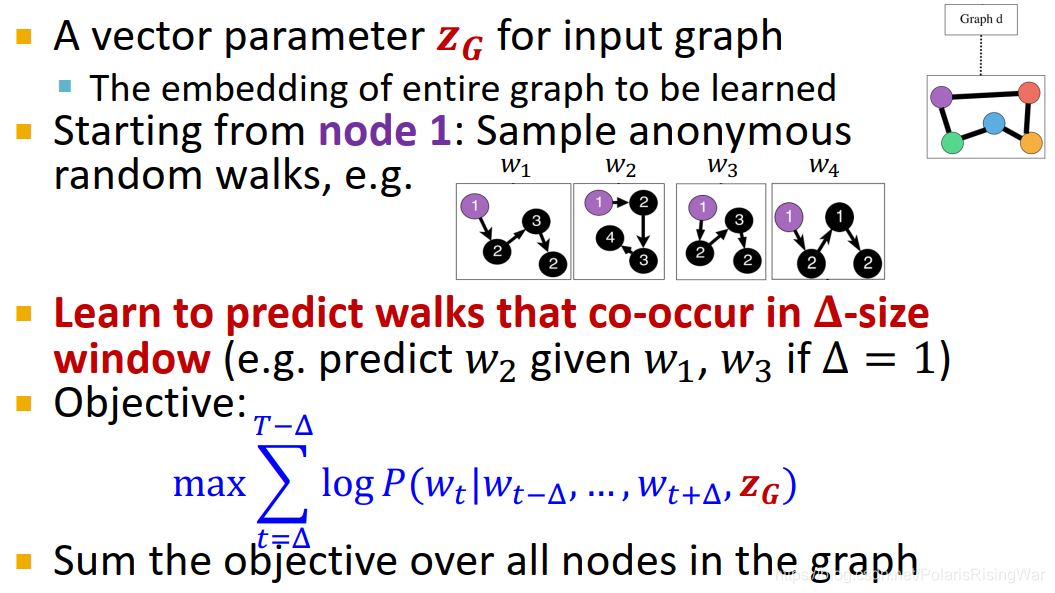
   4. anonymous walks的应用2：walk embeddings
      学图嵌入 ${\mathbf{Z}}_G$ 和匿名游走嵌入 ${\mathbf{z}}_i$ Z = { z i : i = 1... η } Z=\{\mathbf{z}_i:i=1...\eta\} Z={zi​:i=1...η}
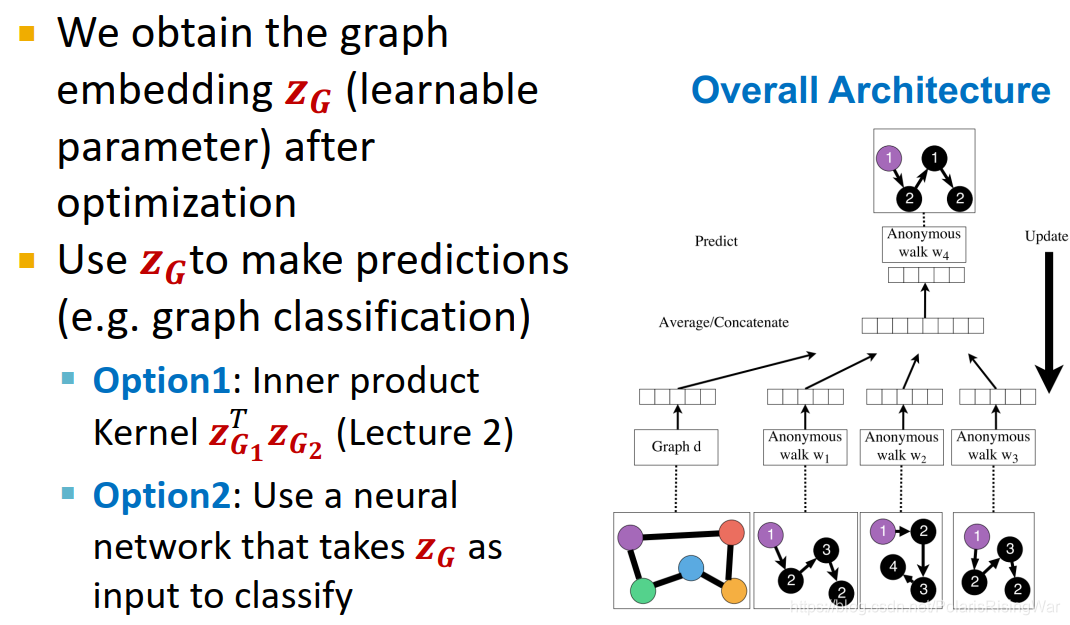
      具体算法没太看懂，我觉得是要求特定游走窗口下出现特定游走的概率（用窗口内游走嵌入的聚合进行了一个线性转换，然后用softmax转换得到（图上的公式好像写错了，但是我不太确定，因为我也没太搞懂））最高。而且我也没搞懂 ${\mathbf{Z}}_G$ 是怎么连上来的，这个cat就硬连吗？有缘看论文吧，图机器学习太难了，我总在接受自己的无知和命运的不可预测。
      得到 ${\mathbf{Z}}_G$ 后可用于预测任务，可以视其内积为核，照第二章¹²所介绍的核方法来进行机器学习；也可以照后续课程将介绍的神经网络方法来进行机器学习。
      
4. Summary
5. Lecture 8中会讲到Hierarchical Embeddings方法，分层级聚合图中节点获得全图嵌入向量

5. 本章总结

1. 如何使用节点嵌入：聚类、社区发现，节点分类，链接预测（通过concatenate、哈达玛积、取平均、求和、计算距离来得到链接嵌入），图分类（聚合节点嵌入或使用匿名随机游走获得图嵌入）哈达玛积、sum/avg、L2距离在无向图上表现好，因为它们是commulative的（就是交换参数对结果没有影响）；如果是有向图的话concatenate就会好
2. Summary

6. 文中及脚注未提及的其他参考资料

1. 图神经网络（03）-Node Embeddings 和鲸平台上一位用户撰写的笔记

---

1. 该数据集的详细介绍见：图数据集Zachary‘s karate club network详解，包括其在NetworkX、PyG上的获取和应用方式 ↩︎

2. 衡量向量的相似有很多种方式，在本课程中主要用到两种：一是点积相似度，二是余弦相似度。
   在本课程中开篇称使用的是点积相似度，但后文称点积相似度就是余弦相似度，我有点没搞懂这个是啥意思，节点嵌入向量模长不一定会相等吧？这两个相似度会一样吗……
   但是在colab 1中用的是点积相似度。而且感觉上点积相似度应该会更好计算一些。
   参考资料：点积相似度、余弦相似度、欧几里得相似度 ↩︎

3. 本课程后期将会专门讲图机器学习方法如何scale up到大型图上，我也计划继续撰写相应笔记。 ↩︎

4. softmax是一个soft的max（见参考资料①）。
   具体的我也没太了解，反正就是如正文所说这么一回事吧，具体细节以后再学。（为什么明明根本看不懂的资料还好意思管自己叫简单啊？）
   参考资料：
   ①Sigmoid 函数和 Softmax 函数的区别和关系
   ②二分类问题，应该选择sigmoid还是softmax？（读芯术有一篇推文作为答案发在了问题里，百家号原推文：函数分类大PK：Sigmoid和Softmax，分别怎么用？
   ③Softmax 原理及 Sigmoid和Softmax用于分类的区别
   ④小白都能看懂的softmax详解
   ⑤多类分类下为什么用softmax而不是用其他归一化方法?
   ⑥浅谈sigmoid函数和softmax函数 ↩︎

5. 总之极大似然估计大概差不多就是我们认为现实发生的情况就是最有可能发生的情况，所以在未知参数的情况下写出发生现实情况的概率公式，认为使其最大的参数就是我们所需的参数。所以最大化这个公式，就能得到我们要的参数。
   因为对连乘取log会使其更便于计算，所以一般会对其取log。
   比如这个公式就是将每个节点的概率进行连乘，每个节点的概率即得到我们希望最有可能发生的情况——概率最大化，即在空间域上相近（random walk邻居和原节点）的节点向量域上最近。能够满足这个条件的f就是我们所需的参数。
   ……
   ……
   ……
   其实我没搞懂，我也觉得我理解的东西没讲清楚，但是不管了，总之大概或许就是这么一回事吧，统计学的东西我以后再研究好了。
   参考资料：
   ①对数似然函数值/最大近然估计/log likelihood
   ②似然与极大似然估计
   ③最大似然估计的理解(Maximum likelihood estimation） ↩︎

6. colab 1中有类似的抽取负样本的操作，可见我写的colab 1笔记：cs224w（图机器学习）2021冬季课程学习笔记5 Colab 1：Node Embeddings_诸神缄默不语的博客-CSDN博客
   这个公式如何近似成这样的，我还没搞懂，softmax变sigmoid是啥操作我也没搞懂，以后要是有缘分会去看课程中给出的参考资料：word2vec Explained: Deriving Mikolov et al.’s Negative-Sampling Word-Embedding Method ↩︎

7. 课程中提供的论文下载地址：DeepWalk: Online Learning of Social Representations ↩︎

8. 课程中提供的论文下载地址：node2vec: Scalable Feature Learning for Networks ↩︎

9. DeepWalk是比较简单的一阶随机游走。
   对这个概念的解释可以参考 Remember Where You Came From: On The Second-Order Random Walk Based Proximity Measures 一文（我只看了摘要），大致来说就是，一阶随机游走每一步都仅考虑节点当前位置，二阶随机游走还考虑节点上一步的位置。 ↩︎

10. 我没搞懂这三步为什么可以并行计算……有缘分了我再去看论文吧，这对现在的我来说太为难了 ↩︎

11. 图中链接依次：
    metapath2vec: Scalable Representation Learning for Heterogeneous Networks
    Watch Your Step: Learning Node Embeddings via Graph Attention
    LINE: Large-scale Information Network Embedding
    struc2vec: Learning Node Representations from Structural Identity 这一篇课程中应该写错了，而且链接也给错了
    HARP: Hierarchical Representation Learning for Networks ↩︎

12. 可以参考我之前写的笔记：cs224w（图机器学习）2021冬季课程学习笔记2 ↩︎ ↩︎

13. 课程中提供的论文下载地址：Graph Embedding Techniques, Applications, and Performance: A Survey ↩︎

14. 课程中提供的论文下载地址：Anonymous Walk Embeddings ↩︎