KL社区发现算法概述与源码

本文在实现KL算法的过程中实现了社区划分结果，同时实现了不同社区的可视化结果。

---

GN社区发现算法传送门

---

author：xiao黄
缓慢而坚定的生长
公众号：Community Detection
本人更新在csdn关于社区发现（Community Detection）方面的知识会同步更新到公众号中。

---

KL算法介绍

Kernighan-Lin算法是一种试探优化的方法，其基本的思想是为网络引入一个试探函数Q，Q代表某两个准社团内部的边数减去两个准社团之间的边数的差值，然后得到使Q值最大的划分方法。

首先将整个网络的节点随机的或根据网络的现有信息分为两个部分，在两个社团之间考虑所有可能的节点对，试探交换每对节点并计算交换后的ΔQ，ΔQ=Q交换后-Q交换前，记录ΔQ最大的交换节点对，并将这两个节点互换，记录此时的Q值。规定每个节点只能交换一次，重复这个过程直至网络中的所有节点都被交换一次为止。需要注意的是不能在Q值发生下降时就停止，因为Q值不是单调增加的，既使某一步交换会使Q值有所下降，但其后的一步交换可能会出现一个更大的Q值。在所有的节点都交换过之后，对应Q值最大的社团结构即被认为是该网络的理想社团结构。

KL算法是将网络分成两个指定规模大小的社区。

算法参数介绍

kernighan_lin_bisection(G, partition=None, max_iter=10, weight=‘weight’, seed=None)
G：图
partition：（元组格式）一对包含初始分区的iterables。如果未指定，则使用随机平衡分区。
max_iter：尝试交换在放弃前找到改进的最大次数。
weight：权重。如果没有，则所有权重都设置为1。
seed：随机数生成状态的指示器。
return：表示两个社区的一对节点。
返回类型：tuple(元组)

代码

import networkx as nx
import matplotlib.pyplot as plt
from networkx.algorithms import community  
from networkx.algorithms.community import kernighan_lin_bisection



def draw_spring(G,com):
    '''
    G:图
    com：划分好的社区
    node_size表示节点大小
    node_color表示节点颜色
    node_shape表示节点形状
    with_labels=True表示节点是否带标签
    '''
    pos = nx.spring_layout(G) # 节点的布局为spring型
    NodeId = list(G.nodes())
    node_size = [G.degree(i)**1.2*90 for i in NodeId] # 节点大小

    plt.figure(figsize = (8,6)) # 图片大小
    nx.draw(G,pos, with_labels=True, node_size =node_size, node_color='w', node_shape = '.')
    
    color_list = ['pink','orange','r','g','b','y','m','gray','black','c','brown']
    # node_shape = ['s','o','H','D']

    for i in range(len(com)):
        nx.draw_networkx_nodes(G, pos, nodelist=com[i], node_color=color_list[i],  with_labels=True)
    plt.show()

if __name__ == "__main__":
    G = nx.karate_club_graph() # 空手道俱乐部

    # KL算法
    com = list(kernighan_lin_bisection(G))
    print('社区数量', len(com))
    print(com)
    draw_spring(G,com)

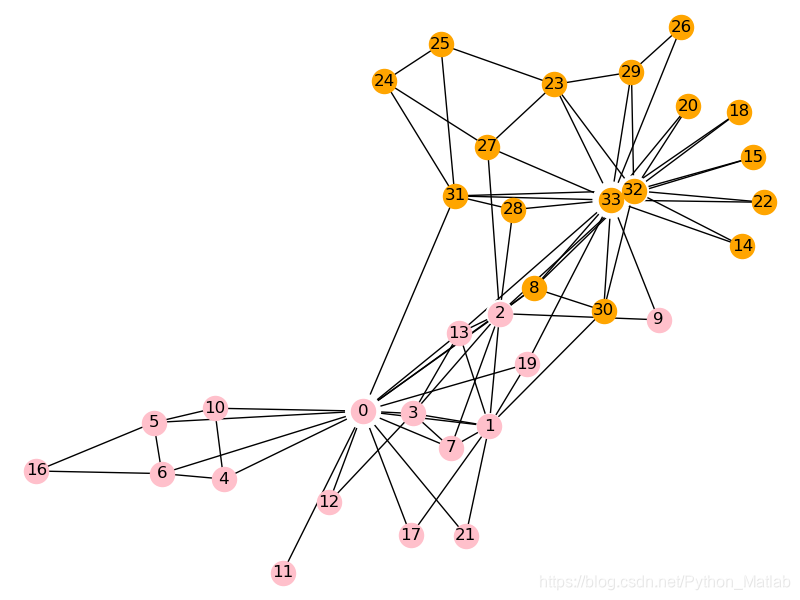
结果：
这就是KL算法划分的结果，分为两个社区，用不同的颜色表示出来。
可以用print(com)语句查看划分后社区中的节点。

参考文献：Kernighan B W, Lin S. A efficient heuristic procedure for partitioning graphs. Bell System Technical Journal, 1970 (49): 291-307.
论文地址：传送门