如何判断一个字符串是不是回文字符串以及字符串的排列组合问题

所谓回文字符串，就是一个字符串，从左到右读和从右到左读是完全一样的，比如"aba"。

题目：判断一个字符串是否为回文

解法：递归

递归的作用在于把问题的规模不断缩少，直到问题缩少到能简单地解决

问：如何缩少问题规模？

答：通过观察可以知道，一个回文字符串其中内部也是回文。所以，我们只需要以去掉两端的字符的形式一层层检查，每一次的检查都去掉了两个字符，这样就达到了缩少问题规模的目的。

新问题与原问题有着相同的形式

当去掉两端字符后的字符串，其产生的新问题同样是检查这个字符串是否回文。

递归的结束需要简单情景

1. 字符串长度可能会奇数或偶数：

• 如果字符串长度是奇数，字符串会剩下最中间那位字符，但其不影响回文。当检查到长度为1的时候即代表此字符串是回文
• 如果字符串长度是偶数，当两端的字符串两两比较检查后不会剩下字符。即检查到长度为0的时候即代表此字符串是回文

2. 如果检查到两端两个字符不相同。则说明此字符串不是回文，直接返回0，不需要继续检查

#include <iostream>
#include <cstring>
#include <cstdio>
#include <string>

using namespace std;

int fun(int l, int r, string str, int len)
{
	if (0 == len || 1 == len)
		return 1;
	if (str[l] != str[r])
		return 0;
	return fun(l + 1, r - 1, str, len - 2);
}

int main()
{
	string ss;
	while (getline(cin, ss))
	{
		cout << fun(0, ss.size() - 1, ss, ss.size()) << endl;;
	}
	system("pause");
}

问题1 ：输入一个字符串，打印出该字符串中字符的所有排列。例如输入字符串abc，则输出由字符a、b、c所能排列出来的所有字符串abc、acb、bac、bca、cab和cba。

    思路：这是个递归求解的问题。递归算法有四个特性：（1)必须有可达到的终止条件，否则程序将陷入死循环；（2）子问题在规模上比原问题小；（3）子问题可通过再次递归调用求解；（4）子问题的解应能组合成整个问题的解。

    对于字符串的排列问题。如果能生成n - 1个元素的全排列，就能生成n个元素的全排列。对于只有1个元素的集合，可以直接生成全排列。全排列的递归终止条件很明确，只有1个元素时。下面这个图很清楚的给出了递归的过程。

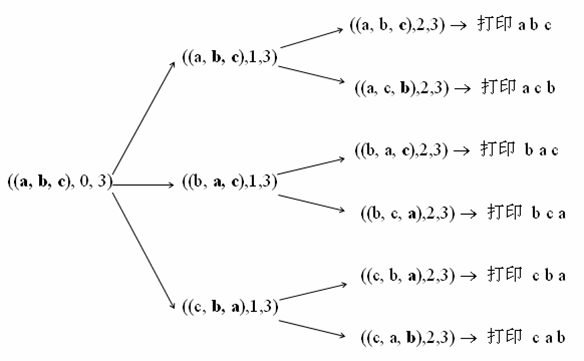
    参考代码：解法1通过Permutation_Solution1(str, 0, n); 解法2通过调用Permutation_Solution2(str, str)来求解问题。

[cpp]  view plain   copy

  print ?

1. //函数功能 ： 求一个字符串某个区间内字符的全排列  
2. //函数参数 ： pStr为字符串，begin和end表示区间  
3. //返回值 ：   无  
4. void Permutation_Solution1(char *pStr, int begin, int end)  
5. {  
6.     if(begin == end - 1) //只剩一个元素  
7.     {  
8.         for(int i = 0; i < end; i++) //打印  
9.             cout<<pStr[i];  
10.         cout<<endl;