【论文阅读】Deep Learning for Image Super-resolution: A Survey（DL超分辨率最新综述）

博主最近看了一篇2019年最新的非常详细的超分辨率领域DL方法的综述，大大地赞！写得非常好，文章工作整理地非常完善！所以想整理成文章发表，留作以后看，哈哈哈哈哈~~

Abstract

摘要部分：作者先讲述了超分辨率(SR)问题的定义和状况，图像超分辨率（SR）是图像处理的一个典型问题，用于增强图像或者视频的分辨率，属于CV领域。目前深度学习在CV领域有很高的建树，该文章就从头梳理DL的超分辨率算法，研究者将图像超分辨分成三种类型：监督SR，无监督SR，特定应用领域的SR。下面就问题定义，方法简述，模型组件，分类，数据集等方面展开介绍。

Introduction

问题定义： 图像超分辨率指的是从低分辨率图像（LR）恢复成高分辨率图像（HR ）的过程。这个技术的应用领域非常广泛，如医学图像，遥感图像，加密等。纵览所有的文献，典型的SR方法有包括几种：基于边缘，基于预测，统计模型，基于块还有稀疏表示等等。而基于深度学习的方法也有以下几种区别：不同类型的网络结构，不同类型的损失函数，不同类型的学习策略。
文章贡献：

• ‌给出一个基于深度学习的图像超分辨技术概要性的回顾，包括问题设定，基准数据集，评价指标，SR方法，特定领域的应用等。
• 提供一个系统性的纵览，总结SR方法中每个组件的优点和局限性； ‌讨论了未来机遇和挑战。

文章安排：

—图1：展示图像超分辨率的分类
—第二部分：给出问题的定义和回顾主流的数据集和评价指标
—第三部分：分析有监督的超分辨率主要部件
—第四部分：给出无监督超分辨率方法的简要介绍
—第五部分：介绍主流的SR特定应用领域
—第六部分：讨论未来的方向和开源问题

section 1：

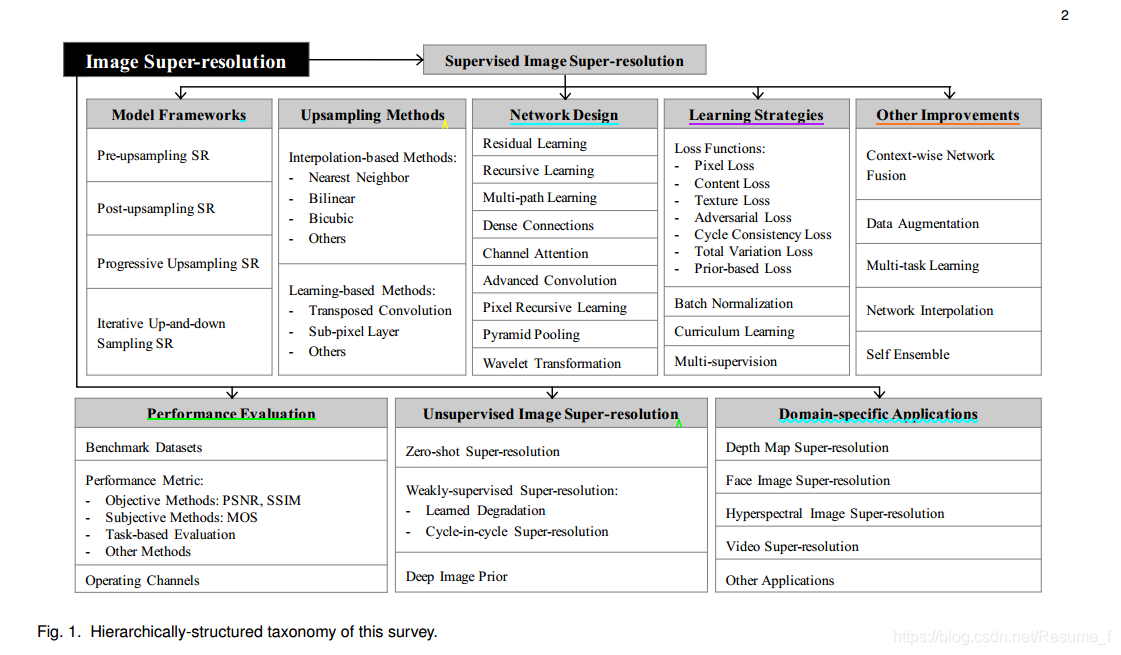
不得不说，这图真的太赞了！清晰明了，这对于我这种刚接触一个新领域的小白来说，一篇好的综述能帮助好多，理清思路。在第一部分，我就根据表格的内容，简单地做个中文版。（有些专业术语不会翻译，就不翻了，免得写错，哈哈哈英语水平有待提高）

1. 监督学习的超分辨率

• 模型框架

   	1.提前上采样
   	2.最后上采样
   	3.渐近式上采样
   	4.迭代交替式上下采样
  

• ‌上采样方法

    1.基于传统的插值方法
    	最近邻
    	双线性
    	双三次方
    	其他
    2.基于学习的方法
    	反卷积
    	亚像素层
    	其他
  

• 网络设计

   	残差学习
   	递归学习
   	多路径学习
   	紧密连接
   	通道注意力机制
   	高级卷积
   	像素递归学习
   	金字塔池化
   	小波变换
  

• 学习策略

   	1.损失函数
   		正则化
   		‌其他
   	2.curriculum learning ( 不好用中文表述）
   	3.多监督学习
  

• 其他

   	上下文融合网络
   	数据增强
   	多任务学习
   	网络插值
   	self Ensemble
  

• ‌评价指标

   	1.数据集
   	2.指标
   		客观方法: PSNR，SSIM
   		主观方法: MOS
   		基于任务评估
  

2. 无监督SR ‌ (该领域不是我所涉及的，在这不详细介绍）

3. 特定领域应用 （粗略介绍）

Problem Definition

问题定义：其实上面也有大概描述了一下。准确来说，超分辨率的过程是将LR恢复成HR，通常，LR图像$I_x$是经过我们本来拥有的高清图$I_y$（叫ground truth）降质得到的，公式如下：
$$I_x=D(I_y;\theta ）$$
这里D是降质的过程，代表着一个下采样函数，参数$\theta$代表采样因子等。而一般情况下只采用一个函数就可用对高清图进行降质了，有些情况也可以使用一个卷积层或模型来完成降质过程。
而超分辨率这个过程是，将降质后的低分辨率图像$I_x$还原成高分辨图像$I_y^{\prime }$，这里用公式表述：
$$I_y^{\prime }=F(I_x;\alpha )$$

F代表着超分辨率模型，$\alpha$代表F的参数。这里重建后的图像和原来的高清图会有一些差别，因此在深度学习上，就用损失函数来衡量，以优化两者的差别达到重建效果相近。
$${\theta }^{\prime }=argmi{n}_{\theta }L(I_y,I_y^{\prime })+\lambda \Phi (\theta )$$
后面的$\lambda \Phi (\theta )$代表的是正则化项。

Datasets for SR

这里列举了超分辨率领域的一些常用公开的数据集，下面把链接贴上来。
(表格来源是Github上一位大佬的, 他的github地址贴上来：https://github.com/LoSealL/VideoSuperResolution）

Model	Published	Code*	VSR (TF)**	VSR (Torch)	Keywords	Pretrained
SRCNN	ECCV14	-, Keras	Y	Y	Kaiming	√
RAISR	arXiv	-	-	-	Google, Pixel 3
ESPCN	CVPR16	-, Keras	Y	Y	Real time	√
VDSR	CVPR16	-	Y	Y	Deep, Residual	√
DRCN	CVPR16	-	Y	Y	Recurrent
DRRN	CVPR17	Caffe, PyTorch	Y	Y	Recurrent
LapSRN	CVPR17	Matlab	Y	-	Huber loss
EDSR	CVPR17	-	Y	Y	NTIRE17 Champion	√
SRGAN	CVPR17	-	Y	-	1st proposed GAN
VESPCN	CVPR17	-	Y	Y	VideoSR	√
MemNet	ICCV17	Caffe	Y	-
SRDenseNet	ICCV17	-, PyTorch	Y	-	Dense	√
SPMC	ICCV17	Tensorflow	T	Y	VideoSR
DnCNN	TIP17	Matlab	Y	Y	Denoise	√
DCSCN	arXiv	Tensorflow	Y	-
IDN	CVPR18	Caffe	Y	-	Fast	√
RDN	CVPR18	Torch	Y	-	Deep, BI-BD-DN
SRMD	CVPR18	Matlab	T	-	Denoise/Deblur/SR
DBPN	CVPR18	PyTorch	Y	Y	NTIRE18 Champion	√
ZSSR	CVPR18	Tensorflow	-	-	Zero-shot
FRVSR	CVPR18	PDF	T	Y	VideoSR	√
DUF	CVPR18	Tensorflow	T	-	VideoSR
CARN	ECCV18	PyTorch	Y	Y	Fast	√
RCAN	ECCV18	PyTorch	Y	Y	Deep, BI-BD-DN
MSRN	ECCV18	PyTorch	Y	Y		√
SRFeat	ECCV18	Tensorflow	Y	Y	GAN
NLRN	NIPS18	Tensorflow	T	-	Non-local, Recurrent
SRCliqueNet	NIPS18	-	-	-	Wavelet
FFDNet	TIP18	Matlab	Y	Y	Conditional denoise
CBDNet	arXiv	Matlab	T	-	Blind-denoise
SOFVSR	ACCV18	PyTorch	-	Y	VideoSR	√
ESRGAN	ECCVW18	PyTorch	-	Y	1st place PIRM 2018	√
TecoGAN	arXiv	Tensorflow	-	T	VideoSR GAN	√
RBPN	CVPR19	PyTorch	-	Y	VideoSR	√

*The 1st repo is by paper author.

**Y: included(包括）; -: not included（不包括）; T: under-testing（测试不足）.

Image Quality Assessment

图像评估指标：有主观方法和客观方法，但是这两种方法的侧重点不一致，并不能很好地统一说明图像质量优劣。主观方法是人为的，带有主观性！而常用的客观方法有PSNR，MSE，SSIM。其中PSNR叫峰值信噪比，是计算ground truth（简称GT）和重建的HR之间像素级的差异；SSIM叫结构相似度，是计算GT和HR之间亮度通道的相似度。
PSNR的公式依赖于MSE（均方差）计算，给定GT为$I$，重建的图像为$I^{\prime }$，公式如下：
$$MSE=\frac{1}{N}\sum _{i=1}^N(I(i)-I^{\prime }(i){)}^2$$
$$PSNR=10\ast lg(\frac{L^2}{MSE})$$
一般我们的使用的图像都是8位，L代表着0-255的最大值，即255。
SSIM公式就分开了三种，公式有点多，这里贴出我之前写的一篇文章作参考，https://blog.csdn.net/Resume_f/article/details/103339722，先把公式放上来，具体解释就不展开了。
$$l$$