C语言递归算法系列_汉诺塔(6)

这次我们接触一个抽象程度更高的递归问题，hanoi塔。

问题描述为：汉诺塔是由三根杆子A，B，C组成的。A杆上有N个(N>1)穿孔圆盘，盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至C杆：每次只能移动一个圆盘；大盘不能叠在小盘上面。

这个问题在显示中还真没什么用处，但是基本讲解递归问题就会把它拿出来。

既然是递归，那我们还是按照分析递归问题的步骤来。

我们设定这样的函数原型

void hanoi(int n, char start, char temp, char target);

参数n表示当前移动的几号盘，从小到大1~n。start表示当前盘的位置，target表示要移动的位置，temp表示临时放用于过渡的位置。

1.最简单的情况，那就是只有一个盘在A杆，那么只需要将其移到C杆就行。

2.如果是多个盘，首先得将最大的盘移动到目标杆上去，要达成这一目标，需要把n-1个较小的盘借助target杆移动到temp杆，这样才能不破坏小盘在上，大盘在下的规则。

3.移动好最大的盘后，就只需考虑剩下的n-1个盘，我们可以把第n-1个盘当成最大的盘，这样又回到了第2步，不过区别是将n-2借助target杆移动到start杆上，方便第n-1个盘从temp杆移到target杆。

4.以此类推，我们可以很清晰地理解hanoi递归过程。

代码如下：

#include <stdio.h>

void hanoi(int n, char start, char temp, char target)
{
	if (n == 1)
		printf("Move disk1 from %c to %c\n", start, target);
	else
	{
		hanoi( n - 1,  start,  target, temp);
		printf("Move disk%d from %c to %c\n", n, start, target);
		hanoi( n - 1,  temp,  target, start);
	}
}

int main(void)
{
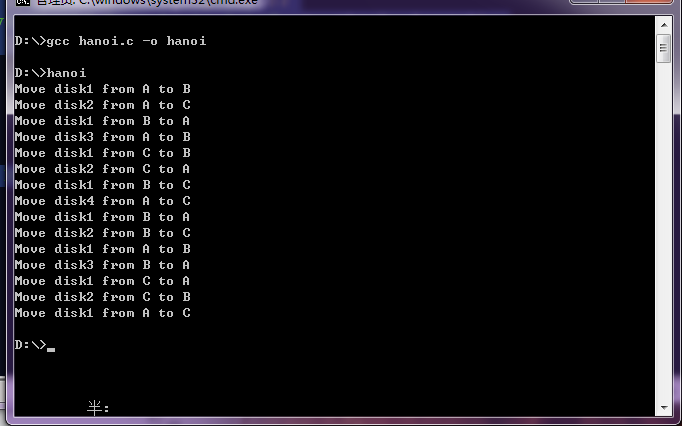
	hanoi(4, 'A', 'B', 'C');
	return 0;
}