机器学习 | 数学基础

机器学习的数学基础

作者:RichardsZ             公众号：智能驾驶软件宝典

本文简单整理了机器学习所涵盖的数学知识点，以结论的形式进行呈现，可作为便捷速查表，后续会继续进行完善！

---

前言

随着人工智能的不断发展，机器学习这门技术也越来越重要，很多人都开启了学习机器学习，本文就介绍了机器学习所需要的基本数学内容。

---

转载请注明出处，谢谢！

一、数列

一、矩阵

1. 矩阵的转置的转置仍为该矩阵，
    $(A^T{)}^T=A$
2. 矩阵相加的转置等于矩阵分别转置之后再相加。
    $(A+B{)}^T=A^T+B^T$
3. 标量乘矩阵的转置等于矩阵先转置后乘标量。
    $(\lambda A{)}^T=\lambda A^T$
4. 两个矩阵相乘的转置等于第二个矩阵的转置左乘第一个矩阵的转置。
    $(AB{)}^T=B^T\ast A^T$
5. 两个矩阵能够相乘的前提是，第一个矩阵的列数 = 第二个矩阵的行数，例如A为3x2的矩阵，B为2x4的矩阵，那么AxB为3x4的矩阵。
6. 单位矩阵，对角线上的元素为1，其它元素为0的矩阵。
7. 矩阵的逆，若AB=BA=E（E是单位矩阵），则称B是A的逆矩阵，而A则被称为可逆矩阵。
8. 如果一个行列式的两行（或两列）完全相同，那么这个行列式的值等于零 。
9.行列式计算常用方法：

计算方法
化三角形法
提公因式法	可根据矩阵的一行/一列提取元素，计算剩余行列式，如图下所示
9.矩阵的特征值和特征向量
–	–
特征值$\lambda$	计算行列式|$\lambda E-A$|,得到特征值$\lambda$
特征向量	将求得的特征值$\lambda$代入方程组$(\lambda E-A)x=0$,求得x向量

二、向量

1. 具有大小和方向的量。
2. 在表示向量的时候，各维度通常纵向书写$\left[\begin{array}{c}1\\ 4\end{array}\right]$，表示向量具备两个维度x和y，在x方向前进了1个单位，y方向上前进了4个单位。若用坐标表示，可体现为两个坐标点，如(0,0)->(1,4)，或(1,4)->(2,8)。
3. 向量的模 = 向量每个维度的平方开根号。如$\vec{x}$=$\left[\begin{array}{c}1\\ 4\end{array}\right]$,则$\Vert \vec{x}\Vert =\sqrt{1^2+4^2}$。
4. 零向量，模为0，方向任意。
5. 单位向量，模为1的向量，方向任意。
6. 向量标准化，向量的坐标分量除以向量的模长。
7. 向量的内积，为向量的模长的乘积再乘两个向量夹角的余弦值。若给出了坐标，向量内积等于对应分量乘积之和。$\vec{a}\cdot \vec{b}=\Vert \vec{a}\Vert \times \Vert \vec{b}\Vert \times cos\theta$
8. 向量的叉乘

10. 由向量的内积可推导出，柯西不等式，$\Vert \vec{a}\cdot \vec{b}\Vert <=\Vert \vec{a}\Vert \times \Vert \vec{b}\Vert$
11. $\Vert \vec{x}+\vec{y}\Vert <=\Vert \vec{x}\Vert +\Vert \vec{y}\Vert$
    10.向量的投影， 设两个非零向量$\vec{a}$与$\vec{b}$的夹角为θ，则将$\Vert \vec{b}\Vert \cdot cos\theta$叫做向量b在向量a方向上的投影或称标投影

三、L-P Norm(范数)

向量的范数
L-0 Norm(0-范数)	向量中非0元素的数量
L-1 Norm(1-范数)	也称曼哈顿距离，即两点在南北方向上的距离加东西方向上的距离，即$|x{|}_1={\Sigma }_{i=1}^n|x|$, 向量中的每个维度取绝对值进行加和
L-2 Norm(2-范数)	也称欧式距离，$|x{|}_2=\sqrt{{\Sigma }_{i=1}^n{x}_i^2}$,向量中的每个维度取绝对值进行加和
L-Infinity Norm(无穷范数)	向量中元素的最大值

四、微积分

1. 泰勒公式
    若函数$f(x)$ 在包含$x_0$的某个闭区间[a,b]上具有n阶导数，且在开区间(a,b)上具有(n+1)阶导数，则对闭区间[a,b]上任意一点x，下式成立：
    $f(x)=\frac{f(x_0)}{0!}+\frac{f^{\prime }(x_0)}{1!}\ast (x-x_0)+\frac{f^{\prime \prime }(x_0)}{2!}\ast (x-x_0{)}^2+\dots +\frac{f^{\prime n}(x_0)}{n!}\ast (x-x_0{)}^n+Rn(x)$
    其中，$Rn(x)$为泰勒公式的余项，$Pn(x)$，即除余项的部分为泰勒多项式。

2. 麦克劳林公式
    当$x_0=0$时，此时的泰勒多项式又称作麦克劳林公式。$f(x)=\frac{f(0)}{0!}+\frac{f^{\prime }(0)}{1!}\ast (x)+\frac{f^{\prime \prime }(0)}{2!}\ast (x{)}^2+\dots +\frac{f^{\prime n}(0)}{n!}\ast (x{)}^n+Rn(x)$
    例如$f(x)=ln(1+x)$，$f^{\prime }(x)=\frac{1}{1+x}$, $f^{\prime \prime }(x)=\frac{-1}{(1+x{)}^2}$
    将之代入麦克劳林公式：$ln(1+x)=0+x-\frac{x^2}{2!}+...+\frac{(-1{)}^{n-1}{x}^n}{n}+Rn(x)$

3. 函数的凹凸性
    设函数f(x)在区间I上定义，若对I中的任意两点x1和x2,和任意λ∈(0,1)，都有:
    $f(\lambda x_1+(1-\lambda )x_2)<=\lambda f(x_1)+(1-\lambda )f(x_2)$
那么这个函数为下凸函数(convex)，反之为下凹函数, 如下图所示。
    同时，也可以利用函数的二阶导数进行分辨：
     - 二阶导数>=0，随着自变量的增大，切线斜率越来越大，下凸函数；
     - 二阶导数<=0，随着自变量的增大，切线斜率越来越小，下凹函数；

Softmax

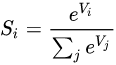
总结

    本文简单整理了机器学习所涵盖的数学知识点，以结论的形式进行呈现，可作为便捷速查表，后续会继续进行完善！
    转载请注明出处，谢谢！