“距离”、“范数”和范数正则化

1. 范数

先思考 机器学习中的行向量和列向量？

1.1 概念

向量的范数可以简单形象的理解为向量到零点的距离，或者相应的两个点之间的距离、或者向量的长度。

(如果对象是一个单独的向量，那么默认是指与原点进行比较，这情况下，范数代表的是向量到原点的距离，也就是向量的向量的长度；如果定义了两个向量，则范数可以表示这两个向量之间的距离）

1.2 定义

向量的范数定义：向量的范数是一个函数||x||，满足
非负性 ||x|| >= 0，
齐次性 ||cx|| = |c| ||x|| ，
三角不等式 ||x+y|| <= ||x|| + ||y||。

1.3 常见的向量范数

• L1范数: ||x||₁ 为x向量各个元素绝对值之和。

• L2范数: ||x||₂为x向量各个元素平方和的1/2次方，L2范数又称Euclidean范数或者Frobenius范数

• Lp范数: ||x||_p为x向量各个元素绝对值p次方和的1/p次幂

• L∞范数: ||x||_∞为x所有向量元素中的最大值（向量各个元素绝对值最大那个元素的绝对值），如下：

  

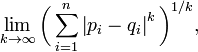
• 椭球向量范数: ||x||A = sqrt[T(x)Ax]， T(x)代表x的转置。定义矩阵C 为M个模式向量的协方差矩阵， 设C’是其逆矩阵，则Mahalanobis距离定义为||x||C’ = sqrt[T(x)C’x], 这是一个关于C’的椭球向量范数。

2. 距离

闵可夫斯基距离（对应 Lp 范数）

闵氏距离不是一种距离，而是一组 距离的定义。对应Lp范数，p为参数。

闵氏距离的定义：两个n维变量（或者两个n维空间点）X = (x₁, x₂, …, x_n) 与 Y = (y₁, y₂, …, y_n) 间的闵可夫斯基距离定义为：

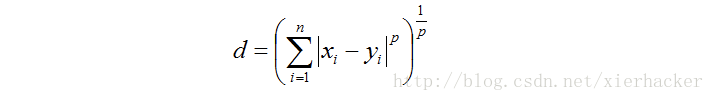
其中p是一个变参数。

当p=1时，就是曼哈顿距离，

当p=2时，就是**欧氏距离**，

当p→∞时，就是切比雪夫距离，       

根据变参数的不同，闵氏距离可以表示一类的距离。 

• 欧氏距离（对应 L2 范数）
• 曼哈顿距离（对应 L1 范数）
• 切比雪夫距离（对应 L∞范数）

汉明距离

分类特征的度量方式，比如比较字符串中相同字符的个数

Mahalanobis距离

Mahalanobis距离：也称作马氏距离。在近邻分类法中，常采用欧式距离和马氏距离。

3. 范数正则化

3.1 正则化的作用

• 防止模型过分拟合训练数据 <- 降低模型复杂度
• 约束我们的模型的特性 ->这样就可以将人对这个模型的先验知识融入到模型的学习当中，强行地让学习到的模型具有人想要的特性，例如稀疏、低秩、平滑等等。（人：大牛 ；模型：小白）

其它的角度看待正则化：

• 规则化符合奥卡姆剃刀(Occam’s razor)原理：在所有可能选择的模型中，我们应该选择能够很好地解释已知数据并且十分简单的模型
• 贝叶斯估计的角度：规则化项对应于模型的先验概率。
• 规则化是结构风险最小化策略的实现
  规则化风险 = 经验风险 + 正则化项/惩罚项

3.2 目标函数与正则化项

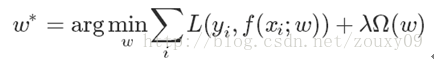
其实，线性回归应用L1正则项即为 Lasso 回归，应用L2正则项即为岭回归（Ridge Regression）。可以参考：点击

L0范数与L1范数

概念：

• L0范数是指向量中非0的元素的个数。
  如果我们用L0范数来规则化一个参数矩阵W的话，就是希望W的大部分元素都是0。换句话说，让参数W是稀疏的。
• L1范数是指向量中各个元素绝对值之和，也有个美称叫“稀疏规则算子”（Lasso regularization）。
  …
  L1范数和L0范数可以实现稀疏，L1因具有比L0更好的优化求解特性而被广泛应用。

补：

1. 为什么要稀疏？让我们的参数稀疏有什么好处呢？

• 特征选择(Feature Selection)

使用稀疏的一个关键原因在于它能实现特征的自动选择。它会学习地去掉没有信息的特征，也就是把这些特征对应的权重置为0。

• 可解释性(Interpretability)
  另一个青睐于稀疏的理由是，模型更容易解释。

2. L1是如何做到稀疏参数的？
   
   
   参考知乎上的两个回答：点击1、点击2

简单来说，如上面第一张图所示，明白下面几个点：
〇 横纵坐标是两个参数（以两个参数w₁和w₂来进行可视化举例）
① 蓝色圆圈部分为 不带正则项的情况，越靠里损失越小，越是最优解；
② 添加正则项相当于对参数进行了一个限制（将参数框定在黄色阴影部分），在图中体现是最优解必须是蓝色圆圈和下面黄色图形相切之处
③L1正则化和L2的差别是，使用L1正则项（右）会使得参数x₁=0（看第二张图），这就是“稀疏”的意思——两个参数x₁和x₂最后只剩下了x₂，n元参数同理。。。

更多可参考：点击

L2范数

除了L1范数，还有一种更受宠幸的规则化范数是L2范数: ||W||₂。它也不逊于L1范数，它有两个美称，在回归里面，有人把有它的回归叫**“岭回归”（Ridge Regression）**，有人也叫它“权值衰减weight decay”。

概念：
L2范数是指向量各元素的平方和然后求平方根。
原理：
我们让L2范数的规则项||W||₂最小，可以使得W的每个元素都很小，都接近于0，但与L1范数不同，它不会让它等于0，而是接近于0，这里是有很大的区别。（使用L1可以得到稀疏的权值，使用L2可以得到平滑的权值）
越小的参数说明模型越简单，所以通过L2范数，我们可以实现了对模型空间的限制，从而在一定程度上避免了过拟合。

好处：

• 学习理论的角度
  从学习理论的角度来说，L2范数可以防止过拟合，提升模型的泛化能力。
• 优化计算的角度
  从优化或者数值计算的角度来说，L2范数有助于处理 condition number 不好的情况下矩阵求逆很困难的问题。
  
  其他参考：
  

一句话小结：L2范数不但可以防止过拟合，还可以让我们的优化求解变得稳定和快速。

一句话总结：

L1会趋向于产生少量的特征，而其他的特征都是0，而L2会选择更多的特征，这些特征都会接近于0。
L1正则化产生稀疏模型，L2正则防止过拟合

更多参考 点击，值得好好理解学习！