【线代】线代基础知识回顾，SVD奇异值分解，Ax=0的解分析

一、首先要回顾以下线代一些基础知识：

1.向量的大小，也就是向量的长度（一般称作为 模），等于他和他自己的内积的平方根

2.若两个向量互相垂直，则两向量的内积为0。

3.正交矩阵：任何两行互相垂直，长度为 1，若一个方阵的行向量是正交的，则列向量都是正交的。正交矩阵的性质有，如正交矩阵A，A的转置等于A的逆。 可逆即满秩，反之满秩即可逆。正交矩阵的逆即其转置，当然可逆。可逆矩阵一定是方阵。可逆变换不改变秩。如3乘3的旋转矩阵就是正交矩阵，两个行向量的点乘为0，两个向量的叉乘为第三个行向量，每个行向量的模为1.

更多的正交变换和正交矩阵的性质参考这个链接：
https://blog.csdn.net/haoshan4783/article/details/90750469

4.对角矩阵：对角矩阵只在对角线上含有非0元素，其它位置都为0。

5.实对称矩阵：如果有n阶矩阵A，其矩阵的元素都为实数，且矩阵A的转置等于其本身（aij=aji）(i,j为元素的脚标)，则称A为实对称矩阵。（n行n列的矩阵是一个方阵，也叫做n阶矩阵），ATA 即矩阵乘自身的转置得到的就是实对称矩阵，更准确得说是半正定实对称矩阵，特别的，如果矩阵 A的列向量线性无关，那么他的特征值全部为正，即为正定矩阵。实对称矩阵中非零特征值的个数等于该矩阵的秩。
6.协方差矩阵：协方差矩阵就是实对称矩阵，因为实对称矩阵一定可以对角化，所以协方差矩阵也可以对角化，如下面第13条所说，对角化得到的特征向量控制旋转(rotation)，特征值控制尺度(scale)。得到了协方差矩阵的特征值和特征向量后，选择特征值最大(即方差最大)的k个特征所对应的特征向量组成的矩阵。这相当于只保留包含绝大部分方差的维度特征，而忽略包含方差几乎为0的特征维度，实现对数据特征的降维处理。协方差矩阵的最大特征值对应的特征向量，总是指向方差最大的方向；次最大特征值对应的特征向量，正交于最大特征值对应的特征向量，并指向次最大方差指向的方向。协方差矩阵的特征向量控制旋转(rotation)，特征值控制尺度(scale)
具体证明参见下图(下图中D为白数据，当数据协方差矩阵为单位阵时，该组数据被称为白数据，对白数据的概率分布做线性变换，线性变换矩阵为A，分解A就能得到R旋转矩阵和S尺度矩阵）和以下这个链接：

https://zhuanlan.zhihu.com/p/37609917

7.相似矩阵：相似矩阵的定义是，A、B都是n阶矩阵，若存在可逆矩阵P,使得P-1AP = B，(注意文中所有的P-1=P的逆矩阵)则定义矩阵B是矩阵A的相似矩阵或称矩阵A与矩阵B相似。对A 进行P-1AP称为对A进行相似变换。

8.矩阵的对角化：矩阵对角化：对n阶矩阵A，如果可以找到可逆矩阵P，使得P-1AP = 对角阵，就称为把方阵A对角化。注释：1、对角阵的主对角元素为A的特征值 2、可逆矩阵P由A的n个线性无关的特征向量作列向量构成。
矩阵对角化的充要条件：n阶矩阵有n个线性无关的特征向量。如果矩阵可以对角化，那么非0特征值的个数就等于矩阵的秩，如果不可以对角化结论就不一定了。 满秩的矩阵不一定有n个线性无关的特征向量。矩阵满秩的充要条件是矩阵的特征值都不为零（因为矩阵的行列式=所有矩阵特征值的累乘）。实对称矩阵一定可以对角化，因为实对称矩阵不同特征值的特征向量正交，n重特征值有n个线性无关的特征向量。因此实对称矩阵必然能够对角化。能够正交对角化的矩阵都是对称矩阵。（对角化就指的是相似对角化，如果是其他类型的对角化，比如正交对角化、合同对角化，一般会明说的。不加说明的话就是相似对角化），对实对称矩阵对角化的时候，正交单位化不是必须的，只有当我们想在实对称矩阵的诸多U里选取一个正交矩阵Q时，才需要做
矩阵的对角化相关知识点： https://blog.csdn.net/u011484045/article/details/44724369?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522166064706316782248513362%2522%252C%2522scm%2522%253A%252220140713.130102334…%2522%257D&request_id=166064706316782248513362&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2_blogsobaiduend~default-3-44724369-null-null.nonecase&utm_term=%E7%9F%A9%E9%98%B5%E5%AF%B9%E8%A7%92%E5%8C%96&spm=1018.2226.3001.4450
矩阵的对角化的计算过程：
https://blog.csdn.net/weixin_48524215/article/details/122634555?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522166148718216781432932223%2522%252C%2522scm%2522%253A%252220140713.130102334…%2522%257D&request_id=166148718216781432932223&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2_alltop_click~default-1-122634555-null-null.142^v42pc_rank_34_2,185^v2tag_show&utm_term=%E7%9F%A9%E9%98%B5%E5%AF%B9%E8%A7%92%E5%8C%96&spm=1018.2226.3001.4187

9.正定矩阵和半正定矩阵：如果A是实矩阵，则ATA（A的转置乘A）为实对称半正定矩阵。

正定矩阵的特征值全为正全大于0，而半正定矩阵的特征值是大于等于0，因为正定矩阵的行列式值为所有特征值的乘值，所以正定矩阵的行列式的值一定大于零。

10.特征值乘积等于对应方阵行列式的值，特征值的和等于对应方阵行列式对角线元素之和，n阶矩阵一定有n个特征值，因为特征值是特征多项式的根，n阶方阵的特征多项式|A-λE|是个n次多项式

11.属于同一个特征值的特征向量可能线性相关，也可能线性无关。 矩阵特征值相等时，特征向量的全体构成特征子空间，如果这个特征子空间的维数是1，那么所有的特征向量都是线性相关的。如果维数k大于1，那么必然存在k个线性无关的特征向量。判断特征子空间维数k只要看特征多项式中这个特征根的重数，是几重根，特征子空间的维数就是多少。

12. 如何判断向量组线性相关还是线性无关：若向量组的秩等于向量的个数，则该向量组是线性无关的；若向量组的秩小于向量的个数，则该向量组是线性相关的。具体做法就是先把向量组的各列向量拼成一个矩阵，并施行初等行变换变成行阶梯矩阵，若矩阵A秩小于向量个数m，方阵的情况下即叫不满秩行列式为0(矩阵的行秩和列秩相等），则向量组线性相关。行列式的性质中，如果行列式有两行（列）元素成比例，则此行列式为零。而组成方阵的各行（列）向量线性相关，只能说明方阵的某一行（列）可以由其他行线性表示。所以如果向量组的行列式为0，说明该向量组是线性相关的。所以可以引出的结论是一个矩阵的行向量里有多少个线性无关的向量，列向量里就一定也有多少个线性无关的向量

13.二次型的理解：二次型的表达式就是一个向量乘以一个实对称矩阵M再乘以前面那个向量的转置。二次齐次方程称为二次型，齐次方程是指简化后的方程中所有非零项的指数相等，二次齐次方程的意思是方程中每一项都是关于x、y的二次项。
下图这个齐次方程表示了一个圆

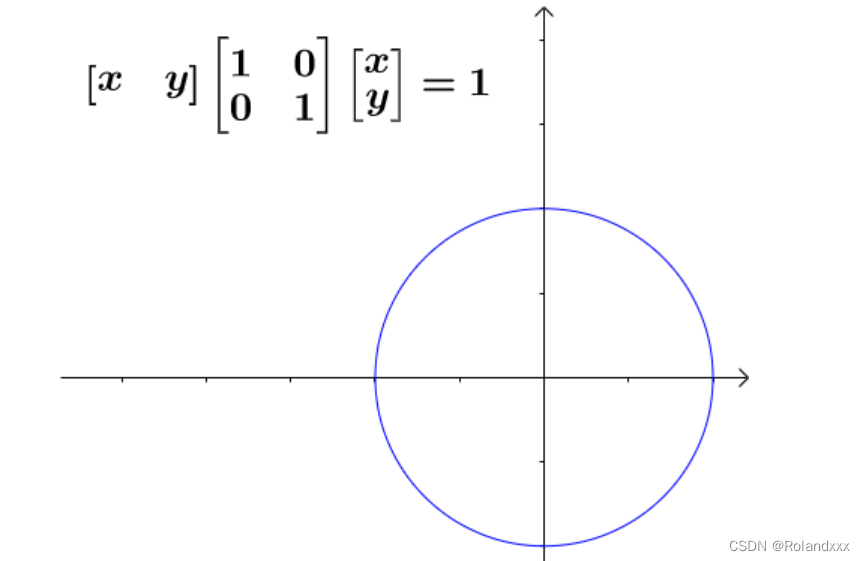
如果改变下二次型矩阵，把单位矩阵变成A矩阵，得到的图形如下所示，注意这里只有拉伸并没有旋转，因为把A矩阵分解后相当于左乘P-1，然后左乘对角矩阵，然后左乘P，旋转矩阵P-1和P抵消了：

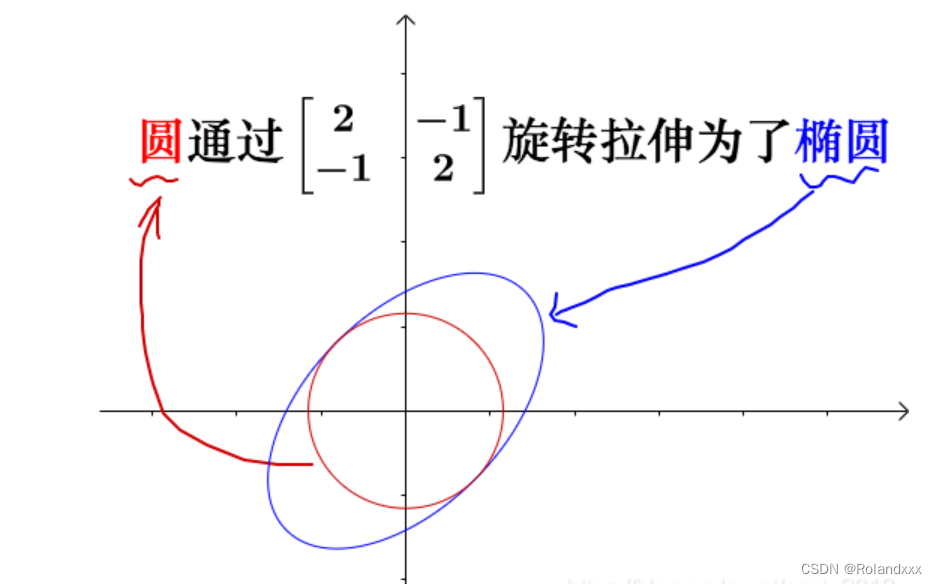
对矩阵A带来的形状变化的解释，因为矩阵代表了运动包含旋转拉伸和投影，而方阵因为没有维度的改变，所以就没有投影这个运动了只有旋转和拉伸。所以把二次型矩阵（对称矩阵）对角化实际上就是把运动分解了：

二次型在矩阵研究中的应用：https://matongxue.blog.csdn.net/article/details/84784311

二、SVD分解过程：

视频：
https://www.bilibili.com/video/BV1mx411E74T?p=6&vd_source=ec447224213be639260d3e28b04c224f

博客：
1.https://blog.csdn.net/weixin_44413191/article/details/108347942?ops_request_misc=&request_id=&biz_id=102&utm_term=%E7%9F%A9%E9%98%B5%E4%BB%BB%E4%BD%95%E4%B8%A4%E8%A1%8C%E4%BA%92%E7%9B%B8%E5%9E%82%E7%9B%B4&utm_medium=distribute.pc_search_result.none-task-blog-2_blogsobaiduweb~default-0-108347942.nonecase&spm=1018.2226.3001.4450
2.https://zhuanlan.zhihu.com/p/149674016

三、SVD奇异值的应用，求解求超定齐次线性方程组：Ax=0，Ax=b:

方法一：对矩阵 A做SVD 分解，分解后V 的最后一列向量即为Ax=0 的最小二乘解。
方法二：求解ATA 的特征向量和特征值，最小特征值对应的特征向量即为Ax=0 的最小二乘解。
注：L2范数可以省去下标2也就是右下角的2，左上角的2都代表平方，右下角的数字代表范数。

关于Ax = 0的求解，还有另一种理解，其实就是先看做Ax = λx，即特征值和特征向量的关系，x为特征向量，λ为特征值。当Ax = 0时，x肯定不为0因为x为0（0指向量而不是标量）就没有意义了，所以x就等于λ取0时对应的特征向量，通常我们是取λ最小时对应的特征向量为解但是极端情况下就是λ = 0时。原因如下：对于最小二乘法的对应的A，A等于UTU（U的转置乘U），得到的A是一个半正定实对称矩阵，所以特征值是大于等于0的，最小也就是最极端的情况下就是0，但我们在解的时候直接就是取特征值最小时对应的特征向量为解就行了。
参考链接（证明）：https://zhuanlan.zhihu.com/p/413247298

Ax=0, Ax=b的超定解的解法参照以下这个链接。超定方程组是指独立的方程组个数多于未知数，即当矩阵A行数大于列数时
https://blog.csdn.net/u011341856/article/details/107758182?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522166148758616782395348997%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=166148758616782395348997&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2_allfirst_rank_ecpm_v1~pc_rank_34-3-107758182-null-null.142^v42pc_rank_34_2,185^v2tag_show&utm_term=%E8%B6%85%E6%AD%A3%E5%AE%9A%E6%96%B9%E7%A8%8B%E7%BB%84&spm=1018.2226.3001.4187