例 7.2 训练数据与 例 7.1 相同。如图 7.4 所示,正实例点是 x 1 = ( 3 , 3 ) T x_1=(3,3)^T x1=(3,3)T, x 2 = ( 4 , 3 ) T x_2=(4,3)^T x2=(4,3)T,负例点是 x 3 = ( 1 , 1 ) T x_3=(1,1)^T x3=(1,1)T,试用 算法 7.2 求线性可分支持向量机。

算法 7.2 (线性可分支持向量机学习算法)
输入:线性可分训练集
T
=
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
⋯
,
(
x
N
,
y
N
)
T={(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)}
T=(x1,y1),(x2,y2),⋯,(xN,yN),其中
x
i
∈
χ
=
R
n
x_i \in \chi = \R^n
xi∈χ=Rn,
y
i
∈
Y
=
−
1
,
+
1
y_i \in Y = {-1,+1}
yi∈Y=−1,+1,
i
=
1
,
2
,
⋯
,
N
i = 1,2,\cdots,N
i=1,2,⋯,N;
输出:分离超平面和分类决策函数。
(1)构造并求解约束最优化问题
min
α
1
2
∑
i
=
1
N
∑
j
=
1
N
α
i
α
j
y
i
y
j
(
x
i
⋅
x
j
)
−
∑
i
=
1
N
α
i
s
.
t
.
∑
i
=
1
N
a
i
y
j
=
0
a
i
⩾
0
,
i
=
1
,
2
,
⋯
,
N
\begin{aligned} &\min_{\alpha} \dfrac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i\cdot x_j) - \sum_{i=1}^{N}\alpha_i \\ &~ s.t. \quad \sum_{i=1}^{N}a_iy_j=0 \\ &\quad \quad ~~a_i \geqslant 0, i=1,2,\cdots,N \end{aligned}
αmin21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)−i=1∑Nαi s.t.i=1∑Naiyj=0 ai⩾0,i=1,2,⋯,N
求解最优解
α
∗
=
(
α
1
∗
,
α
2
∗
,
⋯
,
α
N
∗
)
T
\alpha^*=(\alpha_1^*,\alpha_2^*,\cdots,\alpha_N^*)^T
α∗=(α1∗,α2∗,⋯,αN∗)T。
(2)计算
ω
∗
=
∑
i
=
1
N
α
i
∗
y
i
x
i
(
1
)
\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\omega^* = \sum_{i=1}^N \alpha_i^*y_i x_i \quad \quad\quad\quad\quad\quad(1)
ω∗=∑i=1Nαi∗yixi(1)
并选择
α
∗
\alpha^*
α∗的一个正分量
α
j
∗
>
0
\alpha_j^* >0
αj∗>0,计算
b
∗
=
y
j
−
∑
i
=
1
N
α
i
∗
y
j
(
x
i
⋅
x
j
)
(
2
)
\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad \quad \quad \quad \quad \quad \quad \quad b^* = y_j - \sum_{i=1}^N \alpha_i^* y_j(x_i \cdot x_j) \quad ~~ (2)
b∗=yj−∑i=1Nαi∗yj(xi⋅xj) (2)
(3)求得分离超平面
ω
∗
⋅
x
+
b
∗
=
0
\omega^* \cdot x + b^* = 0
ω∗⋅x+b∗=0
分类决策函数:
f
(
x
)
=
s
i
g
n
(
ω
∗
⋅
x
+
b
∗
)
f(x) = sign(\omega^* \cdot x + b^*)
f(x)=sign(ω∗⋅x+b∗)
在线性可分支持向量机中, 由式(1)、式(2)可知,
w
∗
w^*
w∗和
b
∗
b^*
b∗只依赖于训练数据中对应与
α
i
∗
>
0
\alpha_i^* > 0
αi∗>0 的样本点
(
x
i
,
y
i
)
(x_i,y_i)
(xi,yi),而其他样本点对
w
∗
w^*
w∗和
b
∗
b^*
b∗没有影响。我们将训练数据中对应于
α
i
∗
>
0
\alpha_i^* >0
αi∗>0 的实例点
x
i
∈
R
n
x_i \in \R^n
xi∈Rn 称为支持向量。
解
min
α
1
2
∑
i
=
1
N
∑
j
=
1
N
α
i
α
j
y
i
y
j
(
x
i
⋅
x
j
)
−
∑
i
=
1
N
α
i
=
1
2
(
18
α
1
2
+
25
α
2
2
+
2
α
3
2
+
42
α
1
α
2
−
12
α
1
α
3
−
14
α
2
α
3
)
−
α
1
−
α
2
−
α
3
s
.
t
.
α
1
+
α
2
−
α
3
=
0
α
i
⩾
0
,
i
=
1
,
2
,
3
\begin{aligned} &\min_{\alpha} \dfrac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i\cdot x_j) - \sum_{i=1}^{N}\alpha_i \\ &\quad\quad= \dfrac{1}{2}(18\alpha_1^2+25\alpha_2^2+2\alpha_3^2+42\alpha_1\alpha_2 -12\alpha_1\alpha_3-14\alpha_2\alpha_3) -\alpha_1-\alpha_2-\alpha_3 \\ & ~s.t. ~~ \alpha_1 + \alpha_2 - \alpha_3 = 0 \\ & ~\quad\quad \alpha_i \geqslant 0, i=1,2,3\\ \end{aligned}
αmin21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)−i=1∑Nαi=21(18α12+25α22+2α32+42α1α2−12α1α3−14α2α3)−α1−α2−α3 s.t. α1+α2−α3=0 αi⩾0,i=1,2,3
解这一最优化问题,将
α
3
=
α
1
+
α
2
\alpha_3 = \alpha_1 + \alpha_2
α3=α1+α2 代入木变函数并记为
s
(
α
1
,
α
2
)
=
4
α
1
2
+
13
2
α
2
2
+
10
α
1
α
2
−
2
α
1
−
2
α
2
s(\alpha_1, \alpha_2) = 4\alpha_1^2 + \dfrac{13}{2}\alpha_2^2 + 10\alpha_1\alpha_2-2\alpha_1-2\alpha_2
s(α1,α2)=4α12+213α22+10α1α2−2α1−2α2
对
α
1
,
α
2
\alpha_1,\alpha_2
α1,α2求偏导数并令其为0,易知
s
(
α
1
,
α
2
)
s(\alpha_1,\alpha_2)
s(α1,α2) 在点
(
3
2
,
−
1
)
T
(\dfrac{3}{2},-1)^T
(23,−1)T 取极值,但该点不满足约束条件
α
2
⩾
0
\alpha_2 \geqslant 0
α2⩾0,所以最小值应该在边界上达到。
当
α
1
=
0
\alpha_1 = 0
α1=0 时,最小值
s
(
0
,
2
13
)
=
−
2
13
s(0,\dfrac{2}{13}) = -\dfrac{2}{13}
s(0,132)=−132;当
α
2
=
0
\alpha_2=0
α2=0时,最小值
s
(
1
4
,
0
)
=
−
1
4
s(\dfrac{1}{4},0)=-\dfrac{1}{4}
s(41,0)=−41,于是
s
(
α
1
,
α
2
)
s(\alpha_1,\alpha_2)
s(α1,α2) 在
α
1
=
1
4
,
α
2
=
0
\alpha_1=\dfrac{1}{4},\alpha_2=0
α1=41,α2=0达到最小,此时
α
3
=
α
1
+
α
2
=
1
4
\alpha_3= \alpha_1+\alpha_2=\dfrac{1}{4}
α3=α1+α2=41。
此处使用MATLAB画出目标函数的曲面以及最小值点,如下图所示:
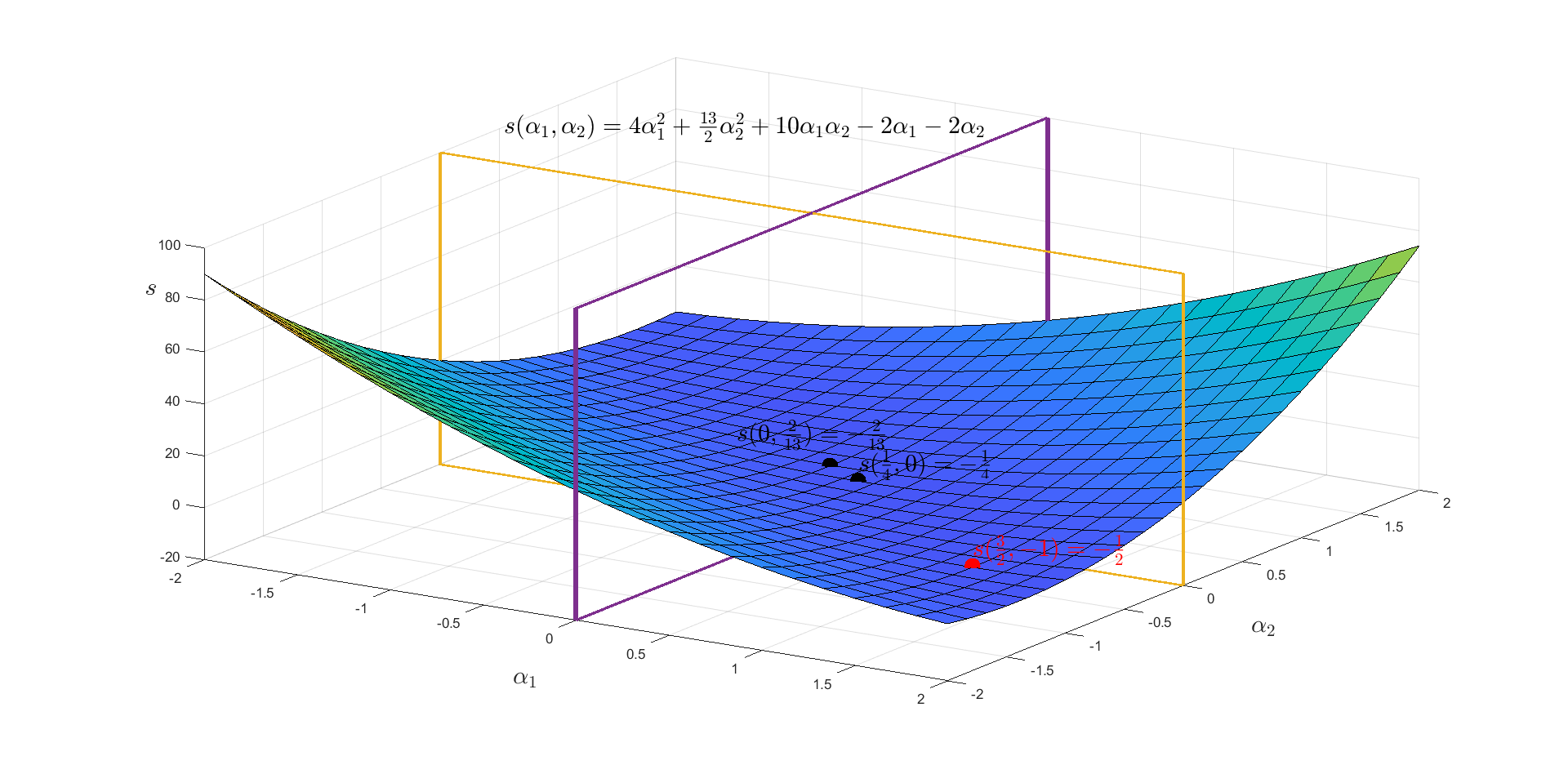
可以看出红色的点对应的 α 2 \alpha_2 α2值不满足 α i ⩾ 0 \alpha_i \geqslant 0 αi⩾0的约束条件,两个黑色的点分别为 α 1 = 0 , α 2 = 0 \alpha_1=0,\alpha_2=0 α1=0,α2=0 时与目标函数对于的曲面 s ( α 1 , α 2 ) s(\alpha_1, \alpha_2) s(α1,α2)相交的点。
可以得出
α
1
∗
=
α
3
∗
=
1
4
\alpha_1^*=\alpha_3^* =\dfrac{1}{4}
α1∗=α3∗=41对应的实例点
x
1
,
x
3
x_1,x_3
x1,x3是支持向量,根据式(1),式(2)计算可得
ω
1
∗
=
ω
2
∗
=
1
2
\omega_1^* = \omega_2^* = \dfrac{1}{2}
ω1∗=ω2∗=21
b
∗
=
−
2
b^*=-2
b∗=−2
分离超平面为
1
2
x
(
1
)
+
1
2
x
(
2
)
−
2
=
0
\dfrac{1}{2}x^{(1)} + \dfrac{1}{2}x^(2)-2=0
21x(1)+21x(2)−2=0
分类决策函数为
f
(
X
)
=
s
i
g
n
(
1
2
x
(
1
)
+
1
2
x
(
2
)
−
2
)
f(X) =sign(\dfrac{1}{2}x^{(1)}+\dfrac{1}{2}x^{(2)}-2)
f(X)=sign(21x(1)+21x(2)−2)
MATLAB可视化代码如下:
clc,clear
% 绘制曲面
x=linspace(-2,2,25);
y=linspace(-2,2,25);
[alpha1,alpha2]=meshgrid(x,y);
s=4*alpha1.^2+13/2*alpha2.^2+10*alpha1.*alpha2-2*alpha1-2*alpha2;
surf(alpha1,alpha2,s);
hold on
% 添加平面
% 添加竖线
[s,alpha2]=meshgrid(-20:0.1:100,-0.01:0.001:0.01);
alpha1=zeros(size(s))+2;
mesh(alpha1,alpha2,s,'FaceAlpha','0.9','EdgeColor',[0.9290 0.6940 0.1250]);
hold on
[s,alpha2]=meshgrid(-20:0.1:100,-0.01:0.001:0.01);
alpha1=zeros(size(s))-2;
mesh(alpha1,alpha2,s,'FaceAlpha','0.9','EdgeColor',[0.9290 0.6940 0.1250]);
hold on
[s,alpha1]=meshgrid(-20:0.1:100,-0.01:0.001:0.01);
alpha2=zeros(size(s))+2;
mesh(alpha1,alpha2,s,'FaceAlpha','0.9','EdgeColor',[0.4940 0.1840 0.5560]);
hold on
[s,alpha1]=meshgrid(-20:0.1:100,-0.01:0.001:0.01);
alpha2=zeros(size(s))-2;
mesh(alpha1,alpha2,s,'FaceAlpha','0.9','EdgeColor',[0.4940 0.1840 0.5560]);
hold on
% 添加横线
[alpha1,alpha2]=meshgrid(-2:0.1:2,-0.01:0.001:0.01);
s=zeros(size(alpha1))-20;
mesh(alpha1,alpha2,s,'FaceAlpha','0.9','EdgeColor',[0.9290 0.6940 0.1250]);
hold on
[alpha1,alpha2]=meshgrid(-2:0.1:2,-0.01:0.001:0.01);
s=zeros(size(alpha1))+100;
mesh(alpha1,alpha2,s,'FaceAlpha','0.9','EdgeColor',[0.9290 0.6940 0.1250]);
hold on
[alpha2,alpha1]=meshgrid(-2:0.1:2,-0.01:0.001:0.01);
s=zeros(size(alpha2))-20;
mesh(alpha1,alpha2,s,'FaceAlpha','0.01','EdgeColor',[0.4940 0.1840 0.5560]);
hold on
[alpha2,alpha1]=meshgrid(-2:0.1:2,-0.01:0.001:0.01);
s=zeros(size(alpha2))+100;
mesh(alpha1,alpha2,s,'FaceAlpha','0.01','EdgeColor',[0.4940 0.1840 0.5560]);
hold on
% 绘制点
Attribute_Set = {'LineWidth',1.5};
plot3(0,2/13,0,'.','MarkerSize',40,'Color','black');
plot3(1/4,0,0,'.','MarkerSize',40,'Color','black');
plot3(3/2,-1,0,'.','MarkerSize',40,'Color','red');
% 添加函数文本
text(-1.5,-0.25,120,'$s(\alpha_1,\alpha_2)=4\alpha_1^2+\frac{13}{2}\alpha_2^2+10\alpha_1\alpha_2-2\alpha_1-2\alpha_2$','interpreter','latex','FontSize',18);
% 添加坐标文本
text(-0.5,2/13,6,'$s(0,\frac{2}{13})=-\frac{2}{13}$','interpreter','latex','FontSize',18,'Color','black');
text(1/4,0,6,'$s(\frac{1}{4},0)=-\frac{1}{4}$','interpreter','latex','FontSize',18,'Color','black');
text(3/2,-1,6,'$s(\frac{3}{2},-1)=-\frac{1}{2}$','interpreter','latex','FontSize',18,'Color','red');
% 添加坐标轴标签
x1=xlabel('$\alpha_1$','interpreter','latex','FontSize',18); %x轴标题
x2=ylabel('$\alpha_2$','interpreter','latex','FontSize',18); %y轴标题
x3=zlabel('$s$','interpreter','latex','FontSize',18); %z轴标题
set(x1,'Position',[0.75,-3.5,0])
set(x2,'Position',[3,-1,0])
set(x3,'Position',[-2.3,-2,75])
set(x3,'Rotation',-8); %z轴名称旋转





















 7541
7541











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








