图论的基础

__Ryan<>

已于 2024-04-18 17:12:21 修改

阅读量879

点赞数 43

文章标签：图论

于 2024-04-18 16:25:53 首次发布

本文链接：https://blog.csdn.net/Ryan_hsMax/article/details/137603642

版权

本文详细介绍了图的基本概念，包括无向图、有向图、完全图、子图、带权图、连通性和强连通性，以及顶点的度数。还讲解了图的存储方式（邻接矩阵和邻接链表）和遍历方法（深度优先搜索和广度优先搜索），最后涉及欧拉路及其判断条件。

摘要由CSDN通过智能技术生成

图的基本概念

（1）无向图：每条边都是没有方向的。

如图：

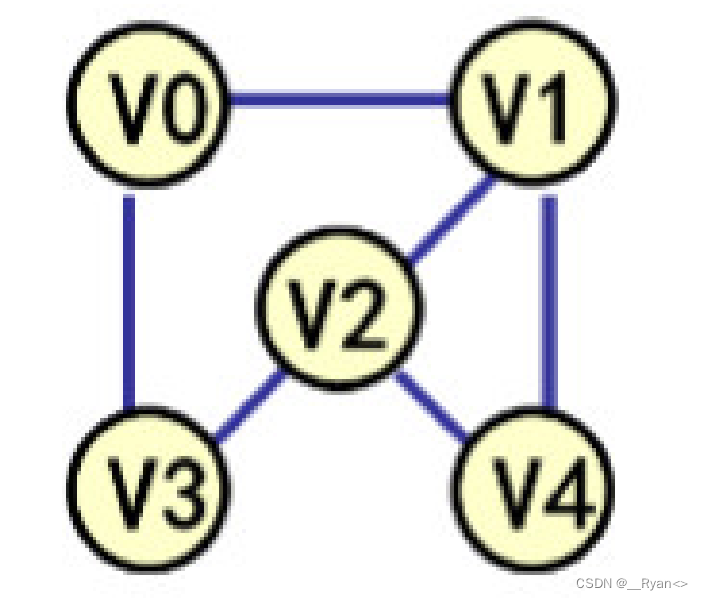
（2）有向图：每条边都是有方向的。

如图：

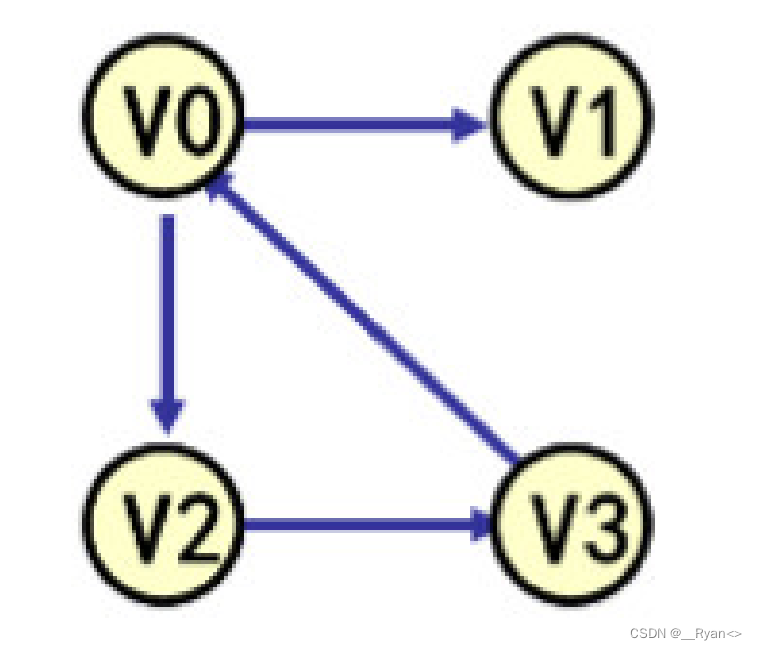
（3）完全图：任意两个顶点上都在一个边。

n个顶点的完全无向图有 n(n-1)/2 条边。
n个顶点的完全有向图有 n(n-1) 条边。
无向图 G 中顶点数为 n，则图 G 至少有 0 条边，至多有 n(n-1)/2 条边。
有向图 H 中顶点数为 n，则图 H 至少有 0 条边，至多有 n(n-1) 条边。

如图（可以自己数数呦；左边是完全无向图，右边是完全有向图）：

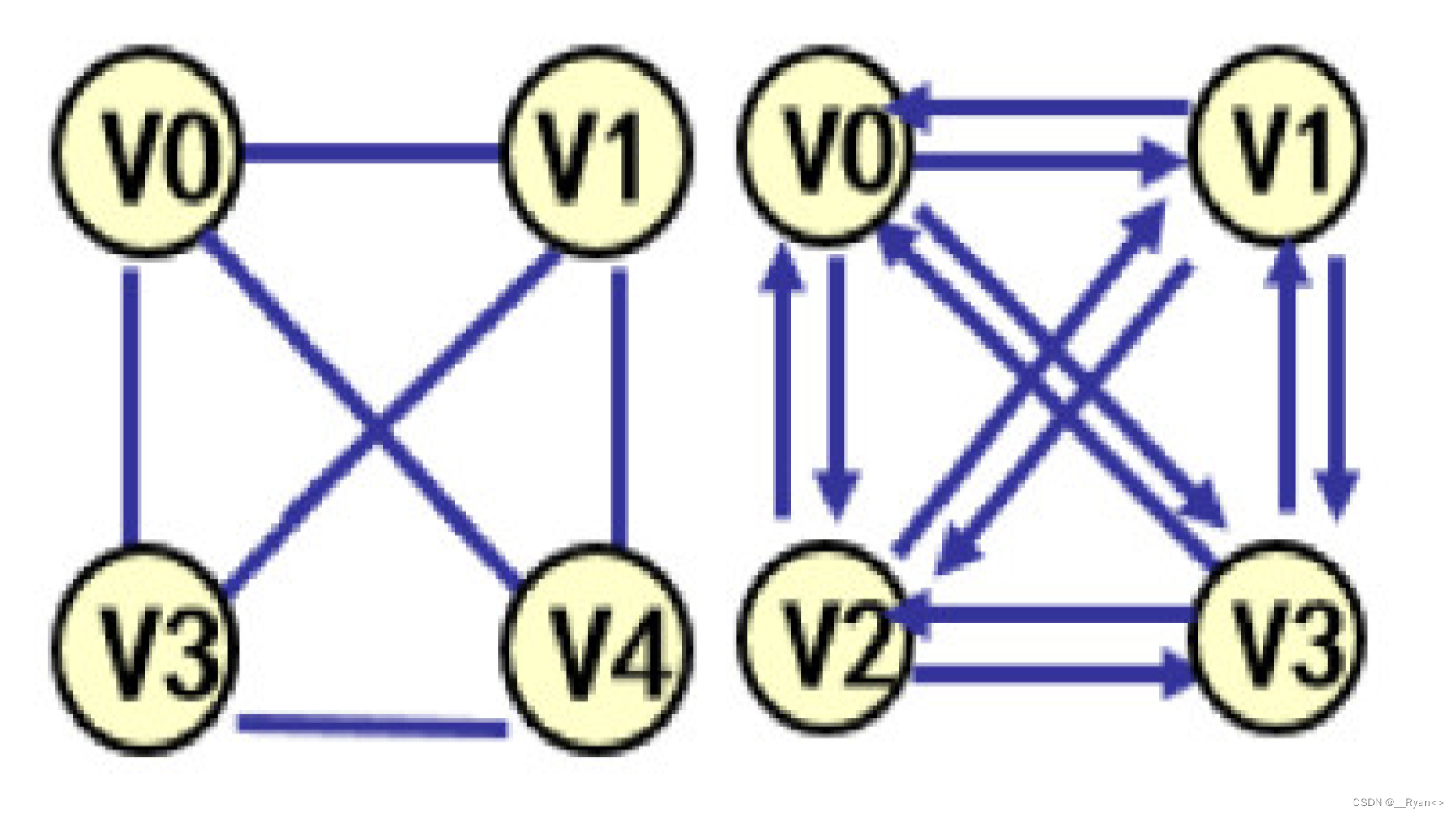
（4）子图：从图中取出的部分集合。

如图（1）：

如图（2）：

（5）带权图：边上带权的图（权：具有某种特殊含义的数值，如：表示两边之间的距离）。

如图：

（6）连通图：无向图中任意两个点都存在路径可达。

如图：

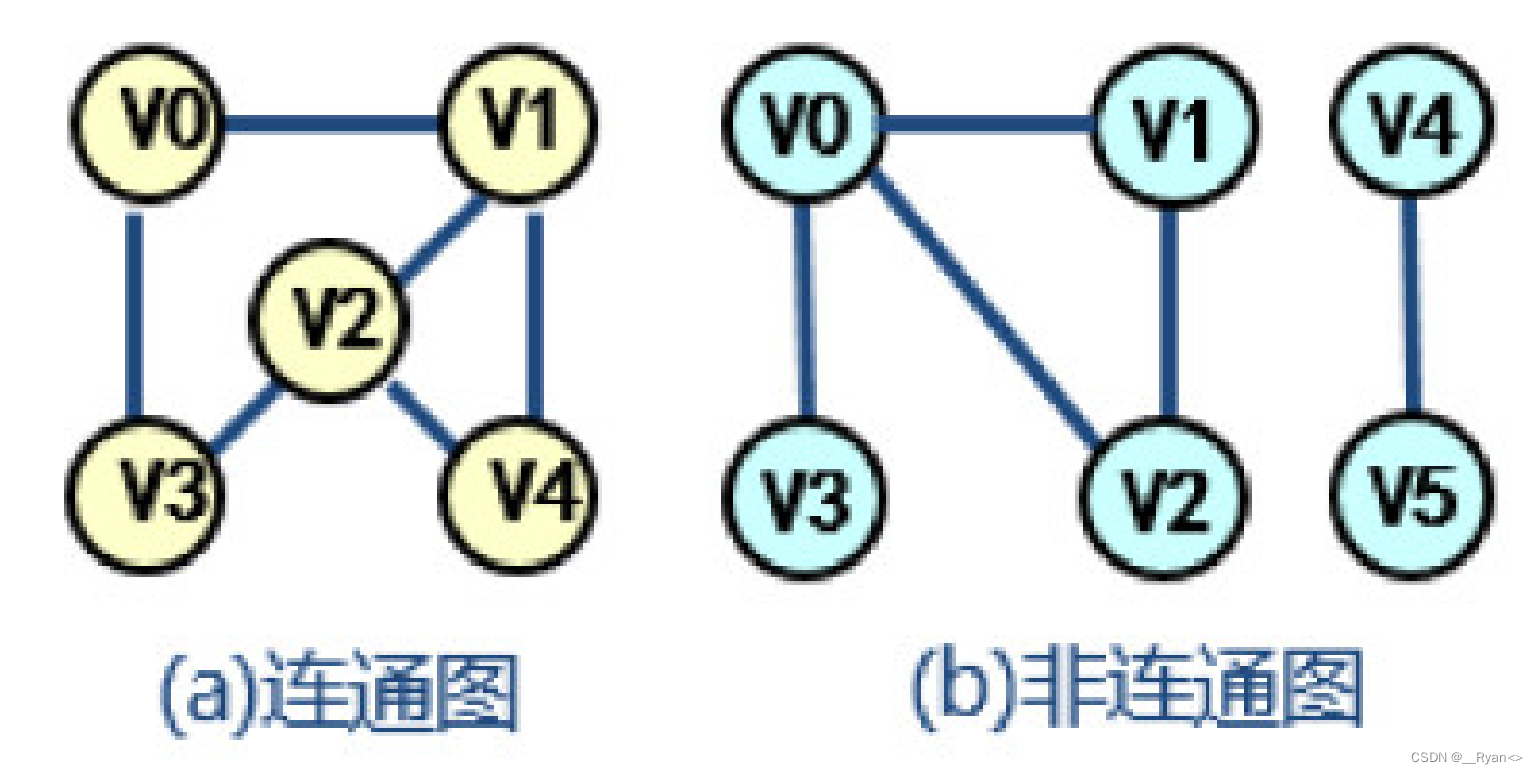
（7）强连通图：有向图中，若任意两个顶点都存在路径可达。

如图：

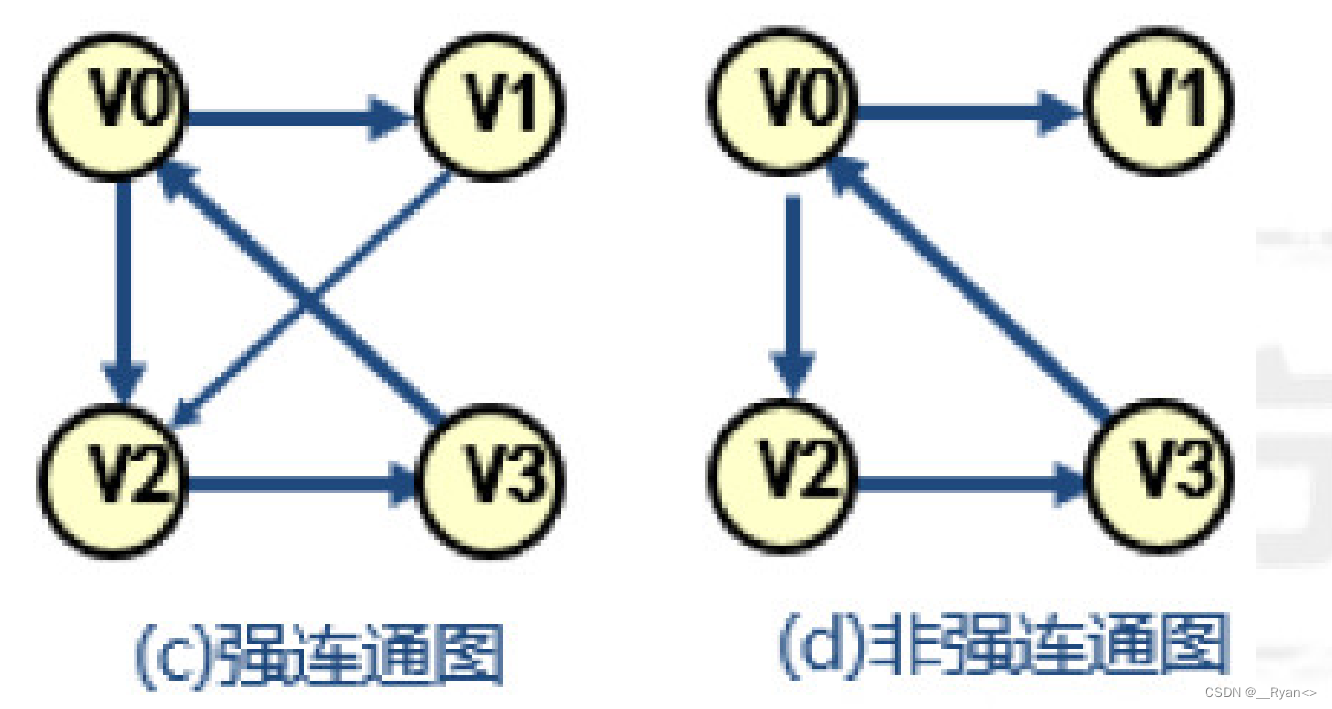
（8）顶点的度（有向图和带权图才有度）：与顶点有关的边的数目；

有向图分为出度与入度；
顶点V的出度=以V为起点有向的边数；
顶点V的入度=以V为终点有向的边数；
顶点V的度=V的出度+V的入度；
图的度=图中所有顶点度的和；

问题：一个图的顶点数为 n，边数为 e，则该图的度 = 2 * e 。

（9）路径与回路

路径：顶点 A 到顶点 B 的经过的所有的边；
简单路径：在一条路径中，除起点与终点以外，其余定点各不相同；
回路：起点和终点相同的路径；
简单回路：由简单路径组成的回路称为简单回路。

例题（答案在下面呦！）：在下图所示的无向图中：

（1）V0，V1，V2，V3 是不是简单路径？_______

（2）V0，V1，V2，V4，V1 是不是简单路径？_______

（3）写出无向图的一条简单回路________________

（4）写出有向图的一条简单回路________________

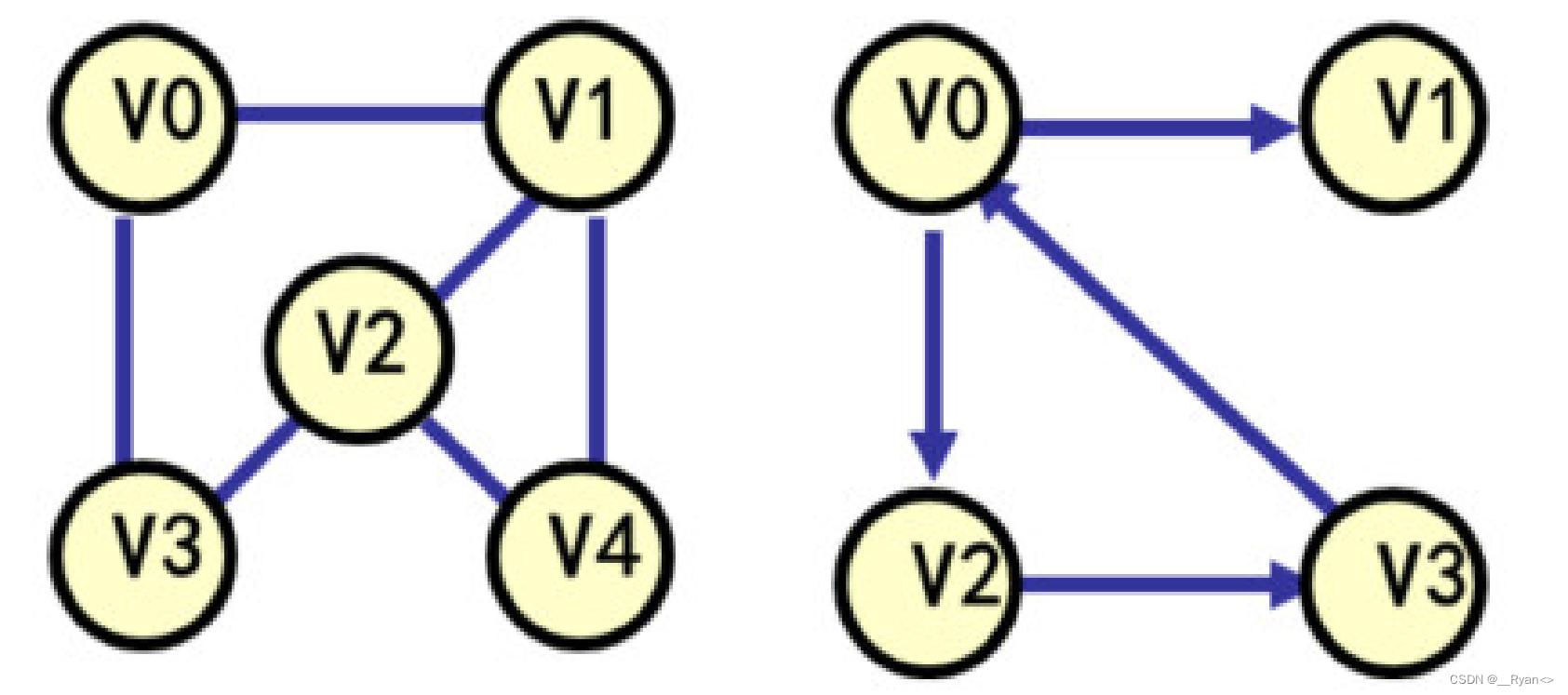答案：

（1）是。

（2）不是。

（3）V0，V1，V2，V3，V0。

（4）V0，V2，V3，V0。

（10）连通分量：在无向图中，如果从顶点 vi 到顶点 vj 有路径，则称 vi 和 vj 连通。如果图中任意两个顶点之间都连通，则称该图为连通图，否则将其中的较大连通子图称为连通分量。

在有向图中，如果对于每一对顶点 vi 和 vj ，从 vi 到 vj 和从 vj 到 vi 都有路径，则该图为强连通图；否则，将其中的极大连通子图称为强连通分量。

图的存储

1、邻接矩阵（数组）表示法

邻接数组表示法是以一个 n*n 的数组来表示一个具有 n 个顶点的图形。我们以数组的索引下（下标）值来表示顶点，以数组内容来表示顶点间边是否存在（1 表示存在，0表示不存在）。

例子：无向图的邻接矩阵：

如图：

根据上述无向图得到邻接矩阵，可以得到如下结论：

结论 1 ：无向图的邻接矩阵是对称的；

结论 2 ：顶点 i 的度=第 i 行（列）中 1 的个数；

注意：在完全图的邻接矩阵中，对角元素为 0，其余全是 1。

例子：有向图的邻接矩阵：

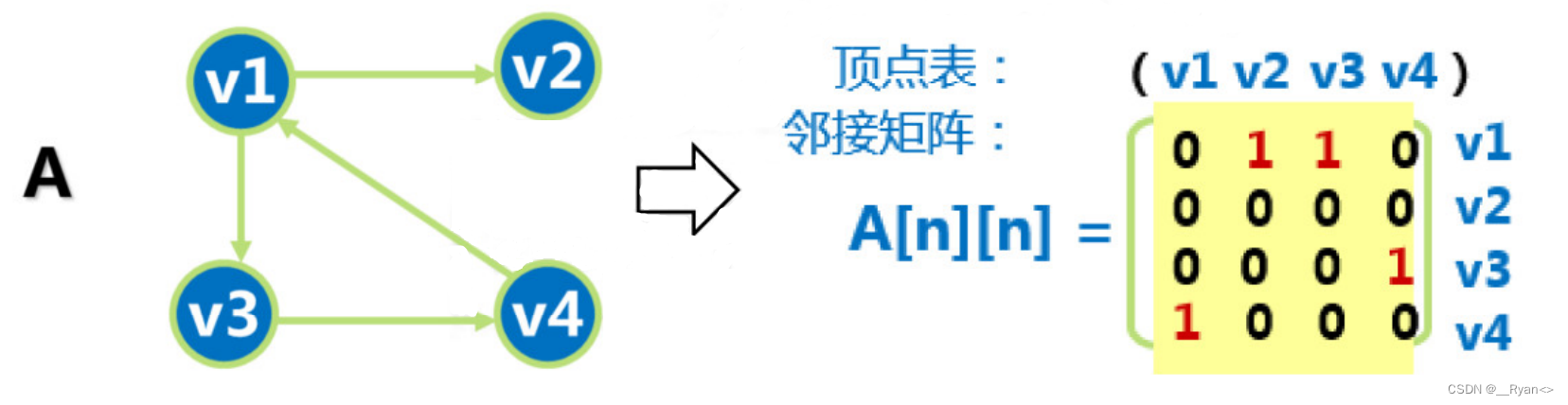
根据上述有向图得到邻接矩阵，可以得出如下结论：

结论 1 ：有向图的邻接矩阵可能是不对称的；

结论 2 ：顶点的出度 = 第 i 行元素之和；

顶点的入度 = 第 i 列元素之和；

图的度 = 矩阵中 1 的个数 * 2；

结论 3 ：图的存储空间占用量至于他的顶点数有关，与边数无关；适用于边比较稠密的图。

例子：带权图的邻接矩阵：

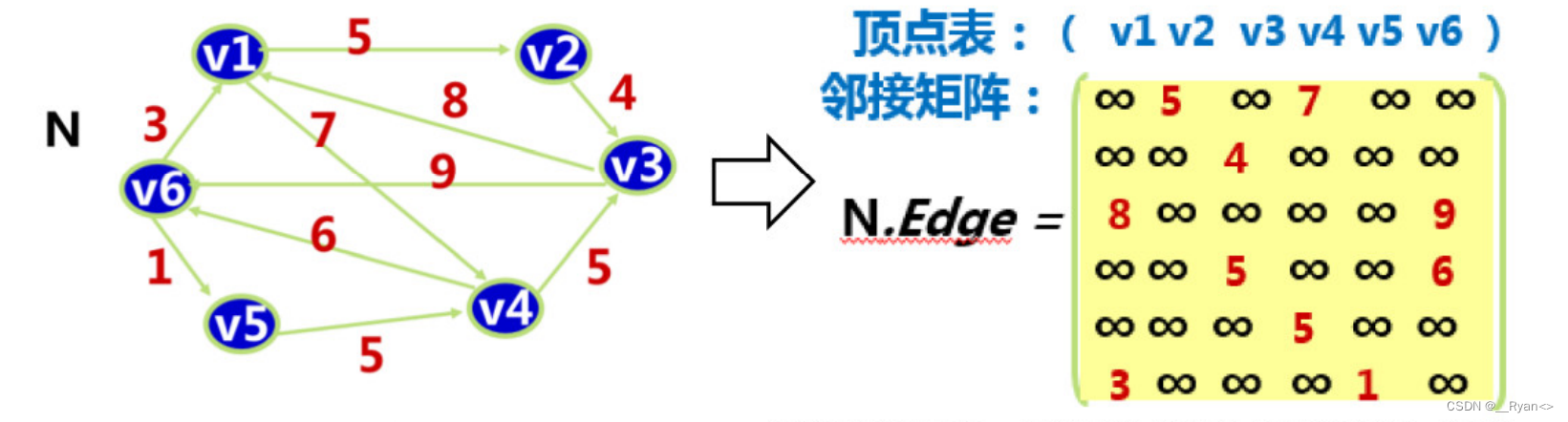
邻接矩阵的优点：容易实现图的操作，如：求某顶点的度、判断顶点之间是否有边（弧）、找顶点的邻接点等等。

邻接矩阵的缺点：n 个顶点需要 n*n 个单元存储边（弧）。对稀疏图而言，简直是在浪费空间！

2、邻接（链式）表的表示：

邻接链表法：以链表的方法来记录某个顶点的临界顶点。

例 1 ：无向图的邻接链表：

例 2 ：有向图的邻接链表：

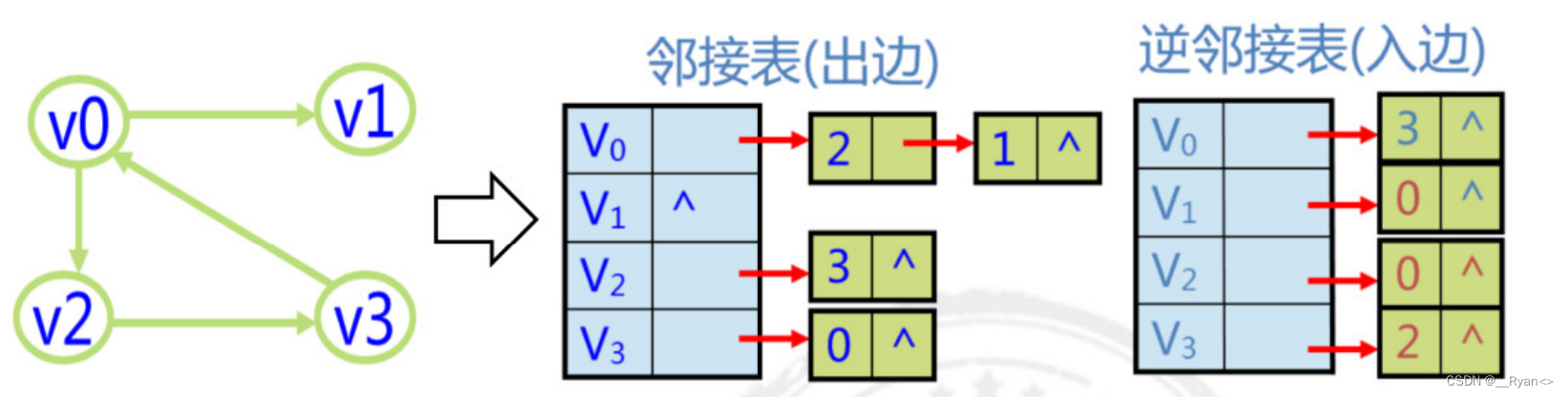
例 3 ：网（带权图）的邻接链表：

图的遍历

从图的某个顶点出发，访问图中的所有顶点，且使每个顶点仅被访问一次。这一过程叫做图的遍历。遍历方法：深度优先遍历和广度优先遍历。

1 . 深度优先搜索（DFS）

基本思想：——仿树的先序遍历过程。

步骤：

（1）访问起始点 v ；

（2）若 v 的第 1 个邻接点没访问过，深度遍历此邻接点；

（3）若当前邻接点已访问，再找 v 的第 2 个邻接点重新遍历；

代码如下：

#include<bits/stdc++.h>
using namespace std;
int a[20][20];
int n,e;
bool f[20];
void dfs(int x){
	f[x]=1;
	cout<<x<<' ';
	for(int i=1;i<=n;i++){
		if(a[x][i]==1&&!f[i]) dfs(i);
	}
}
int main(){
	cin>>n>>e;
	int x,y;
	for(int i=1;i<=e;i++){
		cin>>x>>y;
		a[x][y]=1;
		a[y][x]=1;
	}
	dfs(1);
	return 0;
}

2 . 广度优先搜索（BFS）

基本思想：——仿树的层次遍历过程。

步骤：

（1）在访问了起始点 v 之后，依次访问 v 的邻接点；

（2）然后再依次访问这些顶点中未被访问过的邻接点；

（3）直到所有顶点都被访问过为止；

注意：广度优先搜索是一种分层的搜索过程，每向前走一步都可能访问一批顶点，不想深度优先搜索那样有回退的情况。因此，广度优先搜索不是一个递归的过程，其算法也不是递归算法。

代码如下：

#include<bits/stdc++.h>
using namespace std;
int a[20][20];
int q[20];
int h,t;
int n,e;
bool f[20];
int main(){
	cin>>n>>e;
	int x,y;
	for(int i=1;i<=e;i++){
		cin>>x>>y;
		a[x][y]=1;
		a[y][x]=1;
	}
	h=1;
	t=1;
	q[1]=1;
	f[1]=1;
	cout<<1<<' ';
	while(h<=t){
		for(int i=1;i<=n;i++){
			if(a[q[h]][i]==1&&!f[i]){
				cout<<i<<' ';
				t++;
				q[t]=i;
				f[i]=1;
			}
		}
		h++;
	}
	return 0;
}

欧拉路——图的一笔画问题

1 . 基本概念

欧拉路指的是——存在这样一种图，可以从其中一点出发，不重复地走完其所有的边。

如果欧拉路的起点与终点相同，则称之为欧拉回路。

其实就是一笔将从起点经过所有边到达终点（欧拉路）和一笔将从起点经过所有边回到起点的路径（欧拉回路）

2 . 如何判断是否有回路

（1）无向图

结论：度数为偶数。

证明：为了形成回路，必定进入节点后，必须出去连接下一点（也就是说，进入节点多少次，就要出节点多少次）。

如果存在奇数条边，那么必定有一条边只可以进入节点，然而不可以出去和其它节点连接，就导致不可以构成回路。

（2）有向图

结论：出度与入度相等。

证明：同理，多少条边进入，就要多少条边出去。

3 . 判断是否有欧拉路径

欧拉路径与欧拉回路类似；

（1）在无向图中，除起点和终点是奇数条边，其余度数全都是偶数。

（2）除起点和终点以外，其余点出度与入度相等，起点出度比入度大 1 ，终点入度比出度大 1 。

总结：

（1）无向图能构成欧拉路：有 2 个或 0 个奇点；

（2）有向图能构成欧拉路：除起点和终点以外，其余点出度与入度相等，起点出度比入度大 1 ，终点入度比出度大 1 ，也可以出度=入度。

备注：当然，首要前提是——图是连通图。

欧拉路代码：

思路：

使用 DFS 寻找欧拉路的基本思想如下：

1 . DFS 寻找到第一个无边可走的结点，则这个结点必定为终点。

由于是 DFS 递归结束的时候记录的，那么该边是走完欧拉道路的最后的那条边，层层返回后最开始的也是最开始的出发地。

2 . 接下来由于 DFS 的递归回溯，会退回终点的上一个结点，继续往下搜索，直到寻找到第二个无边可走的结点，则这个接点必定是欧拉路中终点前最后访问的结点。

3 . 当通过 DFS 遍历完整张图之后，就可以倒序储存下整个欧拉路（因为是递归）。

如图：

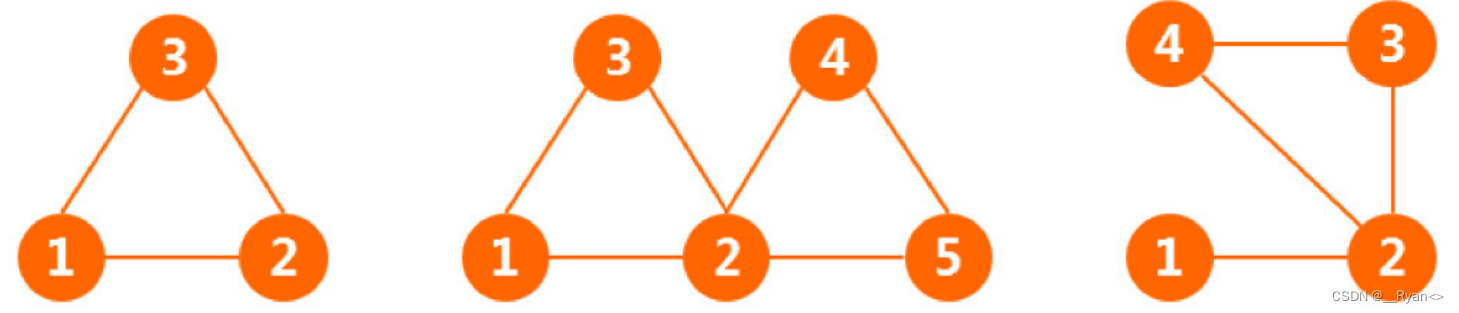
注意：防止是循环的方法是将走过的边都拆掉！

代码如下：

#include<bits/stdc++.h>
using namespace std;
int a[30][30];
int n,e;
int d[30];
int r[50];
int k;
void dfs(int x){
	for(int i=1;i<=n;i++){
		if(a[x][i]==1){
			a[x][i]=0;
			a[i][x]=0;
			dfs(i);
		}
	}
	k++;
	r[k]=x;
}
int main(){
	cin>>n>>e;
	int x,y;
	for(int i=1;i<=e;i++){
		cin>>x>>y;
		a[x][y]=1;
		a[y][x]=1;
		d[x]++;
		d[y]++;
	}
	int s=1;
	for(int i=n;i>=1;i--){
		if(d[i]%2==1){
			s=i;
			break;
		}
	}
	dfs(s);
	for(int i=k;i>=1;i--){
		cout<<r[i]<<' ';
	}
	return 0;
}