经典统计与贝叶斯统计介绍

梦断540

于 2024-08-29 12:23:03 发布

阅读量564

点赞数 22

文章标签：机器学习人工智能算法

本文链接：https://blog.csdn.net/SILVERCROWNAGE/article/details/141634316

版权

1. 经典统计

经典统计使用频率学派的方法，依赖于样本数据的频率分布进行推断。在经典统计中，参数被认为是固定但未知的，而推断过程主要是基于样本数据的统计性质进行。常见的经典统计方法包括置信区间、假设检验等。

思想：

从样本中直接观察频率，然后通过该频率来估计总体的参数。

2. 贝叶斯统计

贝叶斯统计使用贝叶斯学派的方法，将参数看作是一个随机变量，并使用先验分布和后验分布来进行推断。在贝叶斯统计中，参数的不确定性通过一个先验分布来表示，并通过样本数据更新为一个后验分布。常见的贝叶斯统计方法包括贝叶斯估计、贝叶斯因子等。

思想：

在先验的基础上，结合 “新数据”，给出未知参数。

优点：

在数据少的情况下可以进行推测，数据越多，推测越准确。对所获得的信息可以进行瞬时反应，自动升级的学习功能。

1. 先验概率

由 历史知因

先验概率是指在未考虑任何具体观测数据或新信息之前，对某个事件或假设发生的概率的估计。它是基于先前的经验、历史数据、专家判断或者其他背景知识来确定的概率。先验概率反映了我们对事件发生可能性的初始信念或不确定性。

例如：

测试在一次抛硬币实验时的正反面的概率：

在实验开始之前，我们无法给出其结果的概率分布，但是根据历史经验，我们假定正面向上的概率为 0.5，这个就是先验概率。

2. 后验概率

后验概率是在观察到某些数据或信息之后，对该事件或假设发生概率的修正后的估计。它是通过将先验概率与新的证据或数据相结合，利用贝叶斯定理计算得出的更新概率。后验概率更加反映实际情况，因为它考虑了新的证据影响。

例如：

对一个个体进行了测试并得到了阳性结果，那么根据这个测试结果以及已知该测试的灵敏度和特异性，可以计算出该个体实际患有该疾病的概率，这就是后验概率。

二者之间的区别与联系：

先验概率是基于先前的经验、历史数据、专家判断或者其他背景知识来确定的概率。后验概率是在观察到某些数据或信息之后，对该事件或假设发生概率的修正后的估计。先验概率的计算较为简单，不涉及贝叶斯公式的使用。后验则需要使用贝叶斯。
后验概率的计算依赖于先验概率，并且两者共同构成了贝叶斯统计推断的基础。通过贝叶斯公式，我们可以根据新的信息或数据对先验概率进行修正，得到更加准确的后验概率。

3. 似然概率

似然概率（likelihood probability）是指，在给定观测数据的条件下，所要推断的参数的取值出现的可能性。似然概率可以用来评估不同参数取值的可能性大小，并通过最大化似然概率来估计最有可能的参数取值。

似然概率与概率的区别在于，概率是在已知参数的情况下计算事件发生的概率，而似然概率则是在已知事件发生的情况下计算参数取值的可能性。

举个例子来说，假设有一枚硬币，我们想要估计它正面朝上的概率p。进行了10次独立的抛硬币的实验，结果有6次正面朝上。这里，似然概率是在已知有6次正面朝上的情况下，求p的取值可能性的函数。我们可以通过似然函数计算不同p取值下的似然概率，并找到使似然概率最大化的p值，从而估计硬币正面朝上的概率。

需要注意的是，似然概率本身并不是表示一个概率，因为它不一定满足概率的性质，例如总和为1。似然概率更多地用于参数估计和模型比较等统计推断中。

公式

公式：

$P(H|E) = \frac{P(E|H)*P(H)}{P(E)}$

P(H)是先验概率，P(H|E)是后验概率，P(E|H)/P(E)被称为调整因子，先验概率乘以调整因子就得到后验概率。

H表示Hypothesis（假设），E表示Evidence（证据），贝叶斯定理的意义就在于，给定一个先验概率P(H)，在出现了证据E的情况下，计算后验概率P(H|E)。

如果P(H)=0，则P(H|E)=0；如果P(H)=1，则P(E|H)=P(E)，P(H|E)=1。

也就是说，如果先验概率为0%或100%，那么，无论出现任何证据E，都无法改变后验概率P(H|E)。这对我们看待世界的认知有重大指导意义，因为贝叶斯概率的本质是信念，通过一次次事件，我们可能加强某种信念，也可能减弱某种信念，但如果信念保持100%或0%，则可以做到对外界输入完全“免疫”。

公式推导

由 $P(A\cap B) = P(A|B) * P(B) = P(B|A) *P(A)$

将左边的 P(A∩B) 去掉，则可得贝叶斯定理。

$P(H|E) = \frac{P(E|H)*P(H)}{P(E)}$

贝叶斯定理的另外一种表示

用P(H)表示H发生的概率，用H表示H不发生，P(H)表示H不发生的概率。显然P( $\bar{H}$ )=1-P(H)。

下图红色部分表示H，红色部分以外则表示H：

P(H)

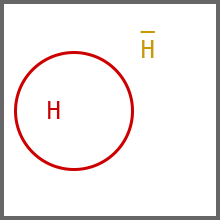
事件E用绿色表示：

P(E)

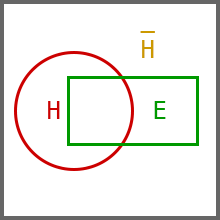
可见，P(E)可以分为两部分，一部分是E和H的交集，另一部分是E和H的交集：

P(E) = P(E∩H) + P(E∩ $\bar{H}$ )

根据上文的公式P(A∩B)=P(A|B)xP(B)，代入可得：

P(E) = P(E∩ $\bar{H}$ ) + P(E∩H)= P(E∣ $\bar{H}$ )×P( $\bar{H}$ ) + P(E∣H)×P(H)

把P(E)替换掉，我们得到贝叶斯定理的另一种写法：

$P(H|E) = \frac{P(E|H)*P(H)}{P(E|H)*P(H) + P(E|\bar{H}) * P(\bar{H})}$

用这个公式来计算，我们就不必计算P(E)了。

已知有一种疾病，发病率是0.1%。针对这种疾病的测试非常准确：

如果有病，则准确率是99%（即有1%未检出阳性）；
如果没有病，则误报率是2%（即有2%误报为阳性）。

现在，如果一个人测试显示阳性，请问他患病的概率是多少？

P(E|H)表示患病时检测阳性的概率=99%；
P(H)表示患病的概率=0.1%；
P(E|H)表示没有患病但检测阳性的概率=2%；
P(H)表示没有患病的概率=1-P(H)=99.9%。

代入公式，计算：

P(H∣E)=99%×0.1%+2%×99.9%99%×0.1%=0.04721=4.721%

假设这个人又做了一次检测，结果仍然是阳性，那么他患病的概率是多少？

我们仍然使用贝叶斯定理计算，只不过现在先验概率P(H)不再是0.1%，而是4.721%，P(E|H)和P(E|H)仍保持不变，计算新的P(H|E)：

P(H∣E)=99%×4.721%+2%×(1−4.721%)99%×4.721%=0.71=71%

结果为71%，两次检测为阳性的结果使得先验概率从0.1%提升到4.721%再提升到71%，继续第三次检测如果为阳性则概率将提升至99.18%。

可见，贝叶斯定理的核心思想就是不断根据新的证据，将先验概率调整为后验概率，使之更接近客观事实。