小学数学原理1：17-那些遗留的未知问题

摘要

本节作为小学数学原理课程的最后一课，总结了前阶段学习的知识点，并提出了遗留的未知问题。强调数学学习的最佳方法是模拟古代先祖发展数学的过程，理解数形结合的重要性。课程从数的分类、奇偶数、质数合数的概念入手，引出哥德巴赫猜想等高级数学问题。同时介绍了数轴模型，帮助理解加法、减法及混合运算的原理。最后，通过引入负数、小数和分数等概念，展示了数学在解决实际问题中的应用，鼓励学生主动思考，拓展数学知识网络。本课旨在引导学生从生活中寻找数学问题，主动探索数学奥秘。

课程介绍与总结方法

1.介绍课程内容：第一阶段课程的最后一课，总结已学过的知识点。
2.总结方法：不是总结公式和定理，而是基于原有知识点主动发现问题。
3.课程名称：那些遗留的未知问题。

数学发展的模拟过程

1.现代数学家观点：学好数学的最佳方法是模拟古代先祖发展数学的过程。
2.数学发展过程：通过已有知识发现新问题，不断发芽生长，形成树状结构。
3.数学知识来源：基于现有知识和实际情况，因新问题而产生。

数的分类

1.数的分类：包括奇偶数、质数合数、完全平方数。
2.数形结合：通过图形理解数字分类，如奇偶数的排列和质数合数的图形表示。
3.完全平方数：可以写成连续奇数之和。

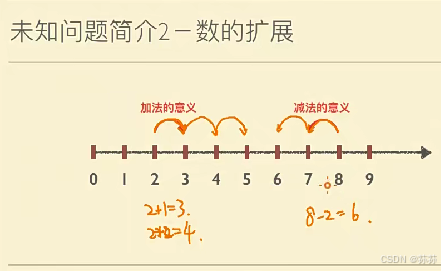
数轴与加减法

1.数轴定义：将数按照从小到大的顺序排列成一条线。
2.加法意义：合并操作，通过数轴上的移动表示。
3.减法意义：从总体中减去部分，通过数轴上的反向移动表示。
4.加法交换律和结合律：在数轴上解释其合理性。
5.减法交换律和结合律：在数轴上解释其合理性。
6.混合运算：加法和减法的混合运算，顺序不影响结果。

负数的引入

1.负数定义：小于零的数，表示向左的移动。
2.负数历史：数学家对负数的争议和接受过程。
3.负数应用：在温度计、支付宝、微信等生活中的应用。

新的运算扩展

1.乘法定义：简化大量相同数的加法运算。
2.乘法来源：解决大量人的学杂费计算问题。
3.除法定义：平均分配物品给多人。
4.除法应用：解决苹果平均分配问题。

小数和分数的扩展

1.小数定义：介于两个整数之间的数，如0.5或6.5。
2.小数应用：在超市标价牌、摄影快门速度中的应用。
3.分数定义：将单位1分成若干等份，如1/2或1/8。
4.分数应用：在音乐音符、摄影快门速度中的应用。

更高层次的扩展

1.比例定义：表示两个边长的比例，如16:9。
2.比例应用：在投影仪显示比例中的应用。
3.百分数定义：表示成分的比例，如50%的酒精浓度。
4.百分数应用：在饮料成分表中的应用。

之前的课程呢，我们都是每节课啊，讲一个小知识点，然后一点点向后推进，对吧？都是这么个节奏。但是今天的课程呢，会略有不同，因为是最后一节课呢，我们就稍微给大家总结一下。
我们基于现在的这些已经学过的知识点，你应该会有哪些问题？对我们今天的课程，虽说是总结课啊，但不是说向前总结，不是总结我们之前学过的哪些知识点啊，然后每一章有什么什么？呃，公式啊，有什么什么定理啊，不是这种总结，我们是一种更加高级的总结，就是你基于原来的那些知识点。你能不能向前去主动看到一些问题，对你看我们今天的课程题目啊，
叫那些遗留的未知问题。什么叫做遗留的未知问题呢？这个我需要跟大家稍微解释一下。一位现代的大数学家曾经说过。想要学好数学呢，其实最好的办法就是什么呢？并不是像大家想的，每天做很多试卷。被公式被定理，当然了，那些都是需要的，但是最最重要的一个因素是他说。需要我们在自己的头脑里完全模拟一遍我们古代的那些先祖如何把数学一点点发展壮大的这么一个过程。也就是说你脑子里啊，需要有一颗像这样一样的向上拓展的，
这么一个小芽儿，然后呢，你会根据已有的这些知识啊，比如说我们现在已有两片叶子。然后呢，你可以从这两片叶子中间发现一些新东西，然后继续发芽。然后比如说又发出两片叶子来呢，你又可以根据现在学的这些东西，又发现一些问题，然后继续这样发芽。这样发芽发的久了，你看这棵树啊，慢慢就会成为一个比较大的树状的形的结构。比如从这里发芽，
这里发芽，然后继续往上长，再发芽，再发芽，再发芽，然后每一个芽啊，它还会再发芽，再发芽，再发芽。其实我们的数学系统啊，也是这样一点点，然后生根发芽，然后发展壮大，变成我们现在的这种情况。就是希望大家明白一件事情，
所有新的数学知识的出现，并不是说呃别人凭空砸给你的，而是。基于我们现在的数学知识以及联系我们生活中的一些实际情况，因为一些问题新的问题而产生的。我们现在虽然学的知识还不多啊，你看我们学了什么东西，学了基本的数字数数对吧？学了基本的单位测量，还有学了基本的加法和减法，按理说啊，我们学的数学知识在小学课本里啊，仍然只是非常少的一部分知识。但是基于这些，我们现在已经能够主动看到一些问题了，
具体有哪些问题呢？我这边给大家。稍微的我们这节课是一个概述概述课，这节课不会讲很多知识点，但是我会给大家呃基于现在的知识去。以主动的引出一些新的问题，而这些问题会成为你今后学习高级数学知识的一个切入点。好，我们来看第一个问题啊，第一类问题。呃数的分类，什么叫数的分类呢？我们之前已经学过数数了，对吧？一二三四五六七八九十我们讲过了。
如何从这种啊？这种是最简单的，对吧？如何从原始人的这种小石子儿技术，刻痕技术，然后一步一步的发展出？这个数字我们讲了好几节课啊，什么进制位置，然后符号系统这种东西对吧？然后但是还没有完啊呃，一些对数字有深入思考的小朋友，现在应该有一些更加。对它下面还有一些东西啊，更加深入的问题了，数字跟数字之间啊。
它还是有一些不同的，什么不同呢ÿ