小学数学原理3：3-数轴、数的分类和简便运算

摘要

本节为数学课程讲解，重点围绕数轴、数的分类及简便运算进行深入解析。首先介绍了数轴的概念及其重要性，并通过数轴解释了加减法的另一种理解方式，即加法相当于向右走，减法相当于向左走。接着讲解了数的分类，包括整数与非整数、正负数以及质数与合数的概念和判定方法。通过具体例题，详细阐述了分类讨论思想在解决复杂数学问题中的应用。最后，介绍了快速判定一个数能否被二、三、五整除的方法，以及哥德巴赫猜想等相关数学知识，并提供了判断奇偶性、质数与合数的实用技巧。整个视频内容丰富，既巩固了基础知识，又拓展了数学思维。

数轴的概念和特性

1.数轴是一条直线，最左边是零，右边是自然数。
2.数轴能够反映出加减操作中无法体现的特性。
3.加法在数轴上表示为向右走，减法表示为向左走。
4.通过数轴，加法可以理解为一种运动。

数轴在加减法中的应用

1.通过数轴，可以解释所有加减混合运算。
2.二减五在数轴上表示为从二往左走五格。
3.当结果为负数时，可以继续往左走，引入负数概念。
4.负数在数轴上表示为零左边的点。

负数的引入和生活应用

1.负数表示零左边的数，可以扩展加减法的概念。
2.负数在生活中有实际应用，如电梯的负一楼、负二楼，气温计的负度数。

数轴在加减法中的扩展

1.引入数轴后，加减法可以变成其他描述方式。
2.通过数轴，可以理解加减法的不同含义。

数轴在加减法中的应用题

1.通过数轴解决加减法应用题，理解数的运动。
2.例题：小明在数轴上14这个点，每秒钟往左走两格，问五秒和十秒后的位置。
3.通过数轴和加减法运算，计算小明在数轴上的位置。

分类讨论思想在数轴中的应用

1.分类讨论思想在解决复杂问题时非常重要。
2.例题：在数轴上找一个点到点一和点五的距离相等，且到点一的距离是到点五的距离的三倍。
3.通过分类讨论，找出符合条件的点。

数的分类方法

1.整数和非整数的分类：整数在整点上，非整数在缝隙里。
2.正负数的分类：正数在零的右边，负数在零的左边，零既不是正数也不是负数。
3.按照是否在整点上分类：整数包括正整数、负整数和零，非整数包括小数和分数。

奇偶数的定义和判定

1.偶数：能被二整除的整数。
2.奇数：不能被二整除的整数。
3.奇偶数的图形解释：偶数成双，奇数成单。
4.奇偶数的数轴解释：偶数跨两格，奇数跨一格。
5.奇偶数的运算规律：偶加偶、偶减偶、偶乘偶结果为偶；奇加奇、奇减奇结果为偶；偶乘奇结果为偶；奇乘奇结果为奇。

质数和合数的定义及判定

1.质数：除了一和它本身以外，不再有其他因数的数。
2.合数：除了一和它本身以外，还有其他因数的数。
3.质数的判定方法：看是否只能写成一种形式。
4.合数的判定方法：看是否可以写成多种形式。
5.100以内的质数表：二、三、五、七、十一、十三、十五、十七、十九、二十一、二十三、二十五、二十七、二十九、三十一、三十三、三十五、三十七、三十九、四十一、四十三、四十七、四十九、五十三、五十九、六十一、六十七、七十一、七十三、七十九、八十三、八十九、九十七。

快速判定一个数能否被二三五整除的方法

1.被二整除：看个位是否为零或偶数。
2.被五整除：看个位是否为零或五。
3.被三整除：看每个位上的数字之和是否为三的倍数。

今天呢，给大家来复习一下，我们第四节课的内容啊，数轴数的分类和简便运算。我们呃，非常快的把这节课的内容给大家简单过一遍啊好。首先来看数轴这个概念啊，数轴这个概念呢，是我们在小学高年级慢慢就要涉及到的一种。呃，对于树的这个心理模型啊，为什么要有竖轴呢？其实它数轴这个东西能够反映出很多，我们在原来的那种加减操作中所反映不出来的一些特性。

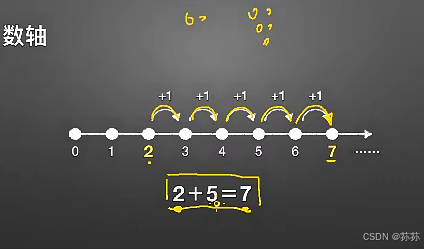
嗯，我们先把数轴给大家讲一下是什么东西，数轴就是这么一个东西是一条线。然后呢？最左边是零。一二三四五六七，这就是我们通常小学一开始学的自然数啊，我们就是把自然数呢，按照从左到右的这么一个顺序，排在一条整齐的线上。这就叫做数轴了，你可能觉得数轴是非常简单的一个东西，对吧？为什么要有它呢？原因是一旦有了数轴啊，
就像我刚才说的，我们能够对原来的一些基本运算有了另一个层次的理解。举一个最简单的例子加法。加法呢，原来我们怎么理解的？我们都是把合并对吧？把两堆东西，比如说一堆东西有这么多，一堆东西有这么多。然后把它合并到一起，问有多少呢？这个用加法来计算。但是一旦有了数轴啊，我们对加法有了第二种含义，它相当于是一种运动,加法相当于向右边走在数轴上啊，因为数轴一条线嘛，加法相当于向右走，减法相当于向左走。什么意思啊？通过一个例子给大家讲一下，比如说二+5=7。在数轴上表示它是什么意思呢？二我从二这个点开始走。加五是什么意思呢？往右走五格大家看啊，一格两格三格四格。五格走到了哪个点上呢？七所以二+5=7在数轴上，相当于是从二。往右边走，五格走到了七这个点，你看同样一种加法，运算不同的人，用不同的模型可以理解为完全不同的过程。所以以后我们在高年级做题的时候，你会发现哎，好像完全不同的题啊，但是最后做出来它们的式子完全一样。那这时候很多小朋友就就就犯难了，为什么呢？因为他们对于算式的理解太单一了，他只知道。两个球加五个球。
是二+5=7，却不知道在数轴上乱动，也可以做成二+5=7，这就会导致它某些题目做不出来。所以希望大家能够在呃我们学习数学的过程中啊，尽量能用不？那就是不同的，而且尽可能多的模型去解释同一个式子，换句话说，你对于同一个式子的理解，尽可能要非常多样化才行。那二加七是这个意思，比如说它反过来七减五等于二对吧？这个我们之前都会做七减五等于二，什么意思呢？就是从七这个点减嘛，往左走五下一二三四五。恰好走到二这个点，所以七减五等于二，它还可以表示混合运算啊，比如说七减。四+2等于几呢？我们来算算啊，七先往左走四格一。一二三四走到这里，对吧？再往右走，两格一二应该停在五。五我们看它是不是等于五啊七减四等于三三加二等于五确实等于五，所以这种方法确实可以解释一切加减混合运算。都可以在数轴上通过走来走出来。那通过引入数轴，还有另一个好处，就是它可以扩展我们对于加减法的概念。原来我们在加减法的时候都会遇到这种问题，会很疑惑，二减五等于几呀？貌似没法减啊，你如果问低年级的同学二减五等于几，他可能觉得你题出错对吧，但是一旦我们有了数轴。就不太难理解这个东西了，二减五的意义很明确，从二往左走五格。一格两格诶。
这才走两格呢，可是我已经到了最左边零了，这貌似是一个终点啊。那接下来该怎么办呢？这个时候数学界就会有两种呃观点，第一种观点是。这个式子不行，不能这么写，不成立，因为零就是最左边的东西了，不能再往前走。所以第一种数学家就认为这个式子有问题，不能写，而第二种数学家，他的思想就比较开放。他可能这么说，谁规定的零左边就不能走呢？我把这道门打开，继续往左走就是了，虽然我现在不知道是什么，但是我往那边去看看呀。看看，说不定就知道叫什么了，对吧？所以他们这些人认为还可以继续往左走。那二减五是什么意思呢？从二往左走，一格两格三格四格五格应该走到这个地方。可是这个地方叫什么呢？一开始人是不知道的，直到后来。看，这就是我们那个第二种数学家的想法，它从零又往左走了三个。那但是一开始我们不知道它叫什么，也不知道它的具体含义是什么意思，直到后来人们在生活中慢慢体会到了它的含义。它是什么意思呢？我们后来给给左边的这些数也命名了零的，左边第一个就叫负一，左边第二格就叫负二。左边第三格就叫负三，第四格就叫负四，你看它跟我们右边的这些数都是对称的。所以零啊变成了一个中间的点。
右边呢，都是正的，一二三四越来越多，左边呢，都是负的，负一负二负三负四越来越少。所以通过这个呃小数轴啊，我们就引入了一种新的数的概念叫做。复数这概念呢，在大家上五年级之后，第一课就会学了。好，这是我们通过数轴啊，把正负数给它引出来，你可能会问这个数字在生活里有用吗？
或者说我们在生活里能见到这种负的数吗？大家可以想一想有没有？其实是有的，其实是有的啊，比如说在哪里呢？在电梯，电梯。一楼下面是不是还有啊？什么负一楼负二楼，这就相当于地下室了，对吧？比如说还有什么地方呢？还有我们的温度计。我说的不是那种测体温的水银温度计啊，那种温度计呢，不会有负值，因为你发烧总不可能发成0度或者负1度吧，那就直接。那就直接变成冰棍了，对吧？呃，我说的这种温度计是测量气温的，测量天气的那种温度计，它这边呢会有0度，然后上面有1度两度，但是它下面还有啊。负1度负2度，我们在通常报天气预报的时候也会有负的度数，对吧？比如说徐州这边最冷的可能有零下负12度。你们看天气预报的时候会看到的啊，比如说如果再往北京或者东北东北那边可能会更冷啊，或者零下20度。零下30度可能都有可能，所以这个数字在生活中也会慢慢的用到它，是有实际的含义的。好，我们看看啊，通过引入一个数轴之后哦，原来的加减法可以变成一些其他的描述方式。希望大家能够看得懂啊，不能说我说三个球加两个球你会做，但是从三往右边走两格你就不会了。呃，这个显然是不行，
所以我们来看这一题啊。

小明在数轴上14这个点画一个数轴啊。14这个点每秒钟羊往左走两格。问，五秒的时候，它站在哪里？十秒的时