机器学习，朴素贝叶斯分类笔记（例子嘎嘎简单，草履虫都能学会）

机器学习笔记系列

可以从上至下按顺序看喔

• 回归笔记：机器学习-回归算法笔记
• 分类笔记：机器学习-分类算法笔记
• 神经网络笔记：机器学习-神经网络算法笔记

朴素贝叶斯

介绍

• 首先从名字开始解释，朴素贝叶斯中的“朴素”二字突出了这个算法的简易性。朴素贝叶斯的简易性表现该算法基于一个很朴素的假设：所有的变量都是相互独立的，假设各特征之间相互独立。
• 啥是条件独立性假设呢，用公式来说就是如果$P(A,B|C)=P(A|C)P(B|C)$，那么A，B之间就是在C这个条件下独立的，举个例子
  • A：熬夜
  • B：上课迟到
  • C：赖床
  • 在赖床的条件下想使得熬夜通过赖床来影响到上课迟到的概率为0，这就表示熬夜和上课迟到他俩之间是条件相互独立的，这就叫做A与B相互独立
• 贝叶斯呢就是贝叶斯公式啦

条件概率

• 条件概率：$P(B|A)$
• 意思就是在A的条件下，B发生的概率

先验概率与后验概率

• 假设有一个事件B，他是由事件A引起的，那么P(A)就是我们的先验概率

• 即在事件B发生之前，我们对事件A的概率的一个最初的判断

• 好，现在我们已知道事件B的概率，想知道事件A的概率，也就是条件概率P(A|B)

• 即在事件B发生后，我们重新对A的概率进行评估，这就是后验概率

• 举个例子

  • 我们出去买西瓜，在没摸到西瓜前，我们只看到了西瓜的外表，于是我们判断该瓜是不是好瓜的概率就是先验概率
  • 而当我们摸到西瓜后，我们通过敲击西瓜等一系列方法判断出了该瓜是好瓜或坏瓜后，我们再用我们已经得到的经验来判断该瓜是好瓜的概率，这就是后验概率

全概率公式与贝叶斯公式

• 全概率全概率，说的就是一个事件全部的概率加在一起的公式，我们可以用一个模型来推导出来
• 
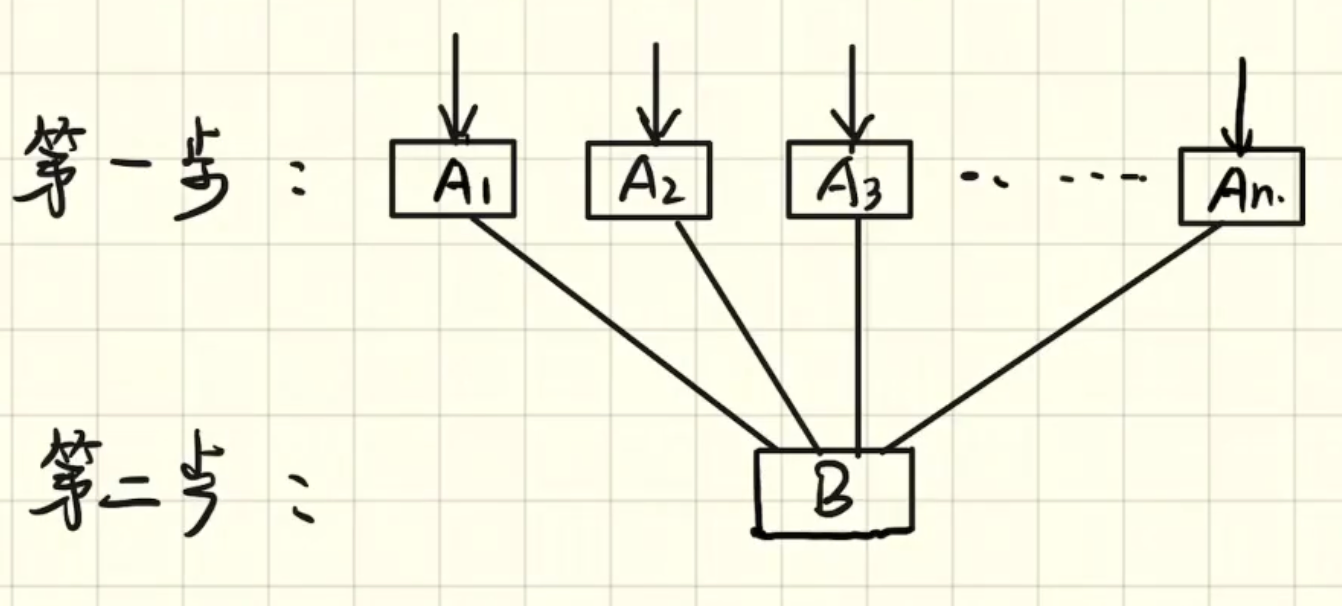
• 这是一个两步式模型，也就是第二步是由第一步得来的，可以看到有很多条路径A1、A2、、、An可以到达B
• 第一步我们取A1的概率就是P(A1)，第二步我们取B的概率就是P(B|A1)，也就是在A1完成的条件下B的概率
• 那么从A1这条路径完成B的概率是不是就是P(A1)P(B|A1)，那么第二条第三条路径也是同理

全概率公式

• 于是$P(B)=P\left(B\mid A_1\right)P\left(A_1\right)+P\left(B\mid A_2\right)P\left(A_2\right)+\dots +P\left(B\mid A_n\right)P\left(A_n\right)$
• 将各个通往B的路径的概率全部加在一起，这就是全概率公式
• 那贝叶斯公式是什么呢？贝叶斯是已知B，我们来求A1、A2或者An的概率，也就是用后验概率来推理先验概率，也就是求P(A1|B)或者P(A2|B)等等

贝叶斯公式

• 于是$P\left(A_i\mid B\right)=\frac{P\left(A_i\right)P\left(B\mid A_i\right)}{{\sum }_{j=1}^{n}P\left(A_j\right)P\left(B\mid A_j\right)}=\frac{P\left(A_i\right)P\left(B\mid A_i\right)}{P\left(A_1\right)P\left(B\mid A_1\right)+\dots +P\left(A_n\right)P\left(B\mid A_n\right)}$
• 贝叶斯公式也就是用一条路径的概率去除于所有路径的概率，举个例子
  • 我们有十条道路回家，那么随机选到第一条道路的概率是不是就是十分之一，也就是用这一条路的概率去除上所有回家的道路
• 最后我们将全概率公式与贝叶斯公式结合起来，就是：
  • $P\left(A_i\mid B\right)=\frac{P\left(A_i\right)P\left(B\mid A_i\right)}{P(B)}$

概率因子（可能性函数）

• 我们现在已经知道了贝叶斯公式：$P\left(A_i\mid B\right)=P\left(A_i\right)\frac{P\left(B\mid A_i\right)}{P(B)}$

• 我们将$\frac{P\left(B\mid A_i\right)}{P(B)}$部分叫做概率因子

• 于是我们可以得到如下几个推断：

  • 概率因子大于1时：意味着先验概率被增强，则事件A发生的可能性就会更大，也就是B有助于提高事件A的发生概率
  • 概率因子等于1时：意味着事件B对事件A发生的概率没有任何帮助
  • 概率因子小于1时：意味着先验概率被削弱，则事件A发生的可能性就会更小，也就是B减弱了提高事件A的发生概率

举个例子

• 我们有一个判断程序员是不是大佬的训练集，其中有十个样本，每个样本有三个特征

• 特征的选取范围如下

  • 数学：好、不好
  • 英语：好、不好
  • 代码能力：强、一般、弱

• 数学	英语	代码能力	是否大佬
  好	好	强	是
  不好	好	一般	不是
  不好	不好	弱	不是
  好	好	一般	是
  不好	好	强	是
  好	不好	一般	不是
  好	好	弱	是
  不好	不好	强	不是
  好	不好	强	是
  不好	好	弱	不是

• 现在给出一个特征为（数学好，英语不好，代码能力弱）样本，根据这个训练集，我们来判断这个样本是否是大佬

• 我们掏出贝叶斯公式：$P\left(A_i\mid B\right)=P\left(A_i\right)\frac{P\left(B\mid A_i\right)}{P(B)}$，将其转换一下：$P\left(类{别}_i\mid 特征\right)=P\left(类{别}_i\right)\frac{P\left(特征\mid 类{别}_i\right)}{P(特征)}$

• 根据这个公式，我们就可以计算是不是大佬的概率了

• 于是，是大佬的概率为：

  • $P\left(是\mid 数学好英语不好代码弱\right)=P\left(是\right)\frac{P\left(数学好英语不好代码弱\mid 是\right)}{P(数学好英语不好代码弱)}=P\left(是\right)\frac{P\left(数学好\mid 是\right)P\left(英语不好\mid 是\right)P\left(代码弱\mid 是\right)}{P(数学好英语不好代码弱)}$

• 不是大佬的概率为：

  • $P\left(不是\mid 数学好英语不好代码弱\right)=P\left(不是\right)\frac{P\left(数学好英语不好代码弱\mid 不是\right)}{P(数学好英不好代码弱)}=P\left(不是\right)\frac{P\left(数学好\mid 不是\right)P\left(英语不好\mid 不是\right)P\left(代码弱\mid 不是\right)}{P(数学好英语不好代码弱)}$

• 其中的$P(数学好英语不好代码弱)$为全概率公式，等价于：

  • $P(是)P\left(数学好\mid 是\right)P\left(英语不好\mid 是\right)P\left(代码弱\mid 是\right)+P(不是)P\left(数学好\mid 不是\right)P\left(英语不好\mid 不是\right)P\left(代码弱\mid 不是\right)$

• 然后我们分别计算一下上面的概率，对比一下就知道该样本是不是大佬了

  • $P(是)=\frac{1}{2},P(不是)=\frac{1}{2}$
  • $P(数学好|是)=\frac{4}{5},P(英语不好|是)=\frac{1}{5},P(代码弱|是)=\frac{1}{5}$
  • $P(数学好|不是)=\frac{1}{5},P(英语不好|不是)=\frac{3}{5},P(代码弱|不是)=\frac{2}{5}$

• 于是$P\left(是\mid 数学好英语不好代码弱\right)=\frac{\frac{1}{2}\frac{4}{5}\frac{1}{5}\frac{1}{5}}{\frac{1}{2}\frac{4}{5}\frac{1}{5}\frac{1}{5}+\frac{1}{2}\frac{1}{5}\frac{3}{5}\frac{2}{5}}=0.4$

• 同理可得$P\left(不是\mid 数学好英语不好代码弱\right)=0.6$

• 因为0.6>0.4，所以朴素贝叶斯算法预测该人不是大佬

朴素贝叶斯模型

多项式模型

• 多项式模型的特点为重复的词视其出现了多次
• 例如：
  • $P(数学，数学，英语，英语，代码|是)=P(数学|是)P(数学|是)P(英语|是)P(英语|是)P(代码|是)=P^2(数学|是)P^2(英语|是)P(代码|是)$
  • 可以看出多项式模型的思路和我们思维是一样的，在上述例子当中，“数学”，“英语”出现了两次，所以利用条件独立性，自然需要乘上两次

伯努利模型

• 伯努利模型与多项式模型刚好相反，它则视重复出现的词为一次
• 例如：
  • $P(数学，数学，英语，英语，代码|是)=P(数学|是)P(数学|是)P(英语|是)P(英语|是)P(代码|是)=P(数学|是)P(英语|是)P(代码|是)$
  • 伯努利则是无论出现了几次，均算其只出现了一次

高斯模型

• 高斯模型就是服从正态分布的朴素贝叶斯
• 正态分布公式：$P\left(X_j=x_j\mid Y=C_k\right)=\frac{1}{\sqrt{2\pi {\sigma }_k^2}}\exp \left(-\frac{{\left(x_j-{\mu }_k\right)}^2}{2{\sigma }_k^2}\right)$
• 其中$C_k$是第k个类别，$x_j$是第j个样本，${\mu }_k$和${\sigma }_k$是训练集的均值和方差

平滑处理

• 什么是平滑处理，我们用一个例子来说明一下平滑处理
• 还是拿上面那个例子，假设我们给数学特征的选择范围变成：好、一般、不好
• 而上面那个表格只是训练集，相当于数学一般的样本可能在测试集当中，碰巧没有加进来
• 且此时我们要预测的样本为（数学一般，英语好，代码能力强）
• 这个时候我们再用贝叶斯公式来计算是大佬的概率：
  • $P\left(是\mid 数学一般英语好代码强\right)=P\left(是\right)\frac{P\left(数学一般英语好代码强\mid 是\right)}{P(数学一般英语好代码强)}=P\left(是\right)\frac{P\left(数学一般\mid 是\right)P\left(英语好\mid 是\right)P\left(代码强\mid 是\right)}{P(数学一般英语好代码强)}$
• 当我们在训练集中计算$P(数学一般|是)$这个概率的时候发现是为0的，因为我们在训练集中根本找不到数学一般这个样本，所以其概率自然为0，这样一算，由于它是0，所以整个乘积也就为0了
  • 于是$P\left(是\mid 数学一般英语好代码强\right)$的概率则就变成0了，只是因为训练集没有该样本不代表数据集就没有，这明显是不对的，所以此时我们要引入平滑处理这个概念
• 引入平滑处理后公式为：$P\left(A_i\mid B\right)=\frac{P\left(A_i\right)P\left(B\mid A_i\right)+\alpha }{P(B)+n\alpha }$
• 其中的alpha就是平滑值，当alpha=1时为拉普拉斯平滑，n是特征的个数
• 一般朴素贝叶斯所采用的都是拉普拉斯平滑
• 经过平滑处理后，即使我们的训练集当中没有要测试样本的特征，则最后算出来的值也依然不为0
• 此时我们再预测刚刚所说的样本就能得出结果了，计算如下
  • $P(是)=\frac{1}{2},P(数学一般|是)=\frac{1}{8},P(英语好|是)=\frac{5}{8},P(代码强|是)=\frac{4}{8}=\frac{1}{2}$
  • $P(不是)=\frac{1}{2},P(数学一般|不是)=\frac{1}{8},P(英语好|不是)=\frac{3}{8},P(代码强|不是)=\frac{2}{8}=\frac{1}{4}$
  • 则$P\left(是\mid 数学一般英语好代码强\right)=\frac{\frac{1}{2}\frac{1}{8}\frac{5}{8}\frac{1}{2}}{\frac{1}{2}\frac{1}{8}\frac{5}{8}\frac{1}{2}+\frac{1}{2}\frac{1}{8}\frac{3}{8}\frac{1}{4}}=\frac{10}{13}\approx 0.77$
  • 而不是大佬的概率同上计算
  • 为$P\left(不是\mid 数学一般英语好代码强\right)=\frac{\frac{1}{2}\frac{1}{8}\frac{3}{8}\frac{1}{4}}{\frac{1}{2}\frac{1}{8}\frac{5}{8}\frac{1}{2}+\frac{1}{2}\frac{1}{8}\frac{3}{8}\frac{1}{4}}=\frac{3}{13}\approx 0.23$
• 因为0.77 > 0.23，所以该样本是大佬