机器学习，神经网络算法笔记（草履虫都能看懂），简单的一批

机器学习笔记系列

可以从上至下按顺序看喔

• 回归笔记：机器学习-回归算法笔记
• 分类笔记：机器学习-分类算法笔记

有监督学习

含义

• 给算法一个数据集，其中包含了正确的答案，告诉算法啥是对的啥是错的

• 我们想要在监督学习中，对于数据集中的每个样本，我们想要算法预测，并得出正确答案

神经网络

人工神经元

• 
• 上图中的x0是“偏置单元”， 上图名称为“带有sigmoid激活函数的人工神经元”，且为单个神经元
• 激活函数：像sigmoid函数等一些非线性函数的别称
• x为我们的输入单元，theta为我们的参数（权重）

神经网络

• 神经网络是由多个神经元所构成的，如下图所示

• 

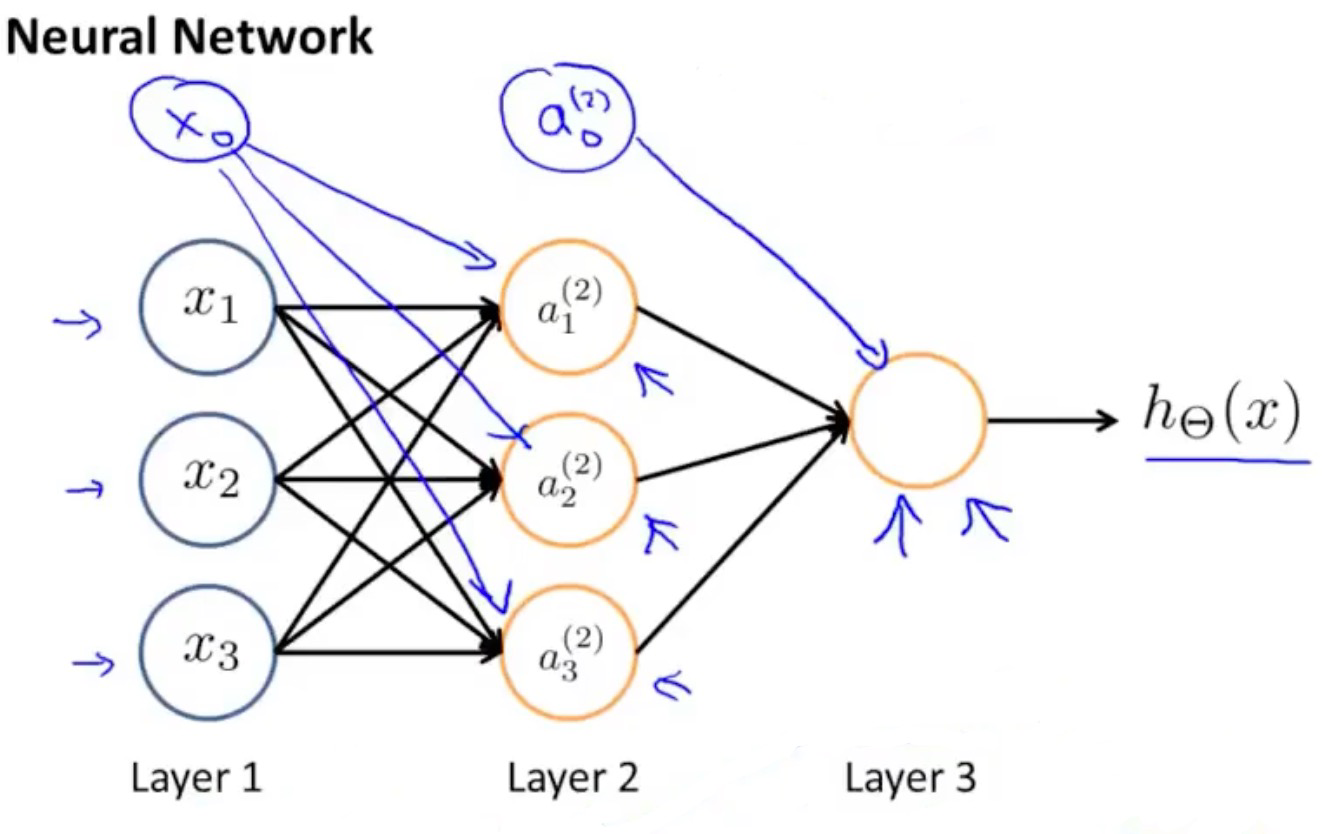
• 其中的层一为输入层，层二为隐藏层，层三为输出层

• 为什么叫隐藏层？

  • 因为该层的值在训练集里是看不到，所以叫隐藏层
  • 一个神经网络可拥有多个隐藏层，实际上除了输入层与输出层以外的都叫隐藏层

• 既然隐藏层的值在训练集看不到，可以通过以下计算出隐藏层的值

  • $a_1^{(2)}=g({\Theta }_{10}^{(1)}{x}_0+{\Theta }_{11}^{(1)}{x}_1+{\Theta }_{12}^{(1)}{x}_2+{\Theta }_{13}^{(1)}{x}_3)$
  • $a_2^{(2)}=g({\Theta }_{20}^{(1)}{x}_0+{\Theta }_{21}^{(1)}{x}_1+{\Theta }_{22}^{(1)}{x}_2+{\Theta }_{23}^{(1)}{x}_3)$
  • $a_3^{(2)}=g({\Theta }_{30}^{(1)}{x}_0+{\Theta }_{31}^{(1)}{x}_1+{\Theta }_{32}^{(1)}{x}_2+{\Theta }_{33}^{(1)}{x}_3)$
  • $h_{\Theta }(x)=a_1^{(3)}=g({\Theta }_{10}^{(2)}{a}_0^{(2)}+{\Theta }_{11}^{(2)}{a}_1^{(2)}+{\Theta }_{12}^{(2)}{a}_2^{(2)}+{\Theta }_{13}^{(2)}{a}_3^{(2)})$
  • 可以看出以上计算可以统一归一到一个矩阵的计算，我们可以将其向量化一下
    • Θ ( 1 ) = [ Θ 10 ( 1 ) Θ 11 ( 1 ) Θ 12 ( 1 ) Θ 13 ( 1 ) Θ 20 ( 1 ) Θ 21 ( 1 ) Θ 22 ( 1 ) Θ 23 ( 1 ) Θ 30 ( 1 ) Θ 31 ( 1 ) Θ 32 ( 1 ) Θ 33 ( 1 ) ] ,   X = [ x 0 x 1 x 2 x 3 ] ,   Z ( 2 ) = [ z 1 ( 2 ) z 2 ( 2 ) z 3 ( 2 ) ] ,   A ( 2 ) = [ a 0 ( 2 ) a 1 ( 2 ) a 2 ( 2 ) a 3 ( 2 ) ] \Theta^{(1)}=\begin{bmatrix}\Theta_{10}^{(1)}&\Theta_{11}^{(1)}&\Theta_{12}^{(1)}&\Theta_{13}^{(1)}\\\Theta_{20}^{(1)}&\Theta_{21}^{(1)}&\Theta_{22}^{(1)}&\Theta_{23}^{(1)}\\\Theta_{30}^{(1)}&\Theta_{31}^{(1)}&\Theta_{32}^{(1)}&\Theta_{33}^{(1)}\end{bmatrix},\ X=\begin{bmatrix}x_0\\x_1\\x_2\\x_3\end{bmatrix},\ Z^{(2)}=\begin{bmatrix}z_1^{(2)}\\z_2^{(2)}\\z_3^{(2)}\end{bmatrix},\ A^{(2)}=\begin{bmatrix}a_0^{(2)}\\a_1^{(2)}\\a_2^{(2)}\\a_3^{(2)}\end{bmatrix} Θ(1)= ​Θ10(1)​Θ20(1)​Θ30(1)​​Θ11(<