Description
给定整数N,求1<=x,y<=N且Gcd(x,y)为素数的
数对(x,y)有多少对.
Input
一个整数N
Output
如题
Sample Input
4
Sample Output
4
HINT
hint
对于样例(2,2),(2,4),(3,3),(4,2)
1<=N<=10^7
裸莫比乌斯反演。
设F(n) 为gcd是n的倍数的个数,f(n)为gcd是n的个数,
直接就求 sigma(f(p[i]))就行了,p[i]是质数。
莫比乌斯反演有两种形式,这里我们使用第二种:
一、
二、
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define LL long long
using namespace std;
const int maxn = 1e7 + 10;
int p[maxn/10];
int flag[maxn];
int mu[maxn];
int cnt = 0;
void init()
{
int i,j;
mu[1] = 1;
for(i=2;i<maxn;i++)
{
if(!flag[i])
{
p[cnt++] = i;
mu[i] = -1;
}
for(j=0;j<cnt&&p[j]*i<maxn;j++)
{
flag[p[j]*i] = 1;
if(i % p[j] == 0)
{
mu[p[j]*i] = 0;
break;
}
mu[p[j]*i] = -mu[i];
}
}
}
int main(void)
{
int n,i,j;
init();
while(scanf("%d",&n)==1)
{
LL ans = 0;
for(i=0;i<cnt&&p[i]<=n;i++)
{
LL sum = 0;
for(j=p[i];j<=n;j+=p[i])
{
sum += (LL)mu[j/p[i]]*(n/j)*(n/j);
}
ans += sum;
}
printf("%lld\n",ans);
}
return 0;
}







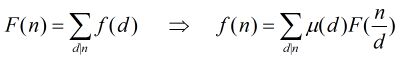
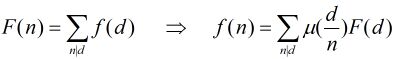














 103
103

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








