L1,L2 正则化:
-
在模型训练的时候,会产生一定的误差。误差其实就是偏差,方差和噪声之和。
-
偏差表示算法的期望与真实值的偏差程度,偏差大通常是因为欠拟合导致的。
-
方差表示数据集的变动导致学习性能的变化,换句话说,就是用来衡量模型在测试集的拟合能力的,方差大通常导致过拟合。
-
噪声则表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界,就是说,模型最好的情况就是放弃拟合那些噪声,但是却拟合了所有正常的特征的意思。
-
用图表表示以上关系:

-
Regularization:就是一种减小方差的策略。为什么要减小方差呢,就是为了降低模型的复杂度,防止过拟合。以下是关于正则化的直观理解。
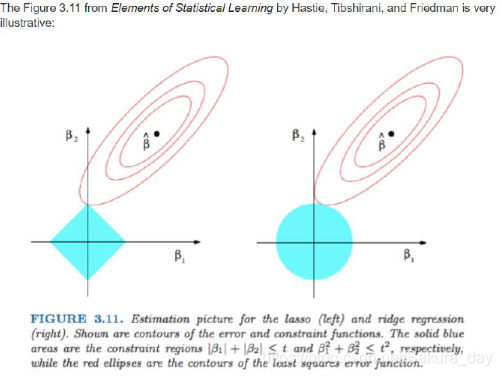
-
从上面正则化可以知道,L1正则化会使得特征变得稀疏,起到了筛选特征,减小模型复杂度的作用。因为Loss的最小值一般在坐标轴上取到,这时候说明其中有一个特征的权重变成0了,从而起到了特征稀疏化的作用。
-
L2正则化会使得模型参数变得更小,而L2正则化有一个别名就是weight_decay。为什么会有这样的作用呢,我们可以从它的反向传播公式看到:
-
w i + 1 = w i − ∂ o b j ∂ w i = w i − ∂ L o s s ∂ w i w_{i+1}=w_{i}-\frac{\partial o b j}{\partial w_{i}}=w_{i}-\frac{\partial L o s s}{\partial w_{i}} wi+1=wi−∂wi∂obj=wi−∂wi∂Loss
w i + 1 = w i − ∂ o b j ∂ w i = w i − ( ∂ L o s s ∂ w i + λ ∗ w i ) w_{i+1}=w_{i}-\frac{\partial o b j}{\partial w_{i}}=w_{i}-\left(\frac{\partial L o s s}{\partial w_{i}}+\lambda * w_{i}\right) wi+1=wi−∂wi∂obj=wi−(∂wi∂Loss+λ∗wi) = w i ( 1 − λ ) − ∂ Loss ∂ w i =w_{i}(1-\lambda)-\frac{\partial \text { Loss }}{\partial w_{i}} =wi(1−λ)−∂wi∂ Loss -
其中有 ( 1 − λ ) (1-\lambda) (1−λ) 的参数,这样使得模型权重缩小了。
-
虽然已经知道了损失函数和代价函数都是些啥,但还是放一下吧,警示一下自己Loss和Cost是两码事,Cost是Loss的取平均:
-
Loss = f ( y ∧ , y ) =f\left(y^{\wedge}, y\right) =f(y∧,y) (损失函数)
-
Cos t = 1 N ∑ i N f ( y i ∧ , y i ) \operatorname{Cos} t=\frac{1}{N} \sum_{i}^{N} f\left(y_{i}^{\wedge}, y_{i}\right) Cost=N1∑iNf(yi∧,yi) (代价函数)
-
Obj = Cost + RegularizationTerm,目标函数等于代价函数和正则化项的和。
-
以下是加了L2正则化和不加的效果图。

使用方法:weight_decay在优化器中实现,可以直接加上这个参数
optim_wdecay = torch.optim.SGD(net_weight_decay.parameters(), lr=lr_init, momentum=0.9, weight_decay=1e-2)
Dropout:
-
Dropout的作用就是神经元的随机失活,这种方法特别适合用在全连接层中。因为全连接层的参数太多,这样会使得模型有过拟合的风险,而且,神经元之间可能会有特别强大的依赖性,可能会导致权重分布不好。
-
Dropout就是在模型训练的时候,让神经元随机失活(通过Dropout Probability控制),失活的神经元权重为0。在模型训练的时候,数据尺度是会有变化的,在测试的时候,全部的神经元都要参与进测试,所以这个时候可以让所有权重乘以(1-drop_prob)。当然在pytorch中的实现细节是,在训练的时候权重都除以(1-p),最后在测试的时候就不用管啦,直接全部神经元拿来测试就可以了。

-
Dropout优势:
- 相当于不同模型的融合,在训练的时候同时训练了多个模型,提高了模型的鲁棒性。
- 能够得到很好的正则化效果:如果随便dropout,神经元对每一个特征都会有平均的关注度,这样就不会使得某一个神经元的w过大。基本上每个神经元权重都是平均分,权重方差就不会偏离太多。
- 和L2正则化的功能相近,能够实现对模型权重的约束
BN,LN,IN,GN
- 知其然之前,要知道其所以然。为什么会出现这么多种N法呢?因为了模型训练的时候会出现ICS现象,就是内部训练变量偏移(Internal Covariate Shift)。比如在原来的文章中说过,如果没有进行合理的初始化,网络在训练的过程中会出现梯度离散的现象,从而使得网络无法训练和使用。这种就是ICS的一种外延。又或者sigmoid用在中间层很容易梯度消失,它的BP=f(x)x(1-f(x))<1/4。不想让梯度消失,就要把数据放在0的左右。
- 为了解决这个问题,研究人员提出了一种方法:BN(Batch Normalization),标准化体现在以下公式中:
- ICS,内部数据分布的偏移,这个是玄学。数据的分布和原来的数据有关,也和激活函数有关
BN层:
-
BN就是减去均值(running_mean),除以方差(running_var)。均值是batch维度上的均值,方差也是。当然输出的output也是需要进行一定的线性变换的。它的γ和β是需要学习的
-
μ B ← 1 m ∑ i = 1 m x i ∥ mini-batch mean σ B 2 ← 1 m ∑ i = 1 m ( x i − μ B ) 2 / / mini-batch variance x ^ i ← x i − μ B σ B 2 + ϵ / / normalize y i ← γ x ^ i + β ≡ B N γ , β ( x i ) ∥ scale and shift \begin{array}{lr}\mu_{\mathcal{B}} \leftarrow \frac{1}{m} \sum_{i=1}^{m} x_{i} & \| \text { mini-batch mean } \\ \sigma_{\mathcal{B}}^{2} \leftarrow \frac{1}{m} \sum_{i=1}^{m}\left(x_{i}-\mu_{\mathcal{B}}\right)^{2} \quad / / \text { mini-batch variance } \\ \widehat{x}_{i} \leftarrow \frac{x_{i}-\mu_{\mathcal{B}}}{\sqrt{\sigma_{B}^{2}+\epsilon}} \quad \quad \quad / / \text { normalize } \\ y_{i} \leftarrow \gamma \widehat{x}_{i}+\beta \equiv \mathrm{BN}_{\gamma, \beta}\left(x_{i}\right) & \| \text { scale and shift }\end{array} μB←m1∑i=1mxiσB2←m1∑i=1m(xi−μB)2// mini-batch variance x i←σB2+ϵxi−μB// normalize yi←γx i+β≡BNγ,β(xi)∥ mini-batch mean ∥ scale and shift

-
计算圈圈中数据的均值和方差。
# BN参数; __init __(self, num_features , eps=1e-5, # 防止除数是0 momentum=0.1, # 指数加权平均估计当前 mean/ var affine=True, # 是不是要仿射变换,就是训练那两个参数啦γ和β track_running_stats= True) # 是训练状态,还是测试状态 -
总之,BN有以下几个优点:1. 可以使用更大的学习率,加快模型的收敛速度。2. 不需要设计权值初始化。3. 不用dropout或者可以使用较小的dropout。4. 不用L2或者用较小的weight decay。5. 直接把LRN淘汰了(AlexNet的过时技术,没有了解)
-
BN其实是一个无心插柳柳成荫的发现,通过它的文章名称就可看出来。它在解决ICS的同时发掘出了一堆有点,这也是当时最重要的发现之一,一直沿用。
-
《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift 》
LN,IN,GN:
- 其实他们的公式和BN基本上是一样的,不一样的就是均值和方差的求取方式。
-
Layer Normalization LN
- 在使用BN的时候发现它并不适用于变长的网络例如(RNN),因为网络神经元个数如果不一样的话,就很难进行BN,BN要求取平均的时候,一个batch中的所有元素的size都是一样的。所以LN计算的是一个Layer里面的那一圈均值和方差。或者说是处理掉CHW这三个维度的均值和方差。和池化的有那么一点感觉

nn.LayerNorm(normalized_shape,eps=1e-5,elementwise_affine=True) # normalized_shape :该层特征形状 - 在使用BN的时候发现它并不适用于变长的网络例如(RNN),因为网络神经元个数如果不一样的话,就很难进行BN,BN要求取平均的时候,一个batch中的所有元素的size都是一样的。所以LN计算的是一个Layer里面的那一圈均值和方差。或者说是处理掉CHW这三个维度的均值和方差。和池化的有那么一点感觉
-
Instance Normalization IN
-
BN 在图像生成( Image Generation )中不适用。你简单地思考一下,如果在进行风格迁移的时候进行归一化,那么会不会把图像的一些纹理特征和某些位置信息给磨平了,它有有着去除图像的对比度信息。
-
所以这个时候就出现了比较奇葩的按照channel进行归一化的操作。用法如下:
nn.InstanceNorm2d(num_features,eps=1e-5,momentum=0.1,affine=False,track_running_stats=False) # num_features :一个样本特征数量(最重要) # momentum :指数加权平均估计当前 mean/ var # track_running_stats:true为训练状态- 图像如下:
-
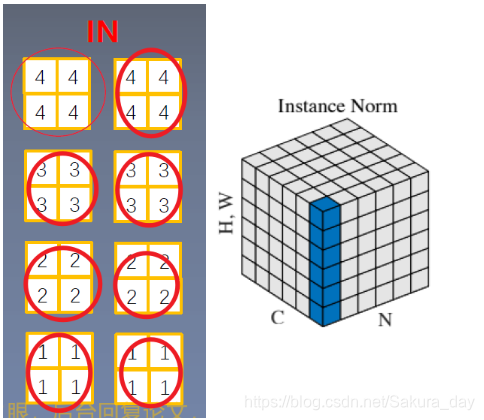
- Group Normalization GN
- 起因:小batch 样本中, BN 估计的值不准。数据不够,通道来凑,把不同feature的通道拿过来用,让样本量大一些,估计的均值和方差准一些。或者换一种方式说,就是做不完全的LN,LN做了一半就是GN。
- 具体的均值和方差的计算方法就按照这些正方体的来看吧。


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








