Luogu P4516 [JSOI2018] 潜入行动

题目描述

外星人又双叒叕要攻打地球了，外星母舰已经向地球航行！这一次，JYY 已经联系好了黄金舰队，打算联合所有 JSOIer 抵御外星人的进攻。

在黄金舰队就位之前，JYY 打算事先了解外星人的进攻计划。现在，携带了监听设备的特工已经秘密潜入了外星人的母舰，准备对外星人的通信实施监听。

外星人的母舰可以看成是一棵 $n$ 个节点、 $n-1$ 条边的无向树，树上的节点用 $1,2,\cdots ,n$ 编号。JYY 的特工已经装备了隐形模块，可以在外星人母舰中不受限制地活动，可以神不知鬼不觉地在节点上安装监听设备。

如果在节点 $u$ 上安装监听设备，则 JYY 能够监听与 $u$ 直接相邻所有的节点的通信。换言之，如果在节点 $u$ 安装监听设备，则对于树中每一条边 $(u,v)$ ，节点 $v$ 都会被监听。特别注意放置在节点 $u$ 的监听设备并不监听 $u$ 本身的通信，这是 JYY 特别为了防止外星人察觉部署的战术。

JYY 的特工一共携带了 $k$ 个监听设备，现在 JYY 想知道，有多少种不同的放置监听设备的方法，能够使得母舰上所有节点的通信都被监听？为了避免浪费，每个节点至多只能安装一个监听设备，且监听设备必须被用完。

输入格式

输入第一行包含两个整数 $n,k$ ，表示母舰节点的数量 $n$ 和监听设备的数量 $k$ 。
接下来 $n-1$ 行，每行两个整数 $u,v$ $(1\le u,v\le n)$，表示树中的一条边。

输出格式

输出一行，表示满足条件的方案数。因为答案可能很大，你只需要输出答案 $\text{mod 1,000,000,007}$ 的余数即可。

样例 #1

样例输入 #1

5 3
1 2
2 3
3 4
4 5

样例输出 #1

1

提示

样例 1 解释

样例数据是一条链 $1-2-3-4-5$ 。首先，节点 $2$ 和 $4$ 必须放置监听设备，否则 $1,5$ 将无法被监听（放置的监听设备无法监听它所在的节点）。剩下一个设备必须放置在 $3$ 号节点以同时监听 $2,4$ 。因此在 $2,3,4$ 节点放置监听设备是唯一合法的方案。

数据范围

存在 $10\%$ 的数据，$1\le n\le 20$ ；

存在另外 $10\%$ 的数据，$1\le n\le 100$ ；

存在另外 $10\%$ 的数据，$1\le k\le 10$ ；

存在另外 $10\%$ 的数据，输入的树保证是一条链；

对于所有数据，$1\le n\le 10^5$​ ， 1 ≤ k ≤ min ⁡ { n , 100 } 1\le k\le \min\{n,100\} 1≤k≤min{n,100} 。

树形dp - 20pts TLE & MLE

明显是一个树形dp。

---

状态定义：

考虑定义$dp(u,i)$表示$u$的子树上（不含$u$）有$i$个监听设备，子树上的点（不含$u$）被全部监听，的方案数。
然而，dp要求无后效性。一个点，除了被儿子，也可以被它的爸爸监听；同时，它也可以监听它的爸爸。对于前者，需要加一维$0/1$表示点$u$是否被儿子监听；对于后者，还要再加一维$0/1$表示点$u$上是否有监听器。
$dp(u,i,0/1,0/1)$.

---

状态转移：

这像是一个树形背包。与$dp(u,i,0/1,0/1),dp(v,j,0/1,0/1)$有关.

在推导状态转移方程时，可以先找一些性质，这样推得轻松些。
显然，不论怎么转移，状态的第三维（点u有没有监听器）一定不会改变。
如果点u没有监听器，它的儿子一定被它儿子的儿子监听。
如果点u不被儿子监听，那么所有儿子都没有监听器。
下面是$i$与$j$的关系：

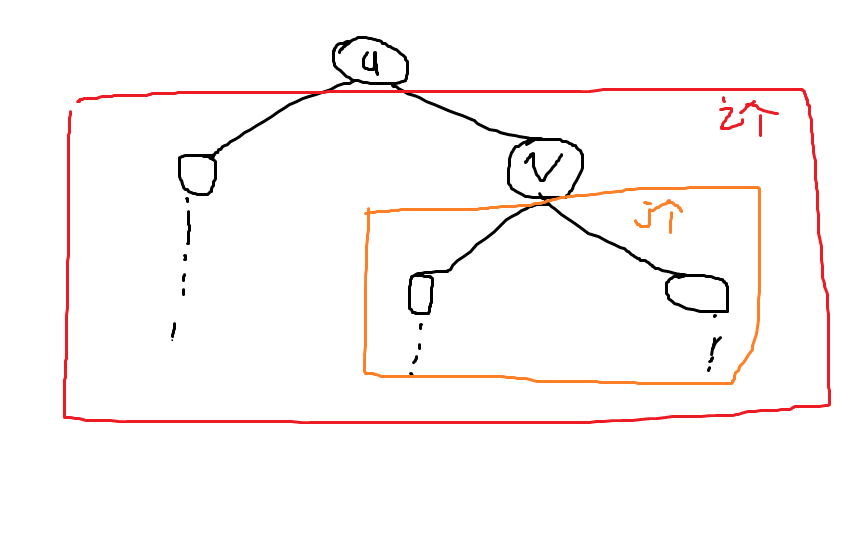
初始化：$dp(u,0,0,0)=dp(u,0,1,0)=1$. 一开始，可以视作只有u一个点。

u没有，不被儿子。儿子全部没有，被儿子的儿子。
$dp(u,i,0,0)+=dp(v,j,0,1)\times dp(u,i-j,0,0)$

u没有，被儿子。儿子被儿子的儿子。
本来就被儿子，加了一个没有的新儿子。$dp(u,i,0,1)+=dp(v,j,0,1)\times dp(u,i-j,0,1)$.
本来随便被不被儿子，反正加了一个有的新儿子。$dp(u,i,0,1)+=dp(v,j,1,1)\times dp(u,i-j-1,0,0/1)$.

另外两种情况同理，以及最终答案，都不再赘述。

注意，这是一个计数类树形背包dp，状态相当于被省去一维。类似于滚动数组，记得转移之前初始化$dp(u,i,0/1,0/1)$为0。
同时，也要注意，由于这题的特殊性，不能直接将它初始化为0，因为转移时会用到长得一样的状态。应该另用一个东西记录$dp(u,i,0/1,0/1)$的结果（万恶啊，卡了我半个多小时）。

---

时间复杂度好像是$O(n{k}^2)$，要超时。
可是我没想到，竟然只能得20pts。

int n, k;
ll dp[MAXN][MAXK][2][2], res[2][2];
vector<int> g[MAXN];

void dfs1(int u, int par) {
	dp[u][0][0][0] = dp[u][0][1][0] = 1;
	for (int v : g[u]) {
		if (v == par) continue;
		dfs1(v, u);
		for (int i = k; i >= 0; --i) {
			memset(res, 0, sizeof(res));
			for (int j = 0; j <= i; ++j) {
				plusmod(res[0][0], mod(dp[v][j][0][1] * dp[u][i - j][0][0]));
				
				plusmod(res[0][1], mod(dp[v][j][0][1] * dp[u][i - j][0][1]));
				if (j < i) plusmod(res[0][1], mod(dp[v][j][1][1] * mod(dp[u][i - j - 1][0][0] + dp[u][i - j - 1][0][1])));
				
				plusmod(res[1][0], mod((dp[v][j][0][0] + dp[v][j][0][1]) * dp[u][i - j][1][0]));
				
				plusmod(res[1][1], mod((dp[v][j][0][0] + dp[v][j][0][1]) * dp[u][i - j][1][1]));
				if (j < i) plusmod(res[1][1], mod(mod(dp[v][j][1][0] + dp[v][j][1][1]) * mod(dp[u][i - j - 1][1][0] + dp[u][i - j - 1][1][1])));
			}
			dp[u][i][0][0] = res[0][0]; dp[u][i][0][1] = res[0][1]; dp[u][i][1][0] = res[1][0]; dp[u][i][1][1] = res[1][1];
		}
	}
}

int main() {
	scanf("%d%d", &n, &k);
	for (int i = 1; i < n; ++i) {
		int a, b; scanf("%d%d", &a, &b);
		g[a].push_back(b); g[b].push_back(a);
	}
	
	dfs1(1, 0);
	printf("%lld\n", dp[1][k][0][1] + dp[1][k - 1][1][1]);
	
	return 0;
}

删除冗余枚举 - 70pts TLE & MLE

对于树形背包dp，一个常规的优化是，
u的子树上只有$siz(u)$个点。$i>siz(u)$的情况显然不用管。
v的子树上只有$siz(v)$个点。$j>siz(v)$的情况显然不用管。

本来以为这个优化力度不大，没想到一下从20pts跳到了70pts。

int n, k, siz[MAXN];
ll dp[MAXN][MAXK][2][2], res[2][2];
vector<int> g[MAXN];

void dfs1(int u, int par) {
	dp[u][0][0][0] = dp[u][0][1][0] = 1;
	for (int v : g[u]) {
		if (v == par) continue;
		dfs1(v, u);
		siz[u] += siz[v] + 1;
		for (int i = min(k, siz[u]); i >= 0; --i) { //这里
			res[0][0] = res[0][1] = res[1][0] = res[1][1] = 0;
			for (int j = 0; j <= min(i, siz[v]); ++j) { //这里
				plusmod(res[0][0], mod(dp[v][j][0][1] * dp[u][i - j][0][0]));
				
				plusmod(res[0][1], mod(dp[v][j][0][1] * dp[u][i - j][0][1]));
				if (j < i) plusmod(res[0][1], mod(dp[v][j][1][1] * mod(dp[u][i - j - 1][0][0] + dp[u][i - j - 1][0][1])));
				
				plusmod(res[1][0], mod((dp[v][j][0][0] + dp[v][j][0][1]) * dp[u][i - j][1][0]));
				
				plusmod(res[1][1], mod((dp[v][j][0][0] + dp[v][j][0][1]) * dp[u][i - j][1][1]));
				if (j < i) plusmod(res[1][1], mod(mod(dp[v][j][1][0] + dp[v][j][1][1]) * mod(dp[u][i - j - 1][1][0] + dp[u][i - j - 1][1][1])));
			}
			dp[u][i][0][0] = res[0][0]; dp[u][i][0][1] = res[0][1]; dp[u][i][1][0] = res[1][0]; dp[u][i][1][1] = res[1][1];
		}
	}
}

int main() {
	scanf("%d%d", &n, &k);
	for (int i = 1; i < n; ++i) {
		int a, b; scanf("%d%d", &a, &b);
		g[a].push_back(b); g[b].push_back(a);
	}
	
	dfs1(1, 0);
	printf("%lld\n", dp[1][k][0][1] + dp[1][k - 1][1][1]);
	
	return 0;
}

把long long改为int - 90pts TLE

仔细算一下空间。用long long存dp数组，$1\times 10^5\times 100\times 4\times 8bytes=305MB$，而内存限制是$250MB$，所以爆空间了。
将long long改为int，变成$153MB$，稳过。但是，由于涉及到两个大int的乘法，又不能改成long long。
这时，我突然想起一年前做一道dp，同样的情况，老杨告诉我，就用int存，但是做乘法时，给它暂时转成long long，然后取模，变成int。
这样，所有的MLE点都没了，只剩一个TLE。

int n, k, siz[MAXN], dp[MAXN][MAXK][2][2], res[2][2];
vector<int> g[MAXN];

void dfs1(int u, int par) {
	dp[u][0][0][0] = dp[u][0][1][0] = 1;
	for (int v : g[u]) {
		if (v == par) continue;
		dfs1(v, u);
		siz[u] += siz[v] + 1;
		for (int i = min(k, siz[u]); i >= 0; --i) {
			res[0][0] = res[0][1] = res[1][0] = res[1][1] = 0;
			for (int j = 0; j <= min(i, siz[v]); ++j) {
				plusmod(res[0][0], mod(1LL * dp[v][j][0][1] * dp[u][i - j][0][0]));
				
				plusmod(res[0][1], mod(1LL * dp[v][j][0][1] * dp[u][i - j][0][1]));
				if (j < i) plusmod(res[0][1], mod(1LL * dp[v][j][1][1] * mod(dp[u][i - j - 1][0][0] + dp[u][i - j - 1][0][1])));
				
				plusmod(res[1][0], mod(1LL * (dp[v][j][0][0] + dp[v][j][0][1]) * dp[u][i - j][1][0]));
				
				plusmod(res[1][1], mod(1LL * (dp[v][j][0][0] + dp[v][j][0][1]) * dp[u][i - j][1][1]));
				if (j < i) plusmod(res[1][1], mod(1LL * mod(dp[v][j][1][0] + dp[v][j][1][1]) * mod(dp[u][i - j - 1][1][0] + dp[u][i - j - 1][1][1])));
			}
			dp[u][i][0][0] = res[0][0]; dp[u][i][0][1] = res[0][1]; dp[u][i][1][0] = res[1][0]; dp[u][i][1][1] = res[1][1];
		}
	}
}

int main() {
	scanf("%d%d", &n, &k);
	for (int i = 1; i < n; ++i) {
		int a, b; scanf("%d%d", &a, &b);
		g[a].push_back(b); g[b].push_back(a);
	}
	
	dfs1(1, 0);
	printf("%d\n", mod(dp[1][k][0][1] + dp[1][k - 1][1][1]));
	
	return 0;
}

进一步删除冗余枚举 - AC（补）

接下来，我试了各种卡常方法，开了O2，都无法改变那个TLE。在题解区翻了半天，也没找到什么方法。很多题解用的是刷表法，难道会比我的查表法快些？但我懒得重新写。

直到我在讨论版里找到一个解决方案。
在“删除冗余状态”子标题中，我只考虑了u的子树大小，v的子树大小。事实上，还要考虑转移前u原来的子树的大小，即须$i-j-1\le siz(u),j\ge i-1-siz(u)$，这里$siz[u]$是原来的子树大小。

int n, k, siz[MAXN], dp[MAXN][MAXK][2][2], res[2][2];
vector<int> g[MAXN];

void dfs1(int u, int par) {
	dp[u][0][0][0] = dp[u][0][1][0] = 1;
	for (int v : g[u]) {
		if (v == par) continue;
		dfs1(v, u);
		for (int i = min(k, siz[u] + siz[v] + 1); i >= 0; --i) {
			res[0][0] = res[0][1] = res[1][0] = res[1][1] = 0;
			for (int j = max(0, i - 1 - siz[u]); j <= min(i, siz[v]); ++j) { //这里
				plusmod(res[0][0], mod(1LL * dp[v][j][0][1] * dp[u][i - j][0][0]));
				
				plusmod(res[0][1], mod(1LL * dp[v][j][0][1] * dp[u][i - j][0][1]));
				if (j < i) plusmod(res[0][1], mod(1LL * dp[v][j][1][1] * mod(dp[u][i - j - 1][0][0] + dp[u][i - j - 1][0][1])));
				
				plusmod(res[1][0], mod(1LL * (dp[v][j][0][0] + dp[v][j][0][1]) * dp[u][i - j][1][0]));
				
				plusmod(res[1][1], mod(1LL * (dp[v][j][0][0] + dp[v][j][0][1]) * dp[u][i - j][1][1]));
				if (j < i) plusmod(res[1][1], mod(1LL * mod(dp[v][j][1][0] + dp[v][j][1][1]) * mod(dp[u][i - j - 1][1][0] + dp[u][i - j - 1][1][1])));
			}
			dp[u][i][0][0] = res[0][0]; dp[u][i][0][1] = res[0][1]; dp[u][i][1][0] = res[1][0]; dp[u][i][1][1] = res[1][1];
		}
		siz[u] += siz[v] + 1;
	}

关于时间复杂度（补）

第一反应是$O(n{k}^2)$。事实上，是$O(nk)$，稳过的。
用子树合并来看待树形背包dp。出现$k^2$枚举，是两棵大小为k的子树合并。这种合并最多出现$n/k$次。所以时间复杂度是$O(nk)$.

总结

这题倒是简单的，套路的，但状态转移有些麻烦。过程中也暴露出了很多关于dp常见的，我却不熟悉的技巧。
我几乎花了一整个晚自习。要是能在考场上流畅地做出来，也是一个本事吧。