关联规则与购物篮分析实战

导读：本文介绍了关联规则原理及Apriori算法实现购物篮分析，以一个真实案例辅助理解关联分析。

背景与需求

客户A企业是一家全球知名家具和家居零售商，销售主要包括座椅/沙发系列、办公用品、卧室系列、厨房系列、照明系列、纺织品、炊具系列、房屋储藏系列、儿童产品系列等约10,000个产品。为了维持顾客忠诚度、扩大销售，A企业希望通过顾客已有的购买记录，为顾客推荐更多的产品。请使用关联规则的方法，实现客户的需求。

相关数据

purchase.csv存放的顾客交易记录，RA_desc.csv为商品小类编号对应的含义，PA_desc.csv为商品大类编号对应的含义。本案例只涉及到顾客交易记录，因此purchase.csv说明如下：

1. 商品编号代表具体的商品，每个商品都有自己的归类——商品小类和商品大类，商品大类包含商品小类；例如，商品编号为40165961是一款“28x28 厘米灰色煎锅”，其商品小类为141，即Cookware，其商品大类为14，即Cooking

2. 表purchase.csv每一行为一个顾客（主卡）购买一种商品（商品编号）的交易记录；

3. POS.ID为店内POS收银机的编号

4. 主卡为会员卡号

5. 小票序号该商品在小票上的序号

6. 其他字段意义明确，不做赘述。

数据已经整理好：

链接：https://pan.baidu.com/s/19FxrfCxnqRaznlyxFetreA 

提取码：niub 

理论基础

什么是购物篮分析

单个客户一次购买商品的总和称为一个购物篮。其思想是分析商品与商品之间的关联（如经典啤酒和尿布）。

常用算法分为两种：不考虑购物顺序的关联规则；以及考虑购物顺序的序贯模型。

购物蓝分析主要应用于超市货架布局、互补品与互斥品、套餐设计和捆绑销售。

关联规则的概念

是n个不同项目的集合， 称为一个项目(item)

项目的集合称为项目集合(Itemset)，简称为项集。其元素个数称为项集的长度，长度为 的项集称为 (k-Itemset)

每笔交易 (Transaction)是项集 上的一个子集，即 

交易的全体构成了交易记录集 ，简称交易集 ，交易集 中 包含交易的个数记为

设A，B为两个项集，则关联规则是如下蕴涵式
 ，其中 ,  ,且

支持度和置信度

对于关联规则 ，定义如下两个指标

支持度

是两件商品 在总销售笔数(N)中出现的概率， 即   与   同时被购买的概率。

支持度表示规则是否普遍。

置信度

置信度是一种条件概率， 表示购买了A后再购买B的概率。

一个小例子计算支持度和置信度

有如下五个购物篮，每个购物篮中分别标明了商品标签，现根据规则计算支持度及置信度。

根据支持度

规则	支持度	置信度
A => D	2/5	2/3
C => A	2/5	2/4
A => C	2/5	2/3
B&C=>D	1/5	1/3

提升度

提升度表示先购买 对购买 的概率的提升作用。

提升度是两种可能性的比较，一种是在已知购买了左边商品情况下购买右边商品的可能性，另一种是任意情况下购买右边商品的可能性。

只有提升度(A->B)的值大于1才说明关联规则真正有效，说明物品A卖得越多，B也会卖得越多。而提升度等于1则意味着产品A和B之间没有关联。最后，提升度小于1那么意味着购买A反而会减少B的销量

此外， 和 的提升度是一样的。

关联规则挖掘

关联规则挖掘的定义：给定一个交易数据集T，找出其中所有支持度和置信度满足一定条件的关联规则。最简单的方法是穷举项集的所有组合，并计算和判断每个组合是否满足条件，一个长度为n的项集的组合个数是？

怎样快速挖出满足条件的关联规则是关联挖掘的需要解决的主要问题。Apriori算法是解决这一问题的最流行的算法。

Apriori算法

生成频繁项集

这一阶段找出所有满足最小支持度的项集，找出的这些项集称为频繁项集。

Apriori基于以下两条核心原理生成频繁项集：

• 如果某个项集是频繁的，那么它的所有子集也是频繁的。

• 若子集不是频繁的，则所有包含它的项集都是不频繁的。

运用Apriori算法的思想，我们就能去掉很多非频繁的项集，大大简化计算量。

生成规则

在上一步产生的频繁项集的基础上生成满足最小置信度的规则，产生的规则称为强规则。

关联规则挖掘所花费的时间主要是在生成频繁项集上，因为找出的频繁项集往往不会很多，利用频繁项集生成规则也就不会花太多的时间。

Apriori算法步骤

第一步:所有单独的项都是候选项集 C1，任何支持度比给定的最小支持度小的项都将从候选项集 C1中剔除，形成频繁 1-项集 L1

连接步:两个 L1通过自连接形成具有 2 个项的候选项集C2

剪枝步:通过再次扫描交易集决定这些候选项的支持度，保留比预先给定的最小支持度大的候选项，形成频繁2-项集L2

最后一步:形成含有 3 个项的候选项集 C3，重复上述步骤，直到找到所有的频繁项集为止。

Apriori算法优缺点

Apriori算法利用频繁集的两个特性，过滤了很多无关的集合，效率提高不少。

Apriori算法是一个候选消除算法，每一次消除都需要扫描一次所有数据记录，造成整个算法在面临大数据集时显得无能为力。每次生成频繁项集时都要进行全表扫描。

项目实战

使用mlxtend.frequent_patterns实现关联规则，需要安装并导入库：

pip install mlxtend
from mlxtend.frequent_patterns import apriori, association_rules

数据预处理

pd.read_csv('./purchase.csv',sep=',',
            header=0,encoding="gbk")

思考：在建模之前，需要先对数据进行处理，思考如何定义购物篮，使用哪些字段？

这里我们定义三个字段，两个原有字段：交易号、商品大类，一个衍射字段：交易次数（times）

col1 = '交易号'
col2 = '商品大类'
col3 = 'times'
purchase_df.pivot_table(index=col1,
                        columns=col2,
                        values=col3)

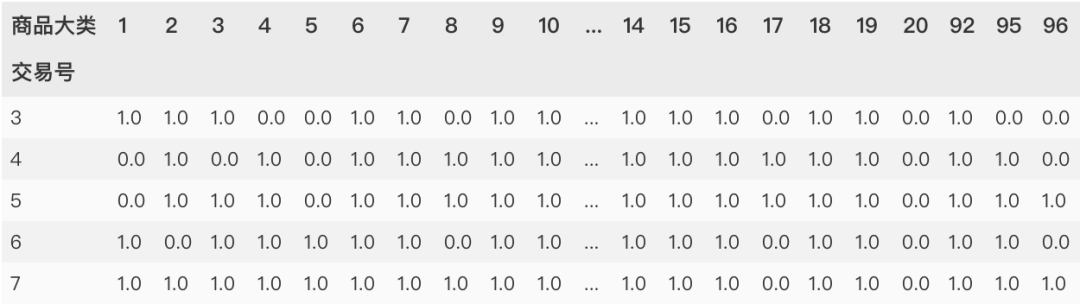
求频繁项集并排序

我们设定的最小支持度是0.6，那么只有支持度大于0.6的物品集合才是频繁项集。

frequent_itemsets = apriori(traction,
              min_support=0.6,
              use_colnames=True,
              max_len=None)
frequent_itemsets.sort_values(by='support',
                              ascending=False,
                              inplace=True) 

参数

df：数据集。
min_support：给定的最小支持度。
use_colnames：默认False，则返回的物品组合用编号显示，为True的话直接显示物品名称。
max_len：最大物品组合数，默认是None，不做限制。如果只需要计算两个物品组合的话，便将这个值设置为2。

	support	itemsets
5	0.685714	(14)
8	0.680672	(18)
...	...	...

求关联规则

我们前面已经用Apriori得到频繁项集了。那么我们就可以在频繁项集的基础上，找到这里面的关联规则。而计算关联规则所用到的，就是我们上面所说的置信度和提升度。

这里有一点要注意，当我们发现置信度(A->B)很高的时候，反过来的值置信度(B->A)不一定很高。

association_rule = association_rules(
                   frequent_itemsets,
                   metric='confidence',
                   min_threshold=0.5)
association_rule.sort_values(
                  by='confidence',
                  ascending=False,
                  inplace=True)    
# 关联规则可以按leverage排序

参数

df：就是 Apriori 计算后的频繁项集。

metric：可选值 ['support','confidence','lift','leverage','conviction'] 里面比较常用的就是置信度和支持度。这个参数和下面的min_threshold参数配合使用。

min_threshold：参数类型是浮点型，根据 metric 不同可选值有不同的范围，
metric = 'support' 取值范围 [0,1]
metric = 'confidence' 取值范围 [0,1]
metric = 'lift' 取值范围 [0, inf]

support_only：默认是 False。仅计算有支持度的项集，若缺失支持度则用 NaNs 填充。

上表字段含义

antecedents：规则先导项
consequents：规则后继项
antecedent support：规则先导项支持度
consequent support：规则后继项支持度
support：规则支持度 （前项后项并集的支持度）
confidence：规则置信度 （规则置信度：规则支持度support / 规则先导项）
lift：规则提升度，表示含有先导项条件下同时含有后继项的概率，与后继项总体发生的概率之比。一般大于1才有意义

• lift(A->C) = confidence(A->C) / support(C) range: [0, inf]

leverage：Leverage=0时A和C独立，Leverage越大A和C的关系越密切

• leverage(A->C) = support(A->C) - support(A)*support(C), range: [-1, 1]

conviction：这个值越大, A、C越关联。

• conviction = [1 - support(C)] / [1 - confidence(A->C)], range: [0, inf]

上面例子中我们可以发现，{18,11 -> 15} 的置信度是 0.99449 ，而它们的提升度是 1.468292。这说明买了{18,11}的人很可能会再购买 1.468 份的 15 。所以可以让它们放到一起出售。

OK，相信通过本次案例，已经能够明白Apriori算法的原理以及如何使用它。当然Apriori只能算是关联挖掘算法中比较基础的一个，还有其他的关联挖掘算法，比如FP-growth，等等。