特征工程分析

1 特征工程是什么？
　　有这么一句话在业界广泛流传：数据和特征决定了机器学习的上限，而模型和算法只是逼近这个上限而已。那特征工程到底是什么呢？顾名思义，其本质是一项工程活动，目的是最大限度地从原始数据中提取特征以供算法和模型使用。
　　
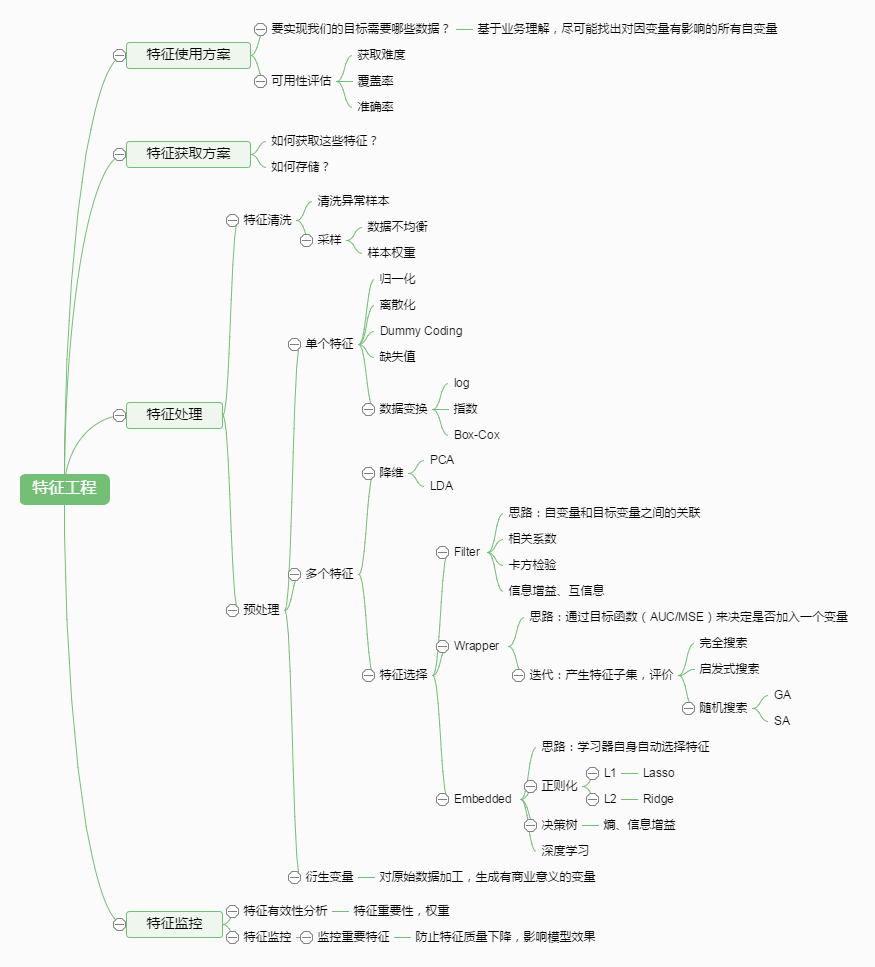
　　特征处理是特征工程的核心部分，sklearn提供了较为完整的特征处理方法，包括数据预处理，特征选择，降维等。首次接触到sklearn，通常会被其丰富且方便的算法模型库吸引，但是这里介绍的特征处理库也十分强大！
2 数据预处理
　　通过特征提取，我们能得到未经处理的特征，这时的特征可能有以下问题：
不属于同一量纲：即特征的规格不一样，不能够放在一起比较。无量纲化可以解决这一问题。
信息冗余：对于某些定量特征，其包含的有效信息为区间划分，例如学习成绩，假若只关心“及格”或不“及格”，那么需要将定量的考分，转换成“1”和“0”表示及格和未及格。二值化可以解决这一问题。
定性特征不能直接使用：某些机器学习算法和模型只能接受定量特征的输入，那么需要将定性特征转换为定量特征。最简单的方式是为每一种定性值指定一个定量值，但是这种方式过于灵活，增加了调参的工作。通常使用哑编码的方式将定性特征转换为定量特征：假设有N种定性值，则将这一个特征扩展为N种特征，当原始特征值为第i种定性值时，第i个扩展特征赋值为1，其他扩展特征赋值为0。哑编码的方式相比直接指定的方式，不用增加调参的工作，对于线性模型来说，使用哑编码后的特征可达到非线性的效果。
存在缺失值：缺失值需要补充。
信息利用率低：不同的机器学习算法和模型对数据中信息的利用是不同的，之前提到在线性模型中，使用对定性特征哑编码可以达到非线性的效果。类似地，对定量变量多项式化，或者进行其他的转换，都能达到非线性的效果。
　　我们使用sklearn中的preproccessing库来进行数据预处理，可以覆盖以上问题的解决方案。
　　类 功能 说明
StandardScaler 无量纲化 标准化，基于特征矩阵的列，将特征值转换至服从标准正态分布
MinMaxScaler 无量纲化 区间缩放，基于最大最小值，将特征值转换到[0, 1]区间上
Normalizer 归一化 基于特征矩阵的行，将样本向量转换为“单位向量”
Binarizer 二值化 基于给定阈值，将定量特征按阈值划分
OneHotEncoder 哑编码 将定性数据编码为定量数据
Imputer 缺失值计算 计算缺失值，缺失值可填充为均值等
PolynomialFeatures 多项式数据转换 多项式数据转换
FunctionTransformer 自定义单元数据转换 使用单变元的函数来转换数据
3 特征选择
　　当数据预处理完成后，我们需要选择有意义的特征输入机器学习的算法和模型进行训练。通常来说，从两个方面考虑来选择特征：

特征是否发散：如果一个特征不发散，例如方差接近于0，也就是说样本在这个特征上基本上没有差异，这个特征对于样本的区分并没有什么用。
特征与目标的相关性：这点比较显见，与目标相关性高的特征，应当优选选择。除方差法外，本文介绍的其他方法均从相关性考虑。
　　根据特征选择的形式又可以将特征选择方法分为3种：

Filter：过滤法，按照发散性或者相关性对各个特征进行评分，设定阈值或者待选择阈值的个数，选择特征。
Wrapper：包装法，根据目标函数（通常是预测效果评分），每次选择若干特征，或者排除若干特征。
Embedded：嵌入法，先使用某些机器学习的算法和模型进行训练，得到各个特征的权值系数，根据系数从大到小选择特征。类似于Filter方法，但是是通过训练来确定特征的优劣。
　　我们使用sklearn中的feature_selection库来进行特征选择。
　　类 所属方式 说明
VarianceThreshold Filter 方差选择法
SelectKBest Filter 可选关联系数、卡方校验、最大信息系数作为得分计算的方法
RFE Wrapper 递归地训练基模型，将权值系数较小的特征从特征集合中消除
SelectFromModel Embedded 训练基模型，选择权值系数较高的特征
4 降维
　　当特征选择完成后，可以直接训练模型了，但是可能由于特征矩阵过大，导致计算量大，训练时间长的问题，因此降低特征矩阵维度也是必不可少的。常见的降维方法除了以上提到的基于L1惩罚项的模型以外，另外还有主成分分析法（PCA）和线性判别分析（LDA），线性判别分析本身也是一个分类模型。PCA和LDA有很多的相似点，其本质是要将原始的样本映射到维度更低的样本空间中，但是PCA和LDA的映射目标不一样：PCA是为了让映射后的样本具有最大的发散性；而LDA是为了让映射后的样本有最好的分类性能。所以说PCA是一种无监督的降维方法，而LDA是一种有监督的降维方法。
　　库 类 说明
decomposition PCA 主成分分析法
lda LDA 线性判别分析法